В настоящей статье в развитие работ [1; 2] обсуждается реакция
![]() ,
,
которая привлекает особое внимание, если темная материя содержит нейтринную компоненту. Аннигиляция пары электронных нейтрино в пару мюонных может наблюдаться параллельно с нейтринными осцилляциями солнечных нейтрино, которые впервые обсуждались в работе [3]. Наблюдение таких осцилляций [4] означало, что массы нейтрино отличны от нуля. В этом можно убедиться, исследуя модель, предложенную для К-мезонов [5], или следуя работе [6]. Считая в случае 2-х ароматов (![]() и
и ![]() ), что
), что
![]()
или
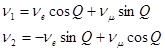 ,
,
где ![]() соответствуют состояниям с массами
соответствуют состояниям с массами ![]() и
и ![]()
![]() , а Q – угол смещения. Получаем, что если в момент t=0 рождено
, а Q – угол смещения. Получаем, что если в момент t=0 рождено ![]()
![]()
то в произвольный момент t
![]()
где ![]() ,
, ![]() .
.
Вероятность обнаружить в потоке ![]() примесь
примесь ![]() на расстоянии Z:
на расстоянии Z:
![]()
То есть вероятность появления нейтрино с другими ароматами является осциллирующей функцией пройденного расстояния, а наблюдение осцилляций означает, что m1 и m2 не равны.
В рамках стандартной модели [7] нейтрино должны быть безмассовыми. Экспериментальные ограничения на массы нейтрино довольно жесткие [6]:
![]()
![]() ,
,
однако ситуация с нейтрино вызывает много вопросов. Например, остаются необъясненными результаты по измерению скорости ![]() , оказавшейся больше скорости света [8], проблемы с углом смешивания, сезонные вариации потока нейтрино.
, оказавшейся больше скорости света [8], проблемы с углом смешивания, сезонные вариации потока нейтрино.
Возможное присутствие нейтринной компоненты в темной материи вызывает естественный интерес к процессу нейтринной аннигиляции, так как порог реакции для обсуждаемой реакции невысок, если масса нейтрино невелика и в системе центра инерции.
![]()
Для расчета сечения реакции воспользуемся результатами работы [1] для локального взаимодействия или результатами [2] при учете конкретной динамики процесса (через z-бозон). В локальном пределе (при малых энергиях этого достаточно) в 4-мерном виде получаем общее выражение для квадрата модуля матричного элемента ![]() при учете масс и поляризаций всех частиц:
при учете масс и поляризаций всех частиц:
![]()
![]()
![]()
![]()
где qi – 4-х импульсы частицы; mi – массы нейтрино; Si – 4-х спины соответствующих частиц.
Учитывая конкретную динамику процесса (через z -озон):
![]() ,
,
получаем результат как частный случай работы [3], однако при малых энергиях все сводится к замене G2 на ![]() , где mz – масса z – бозона, а qz – 4-х импульс z-бозона.
, где mz – масса z – бозона, а qz – 4-х импульс z-бозона.
Для оценки поляризационных корреляций необходимо прейти к 3-мерной форме. Однако общий случай слишком громоздок, поэтому приведем результат для 3 частных случаев.
При учете поляризаций начальных частиц в СЦИ
![]()
![]() ,
,
где ![]() – 3-х импульс
– 3-х импульс ![]() ;
; ![]() – 3-х импульс
– 3-х импульс ![]() ;
; ![]() – энергия нейтрино;
– энергия нейтрино; ![]() и
и ![]() – 3-мерные векторы поляризации
– 3-мерные векторы поляризации ![]() и
и ![]() .
.
Аналогично при учете поляризаций конечных нейтрино.
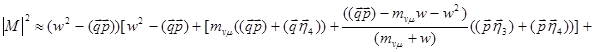
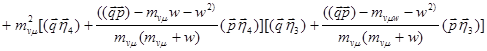 ,
,
где оставлены прежние обозначения, а ![]() и
и ![]() – 3-х импульсы
– 3-х импульсы ![]() и
и ![]() .
.
Учитывая поляризации ![]() и
и ![]() , имеем
, имеем
![]()
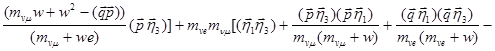
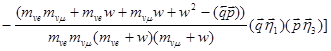 ,
,
где все обозначения прежние.
Для вычисления сечения используем методику [5]:
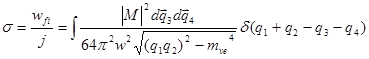
Где j – плотность потока; wfi – вероятность перехода в единицу времени; ![]() 4-мерная
4-мерная ![]() – функция Дирака.
– функция Дирака.
Из определения сечения получается, что вероятность реакции пропорциональна числу ![]() , падающих на площадь 1 м2 за 1 с и концентрации
, падающих на площадь 1 м2 за 1 с и концентрации ![]() в темной материи. В отличие от случая осцилляций, вероятность такой реакции пропорциональна пройденному расстоянию.
в темной материи. В отличие от случая осцилляций, вероятность такой реакции пропорциональна пройденному расстоянию.
При интегрировании по ![]() -функции, следуя методике работы [5] при учете массы
-функции, следуя методике работы [5] при учете массы ![]() , получаем:
, получаем:
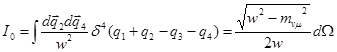 ,
,
где ![]() элемент телесного угла (в сферической системе координат). В случае
элемент телесного угла (в сферической системе координат). В случае ![]() естественно результат совпадает с [5], т.е.
естественно результат совпадает с [5], т.е. ![]() .
.
При вычислении сечения необходимо использовать интеграл [5]
![]()
Где 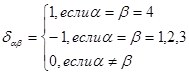
![]() симметричный тензор второго ранга.
симметричный тензор второго ранга.
В этой формуле q=q1+q2
При учете масс нейтрино
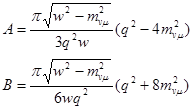 ,
,
что совпадает с результатами [5], если массы нейтрино равны 0.
Для полного сечения получаем в общем 4-мерном виде:
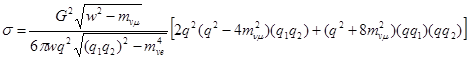
Переход к 3-мерной форме стандартный и, поскольку ввиду трудностей экспериментальной проверки выбор системы отсчета (ЛС – лабораторная система отсчета или СЦИ – система центра инерции) не очевиден, приводить его преждевременно.
При проведении интегрирования возможен и другой вариант [9]:
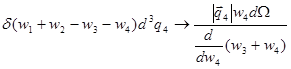
Полученные результаты соответствуют случаю, когда нейтрино является нормальными частицами. Если подтвердится информация о том, что скорости нейтрино выше скорости света [8], то возможно, понадобится корректировка полученных формул, так как общепризнанных теорий тахионов, по-видимому, нет.
Выражение для вероятности и поляризационных корреляций является достаточно общим, но в основном они представляют теоретический интерес, так как экспериментальная проверка является сложной.
Рецензенты:
Рогозин Валентин Дмитриевич, д.т.н., профессор кафедры «Материаловедение и композиционные материалы» Волгоградского государственного технического университета, г. Волгоград.
Шеин Александр Георгиевич, д.ф-м.н., профессор, заведующий кафедрой «Физика» Волгоградского государственного технического университета, г. Волгоград.
Криштоп Виктор Владимирович, д.ф.м.н., профессор, заведующий кафедрой «Физика», Дальневосточный государственный университет путей сообщения, г. Хабаровск, профессор Kwangmoon University, Korea.
Библиографическая ссылка
Гнедов Ю.А., Казак В.Ф., Юрьева С.А. К ВОПРОСУ ОБ ОСЦИЛЛЯЦИЯХ НЕЙТРИНО // Современные проблемы науки и образования. 2012. № 6. ;URL: https://science-education.ru/ru/article/view?id=7809 (дата обращения: 20.12.2025).



