Прочность деталей молота, качественные показатели этой машины зависят от силы сопротивления поковки деформированию. У каждого молота существует предельная поковка, при которой долговечность слабейшего звена (штока) оказывается неудовлетворительной. Шток постоянного сечения весьма далек от равнопрочного состояния, поскольку работает в условиях больших ударных нагрузок, испытывая при ударе напряжение от продольных сил. В месте заделки штока в бабу одновременно действуют два неблагоприятных фактора: возникает максимальное динамическое напряжение и имеет место наибольшая концентрация напряжений. В итоге подавляющее число поломок таких штоков происходит в одном и том же сечении – в заделке [4].
В настоящее время в машиностроении используются штоки ковочных молотов, имеющие сплошное поперечное сечение согласно ГОСТ 9752-75 (рис. 1).
Рис. 1.
Недостатком этой конструкции является недостаточная надежность и долговечность штока в месте его заделки в бабу. В данной работе предлагается новая конструкции штока с полостями переменного сечения, например цилиндрическими отверстиями ступенчато-переменного сечения, начинающимися от концевого участка штока со стороны, противоположной месту заделки штока в бабу (рис. 2).
Рис. 2.
Предлагаемая конструкция штока позволяет снизить нагрузки, возникающие в месте заделки штока в бабу, и направлена на повышение надежности штоков, что позволяет увеличить срок их эксплуатации и тем самым сократить материальные потери от замены штоков и от простоя оборудования в период их замены. Снижение напряжений достигается за счет перераспределения напряжений при ударном воздействии в различных сечениях штока. Этот эффект получен в результате частотного метода расчета ковочного молота в процессе ударного взаимодействия с заготовкой.
Рассмотрим для примера паровоздушный ковочный молот арочного типа модели М1345 (рис. 3).
На рис. 3. представлена принципиальная расчетная схема молота, позволяющая проводить вариантные расчеты в случае существующей и предлагаемой конструкции штока, где участки 7-8, 12-13, 14-15 моделируют стыки, узлы 17, 18, 19 моделируют упругое основание.
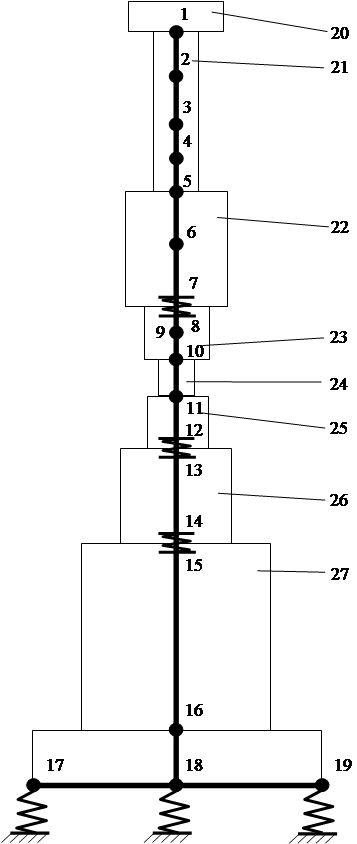
Рис. 3.
Рассмотрим частотный метод динамического расчета нестационарных колебаний ковочного молота в процессе ударного взаимодействия с заготовкой. Предлагаемая методика использует модификацию метода конечных элементов (МКЭ), основанную на точном интегрировании дифференциального уравнения для конечного элемента [2], и позволяет рассчитывать продольные и поперечные колебания стержней ступенчато-переменного сечения с учетом или без учета рассеяния энергии при соударении с жестким препятствием [3; 5].
Предлагаемый подход справедлив для стержней неограниченной длины, поэтому разбиение на участки молота можно проводить в любых сечениях, но наиболее целесообразно там, где меняются физические или геометрические характеристики объекта. При составлении расчетной схемы молота считалось, что в штоке, бабе, бойках, подушке и верхней части шабота возникают продольные колебания, а в основании шабота – поперечные.
Предлагаемой расчетной схеме (рис. 3) соответствует следующая система разрешающих уравнений для построения амплитудно-фазо-частотных характеристик (АФЧХ) перемещений:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
,
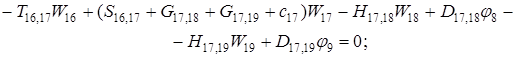
где:
, 
;
; 
;
;
; 
;
; 
; 
; 
;
;
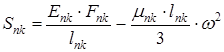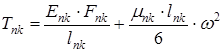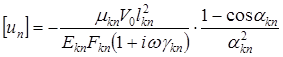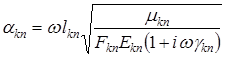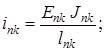
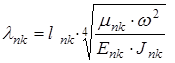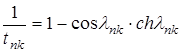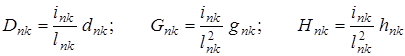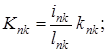
n, k – индексы, указывающие соответственно на начало и конец участка;
j – номер узла (i = 1, 2… 19);
i – мнимая единица, 
;
Jnk – осевой момент инерции сечения участка nk, м4;
Еnk – модуль упругости участка nk, Па;
Fnk – площадь поперечного сечения участка nk, м2;
lnk – длина участка nk, м;
m nk – масса единицы длины стержня участка nk, 
;
V0 – скорость соударения с заготовкой, м/с;
– коэффициент сопротивления участка nk.
– частота колебаний, с-1;
Wj – перемещение j-го узла, м;
j j – угол поворота j-го узла, рад;
сj – жесткости пружин, моделирующих упругое основание в jом узле, ;
сnk – жесткости пружин, моделирующих стыки nk, .
Из этой системы находятся изображения перемещений в узлах системы. Зная перемещения начала и конца стержня, рассчитываются продольные усилия Ni(). Переходя к оригиналам N(t), находятся напряжения 
и деформации 
, которые связаны с усилиями следующими зависимостями:
; 
,
где: – напряжение, Па;
– продольная сила, Н;
t – время, с;
– деформации, м;
F – площадь поперечного сечения, м2;
Е – модуль упругости, Па.
Установлено, что максимальные напряжения, в несколько раз превышающие напряжения в других узлах системы, возникают в месте заделки штока в бабу (5 узел рис. 3), что подтверждает предварительные сведения из практики о подавляющем числе поломок именно в этом сечении.
Предлагается следующий путь уменьшения нагрузок, возникающих в месте заделки штока в бабу. Можно распределить нагрузку на несколько сечений. Для этого следует в качестве новой конструкции штока использовать шток с цилиндрическими отверстиями ступенчато-переменного сечения (рис. 2).
При динамическом анализе конструкции с таким штоком получили снижение напряжений в 3 узле на 15% в случае стальной заготовки и на 16% – в случае алюминиевой.
Это достигается за счет перераспределения напряжений во 2, 3, 4 и 5 узлах. Так, при использовании предлагаемой конструкции штока напряжение в проблемном 5 сечении уменьшается с 31,2 до 27,5 МПа в случае стальной заготовки и с 20,3 до 17 МПа в случае алюминиевой. А во втором и третьем узлах напряжение увеличивается приблизительно в три и два раза соответственно, что незначительно по сравнению с напряжением в 5 узле. При этом наблюдается снижение напряжений на 5–6% в остальных узлах системы (рис. 4).
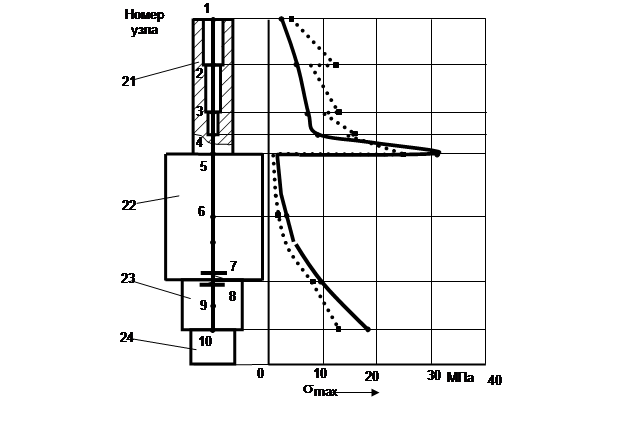
Рис. 4.
Предлагаемые изменения в конструкции штока снижают возникающие в месте заделки штока в бабу напряжения на (18–20)% и направлены на повышение надежности штоков, что позволяет увеличить срок их эксплуатации и тем самым сократить материальные потери от замены штоков и от простоя оборудования в период их замены.
Результаты сравнения теоретических и экспериментальных результатов в случае молота со штоком постоянного сечения показали, что средняя погрешность вычислений составляет 14% для частот собственных колебаний и 25% для амплитуд колебаний [1].
Рецензенты:
Лебедев А.М., доктор технических наук, доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск.
Дмитриенко Г.В., доктор технических наук, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск.
Библиографическая ссылка
Санкин Ю.Н., Юганова Н.А. ШТОК КОВОЧНОГО МОЛОТА С ОТВЕРСТИЯМИ СТУПЕНЧАТО-ПЕРЕМЕННОГО СЕЧЕНИЯ // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7499 (дата обращения: 16.04.2024).