Данная работа посвящена разработке методики расчета трехмерных течений вязкого газа на блочно-структурированных эйлеровых сетках с использованием существенно неосциллирующих схем повышенного порядка точности [6]. Методика ориентирована на решение внутренних и внешних задач аэродинамики и является развитием методик, применяемых в пакете программ ЛОГОС [2].
Для описания расчетных методик запишем систему уравнений Навье-Стокса и уравнения модели турбулентности в декартовых координатах в векторном виде:
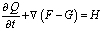. (1)
Здесь,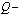 
вектор консервативных переменных, 
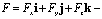вектор конвективных потоков, 
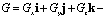вектор вязких потоков.
Поскольку в данной работе рассматриваются алгоритмы на структурированных сетках, то при описании алгоритмов расчета будем использовать следующее обозначение: текущую ячейку будем обозначать индексом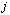 
, левые и правые грани ячейки относительно рассматриваемой переменной по направлениям 
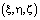индексам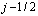и 
и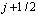 
соответственно. При этом направление нормалей на гранях соответствует возрастанию переменной.
Точность получаемых решений во многом зависит от способа вычисления конвективных потоков. Использование блочно-структурированных сеток позволяет осуществлять реконструкции решения на гранях ячеек повышенного порядка точности: линейная, квадратичная и кубическая реконструкции. Эти реконструкции и описание методик расчета на блочно-структурированных сетках приводится в работе [1].
Рассмотрим подробнее одномерную ENO-реконструкцию. Пусть дана сетка
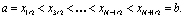
Обозначим ячейки, их центры и шаг сетки
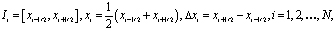
соответственно. Обозначим
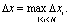
Предположим, что в ячейках заданы средние значения некоторой функции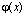
:
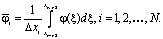
Построим полином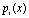
степени не больше
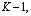который аппроксимирует функцию
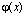с порядком точности
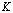в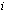 
-й ячейке:
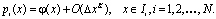
Таким образом, можно восстановить значения функции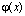
на границе ячейкис порядком точности
:
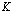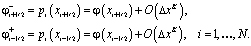
Рассмотрим ячейку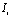
и «шаблон» состоящий из
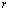ячеек слева и
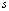ячеек справа от этой ячейки и самой ячейки
:
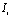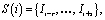
где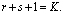
Существует единственный полином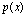
степени не больше
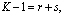который удовлетворяет условию
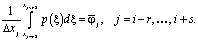
Искомый полином запишется в виде [6]:
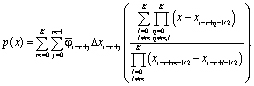
Запишем выражение для значения функции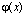
на границе ячейки:
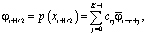
где
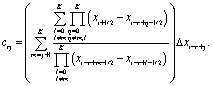
Далее полагаем что функция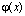
является кусочно-непрерывной. Суть ENO-аппроксимации заключается в том, что для 
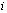-й ячейки «шаблон»
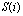нужно выбрать таким образом, чтобы избежать интерполяции через разрыв.
WENO-реконструкция основана на реконструкции ENO. Основная идея [6] заключается в том, что вместо реконструкции на одном шаблоне используется выпуклая комбинация значений полученных на каждом шаблоне.
Шаблонам
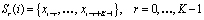
соответствует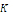 
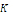значений
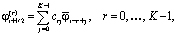
взвешенная сумма которых и принимается за значение, полученное при WENO-реконструкции:
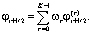
Если функция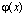
гладкая на каждом шаблоне, то найдутся коэффициенты
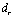такие, что
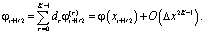
Например, для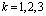
получаем:
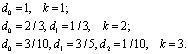
Если
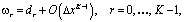
то[6]
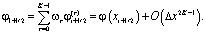
Если функция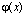
имеет разрыв на каком-то шаблоне, то соответствующий коэффициент
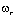должен быть близок к 0, для сохранения свойств ENO.
Предлагается рассматривать следующие весовые коэффициенты [6]:
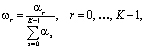
где
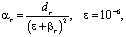
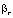– «индикатор гладкости».
Потребуем, чтобы
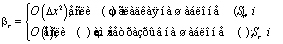
тогда
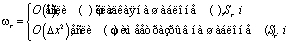
При выполнении этих условий предлагаемая аппроксимация сохраняет свойства ENO.
«Индикаторы гладкости» будем определять следующим образом:
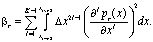
Для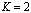
получаем:
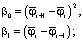
для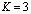
:
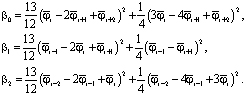
Рассмотренные алгоритмы реконструкций были реализованы в рамках пакета программ ЛОГОС. При вычислении конвективных потоков выполняется одномерная реконструкция параметров в центре грани в направлении ортогональном рассматриваемой грани. Текущая модель памяти ЛОГОС позволяет использовать шаблоны из произвольного числа ячеек. Однако организация параллельных вычислений приводит к необходимости увеличивать ширину ленты обменных ячеек. В качестве компромисса были рассмотрены схемы WENO 3-го порядка и схема WENO 3-го порядка точности с ограничителями требующие только два слоя обменных ячеек.
Разработанные алгоритмы были протестированы на ряде задач из верификационного базиса пакета программ ЛОГОС. В частности: задача о сверхзвуковом обтекании клина, задача об обтекании профиля NACA0012 при различных углах атаки, задача об обтекании профиля RAE2822 и задача об обтекании четырехзвенного профиля NASA с предкрылком и двумя закрылками.
Решалась задача о стационарном сверхзвуковом обтекании клина с числом Маха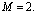
На рисунках 1-2 представлены картины распределения числа Маха в продольном сечении расчетной области для неявной и явной схем. На рисунке 3 представлена зависимость полного давления от продольной координаты вдоль сечения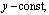 
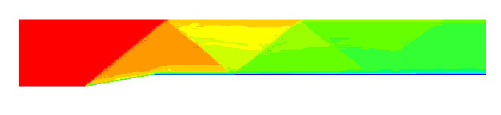
Рис. 1. – Задача о сверхзвуковом обтекании клина: распределение полного давления (неявная схема, WENO3 без ограничителей).
Рис. 2. – Задача о сверхзвуковом обтекании клина: распределение полного давления (неявная схема, WENO3 с ограничителями).
Рис. 3. – Задача о сверхзвуковом обтекании клина: распределение полного давления (явная схема,
WENO3 без ограничителей).
Рис. 4. – Задача о сверхзвуковом обтекании клина: распределение полного давления (явная схема,
WENO3 с ограничителями).
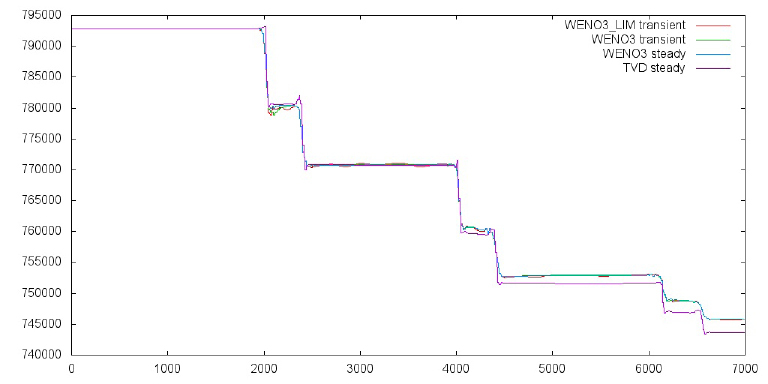
Рис. 5. – Задача о сверхзвуковом обтекании клина: зависимость полного давления от продольной координаты в сечении y=850, z=500 (WENO3_LIM transient – реконструкция WENO3 с ограничителями, нестационарное течение; WENO3 transient – реконструкция WENO3 без ограничителей, нестационарное течение; WENO3 steady– реконструкция WENO3 без ограничителей, стационарное течение; TVD steady– линейная реконструкция, используемая в методике для произвольных неструктурированных сеток, стационарное течение).
Был выполнен расчет для задачи об обтекании профиля NACA0012 потоком газа с числом Маха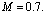 
На рисунке 4 представлена зависимость коэффициента силы сопротивления от коэффициента подъемной силы, а на рисунке 5 зависимость коэффициента подъемной силы от угла атаки. Для сравнения на рисунках 4-5 приведены экспериментальные данные [5].
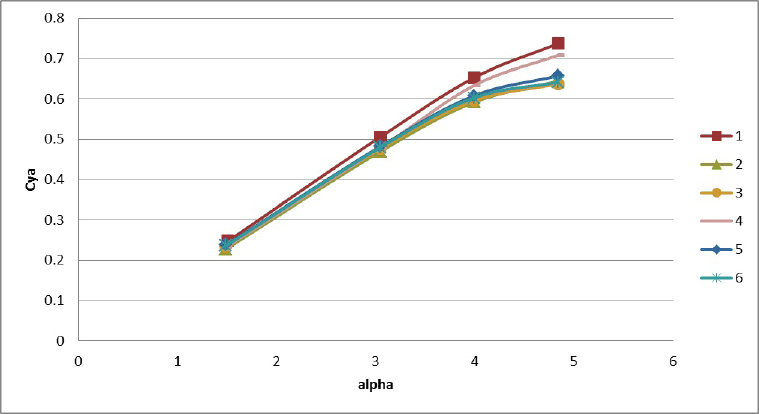
Рис. 6. – Задача об обтекании профиля NACA0012: зависимость коэффициента подъемной силы от угла атаки (1 – эксперимент; 2 – WENO-рек. без ограничителей, неявная схема; 3 – WENO-рек. с ограничителями, неявная схема; 4 – WENO-рек. с ограничителями, явная схема; 5 – WENO-рек. без ограничителей, явная схема; 6 – расчет на неструктурированной сетке модулем Logos.TVD).
Был выполнен расчет для задачи об обтекании профиля RAE2822 потоком с числом Маха 0,721 и углом атаки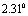 
. На рисунке 7 представлено распределение коэффициента давления на поверхности профиля.
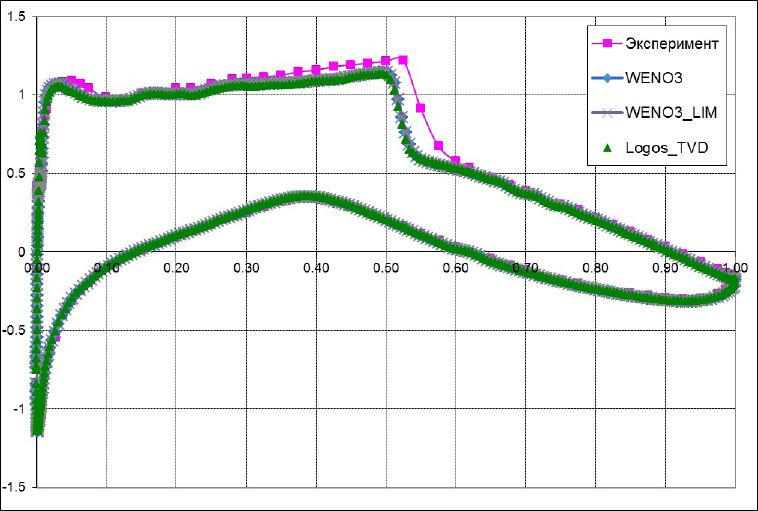
Рис. 7. – Задача об обтекании профиля RAE2822: распределение коэффициента давления по поверхности профиля (Эксперимент – экспериментальные данные [4]; WENO3 – WENO3-рек. без ограничителей; WENO3_LIM – WENO3-рек. с ограничителями; Logos_TVD – расчет на неструктурированной сетке модулем Logos.TVD).
В результате в рамках пакета программ Логос разработаны расчетные алгоритмы и создан программный модуль расчета по явным и неявным разностным схемам вязких сжимаемых течений на блочно-структурированной сетке с использованием существенно неосциллирующих схем WENO 3-го порядка точности без ограничителей и с ограничителями.
Рецензенты:
Щенников В. Н., доктор физико-математических наук, профессор, заведующий кафедрой дифференциальных уравнений факультета математики и информационных технологий ФГБОУ ВПО «Мордовский государственный университет им. Н.П. Огарёва», г. Саранск.
Малыханов Ю. Б., доктор физико-математических наук, профессор, профессор кафедры физики и методики обучения физике физико-математического факультета ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.
Библиографическая ссылка
Жалнин Р.В., Веселова Е.А., Дерюгин Ю.Н., Зеленский Д.К., Козелков А.С., Стручков А.В. ПАКЕТ ПРОГРАММ ЛОГОС. МЕТОДИКА ПОВЫШЕННОГО ПОРЯДКА ТОЧНОСТИ НА БЛОЧНО-СТРУКТУРИРОВАННЫХ СЕТКАХ С ИСПОЛЬЗОВАНИЕМ РЕКОНСТРУКЦИИ ТИПА WENO // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7329 (дата обращения: 19.04.2024).