Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Носов Г.В. 1, 1 Шишка Н.В. 1 Кулешова Е.О. 1

---

1 ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, Томский политехнический университет, Томск

В данной работе предложен расширенный метод эквивалентного генератора при постоянных и синусоидальных токах, позволяющий определить не только ток и напряжение в нагрузке, но и активную и реактивную мощности в исходной цепи, а также эффективность (КПД) передачи активной энергии от всех источников исходной цепи в нагрузку, что может быть использовано для оптимизации параметров сложных электрических цепей. Расширенный метод эквивалентного генератора дает возможность найти оптимальное сопротивление нагрузки для получения реального значения максимальной эффективности передачи в нагрузку активной энергии. Для обеспечения заданной активной мощности в исходной линейной цепи величина активной составляющей дополнительного сопротивления может принимать при определенных значениях сопротивления нагрузки отрицательные значения, что свидетельствует о том, что дополнительное сопротивление расширенного эквивалентного генератора является математическим приемом для учета реальных физических процессов в электрических цепях.

Статья в формате PDF

236 KB

реактивное сопротивление

активное сопротивление

реактивная мощность

активная мощность

ток короткого замыкания

напряжение холостого хода

активный двухполюсник

Метод эквивалентного генератора

1. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. – 11-е изд., испр. и доп. – М.: Гардарики, 2007. – 701 с.: ил.

2. Васильева О. В., Исаев Ю. Н. Применение энергетического подхода для исследования синтеза электрических цепей // Россия молодая: передовые технологии – в промышленность: Матер. II Всеросс. молодежной научно-техн. конф. – Омск, 21–22 апреля 2009. – Омск: ОмГТУ, 2009. – С. 20–23.

3. Демирчян К. С., Нейман Л. Р., Коровкин Н. В. Теоретические основы электротехники. – 5-е изд. – СПб.: Питер, 2009. – Т. 1. – 2009. – 512 с.: ил.

4. Дьяконов В. П. Mathcad 8/2000: Специальный справочник. – СПб.: Питер, 2000. – 592 с.

5. Основы теории цепей / Г. В. Зевеке [и др.]. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.

При постоянных и синусоидальных токах и напряжениях для определения в нагрузке линейной исходной цепи комплекса действующего значения тока  часто применяется метод эквивалентного генератора [1-2, 5], когда вся внешняя к нагрузке цепь как активный двухполюсник заменяется одним эквивалентным генератором с комплексом действующего значения ЭДС  и комплексным внутренним сопротивлением , где  - комплексное сопротивление нагрузки;  - комплекс действующего значения напряжения нагрузки.

В результате ток в нагрузке рассчитывается так

,                       (1)

причем ЭДС  равна напряжению холостого хода  при  и , а сопротивление  эквивалентного генератора находится с учетом тока короткого замыкания  при  и :

.                                 (2)

Однако метод эквивалентного генератора не позволяет определять суммарные с учетом нагрузки значения активной P и реактивной Q мощностей в исходной цепи, которые могут потребоваться, например, для определения оптимального значения сопротивления , обеспечивающего максимальную эффективность передачи  в нагрузку активной энергии:

,                                 (3)

где  - действующее значение тока нагрузки;  - активная мощность нагрузки.

Наряду с этим существуют методы, основанные на энергетическом подходе, когда сохраняется мощность, но не сохраняется ток [2].

Таким образом, актуальность расширения возможностей метода эквивалентного генератора с целью определения мощностей в исходной цепи не вызывает сомнений.

Описание метода

Рассмотрим вначале расширенный метод эквивалентного генератора при постоянных напряжениях и токах.

На рис. 1 представлена схема замены активного двухполюсника расширенным эквивалентным генератором с ЭДС E_Г, сопротивлением R_Г, источником тока генератора J_Г и дополнительным сопротивлением R₀. Предположим, что в исходной схеме известны для режимов:

• холостого хода (I_Н=0, R_Н=∞) напряжение в нагрузке U_H=U_ХХ и вырабатываемая мощность P_ХХ;
• короткого замыкания (U_H=0, R_Н=0) ток в нагрузке I_H=I_КЗ и вырабатываемая мощность P_КЗ.

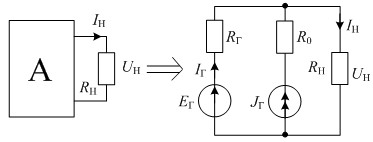
Рис. 1. Схема расширенного эквивалентного генератора

В режиме холостого хода (рис. 1) U_ХХ и P_ХХ равны:

,                            (4)

.                           (5)

Из режима короткого замыкания очевидно, что:

,                  (6)

.                   (7)

Определим параметры расширенного эквивалентного генератора ,  и R₀. При этом сопротивление генератора R_Г определяем общепринятым способом [1-2, 5]:

,                             (8)

тогда уравнения (4) и (6) объединяются. Таким образом, вместо системы из четырех уравнений необходимо решить систему из трех уравнений (4), (5) и (7).

Из уравнения (4) выразим E_Г, а из уравнения (5) выразим дополнительное сопротивление R₀:

,                                              (9)

.                                                     (10)

Подставим полученные выражения (9) и (10) в уравнение (7):

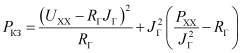.                                               (11)

Из уравнения (11) выразим ток генератора J_Г:

,                          (12)

Подставим полученное выражение в (9) и определим E_Г:

  .                                   (13)

После определения параметров генератора переходим к определению тока в нагрузке I_Н и мощности Р_Н. Записав уравнение по второму закону Кирхгофа для контура с участием тока нагрузки и используя выражение (4) или (9) с учетом (8), легко доказать, что ток в нагрузке определяется по формуле (14):

  .                                    (14)

Суммарная мощность в схеме расширенного эквивалентного генератора будет равна:

  ,                              (15)

где  (рис. 1).

Для иллюстрации работы метода рассмотрим схему, приведенную на рисунке 2, а. Преобразуем ее к схеме расширенного эквивалентного генератора (рис. 1).

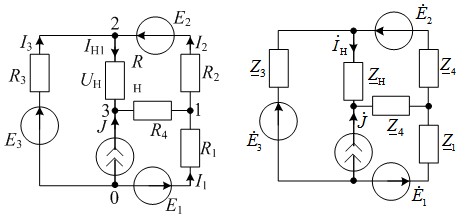
а                                                б

Рис. 2. Схема замещения цепи с параметрами: а)  E₁=150 В, E₂=200 B, E₃=150 B, J=1 A, R₁=70 Ом, R₂=20 Ом, R₃=40 Ом, R₄=10 Ом; б)  (В);  (В);  (В);  (А);  (Ом);  (Ом);  (Ом);  (Ом)

По формулам (8), (10), (12) и (13) определяем параметры расширенного эквивалентного генератора: R_Г=26,92 Ом; R₀=561,211 Ом, J_Г=-0,771 А и E_Г=169,231 В. Используя найденные параметры генератора, определяем ток в нагрузке и потребляемую мощность по формулам (14) и (15). Для сравнения определим вырабатываемую мощность P₁ и ток в нагрузке I₁=I_Н1 в исходной схеме, изменяя сопротивление нагрузки R_Н от 0 до ∞ и вырабатываемую мощность P₂ и ток в нагрузке I₂=I_Н в схеме расширенного эквивалентного генератора (рис. 3).

Ток в нагрузке, определенный в исходной схеме и методом расширенного эквивалентного генератора, совпал (рис. 4, а). Вырабатываемая мощность и КПД, определенные в исходной схеме, совпали с расчетами по методу расширенного эквивалентного генератора и не совпали с расчетами по методу эквивалентного генератора (рис. 3).

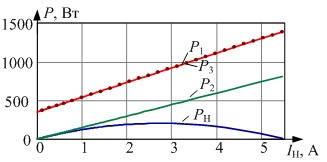
Рис. 3. Графики зависимостей мощностей от I_Н: P₁ - вырабатываемой в исходной схеме, P₂ - вырабатываемой в схеме эквивалентного генератора, P₃ - вырабатываемой в схеме расширенного эквивалентного генератора, Р_Н - мощность, потребляемая в нагрузке

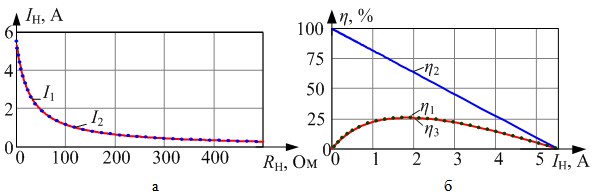
Рис. 4. Графики зависимости: а) тока в нагрузке от R_Н: I₁ - в исходной схеме, I₂ - в схеме расширенного эквивалентного генератора, б) КПД от I_Н: η₁ - в исходной схеме, η₂ - в схеме эквивалентного генератора, η₃ - в схеме расширенного эквивалентного генератора

Рассмотрим работу расширенного метода эквивалентного генератора при гармонических напряжениях и токах.

Введем в схему эквивалентного генератора (рис. 5) дополнительное комплексное сопротивление , которое совместно с сопротивлениями  и  будет задавать мощности P и Q исходной цепи (рис. 5), причем величины  и  сохраняют свои значения.

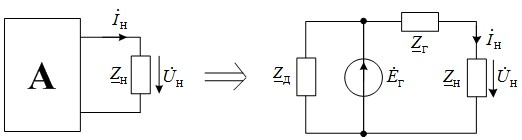
Рис. 5. Комплексная схема замещения расширенного эквивалентного генератора

В результате ток будет рассчитываться согласно (1), а сопротивление  найдем из баланса активной P и реактивной мощности Q в схеме рис. 5:

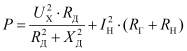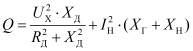 ; ,                   (16)

где  - действующее значение напряжения холостого хода.

С учетом (1) действующее значение тока нагрузки составит

   ,                                           (17)

тогда на основании формул (16) и (17) получаем расчетный параметр

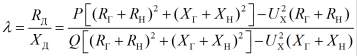   ,                            (18)

реактивную составляющую дополнительного сопротивления

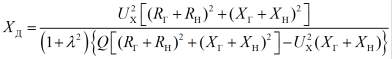,                     (19)

активную составляющую дополнительного сопротивления

   .                               (20)

В формулах (18-20) мощности P и Q являются суммарными мощностями в исходной цепи при конкретном значении сопротивления нагрузки . Очевидно, что при изменении сопротивления  будут меняться мощности P, Q и параметры дополнительного сопротивления λ, , . Поэтому из режимов холостого хода и короткого замыкания находим расчетом или экспериментально значения напряжения холостого хода  и тока короткого замыкания , по формуле (2) вычисляем сопротивление . При заданном режиме изменения нагрузки для нескольких значений сопротивления  рассчитываем или определяем экспериментально соответствующие значения мощностей P и Q, а затем вычисляем по формулам (18-20) параметры λ, R_Д, X_Д. Далее можно проводить исследования в схеме расширенного эквивалентного генератора (рис.4, б) с целью нахождения тока (1), мощностей P, Q и эффективности (3). Рассчитанные составляющие дополнительного сопротивления R_Д и X_Д могут задаваться графически или приближенными аналитическими зависимостями.

Для иллюстрации применения расширенного метода эквивалентного генератора в качестве примера рассмотрим линейную исходную цепь, комплексная схема замещения которой приведена на рис. 2, б.

Из режимов холостого хода ( ) и короткого замыкания ( ) определяем:  (В);  (В);  (А);  (Ом). Для заданных значений сопротивления нагрузки  в табл. 1 и на рис. 6 приведены полученные по формулам (1-3, 16-20) с использованием  системы Mathcad [4] результаты расчета параметров расширенного эквивалентного генератора.

Таблица 1. Параметры расширенного эквивалентного генератора

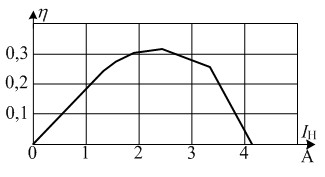
Рис. 6. Зависимость эффективности передачи в нагрузку активной энергии η от действующего значения тока нагрузки  

Точки пересечения нелинейной внешней характеристики эквивалентного генератора  с линейными зависимостями  позволяют найти действующие значения напряжения  и тока  нагрузки с фиксированным модулем сопротивления . Таким образом, для исследованной исходной цепи максимальная эффективность передачи активной энергии в нагрузку  достигается при действующем значении тока  (А). Этот ток будет при оптимальном сопротивлении нагрузки равном  (Ом), которое отличается от сопряженного значения сопротивления , т. е.  (Ом), когда наблюдается максимум активной мощности нагрузки  [2]. Следует отметить, что во многих учебниках, например, в [2], считают, что при максимуме активной мощности нагрузки эффективность (КПД) передачи активной энергии в нагрузку составляет . Это утверждение неверно для исходной сложной цепи и справедливо лишь для одноконтурной схемы, состоящей из ЭДС источника  и сопротивлений , .

Выводы

В данной работе предложен расширенный метод эквивалентного генератора при постоянных и синусоидальных токах, позволяющий определить не только ток и напряжение в нагрузке, но и активную и реактивную мощности в исходной цепи, а также эффективность (КПД) передачи активной энергии от всех источников исходной цепи в нагрузку, что может быть использовано для оптимизации параметров сложных электрических цепей.

Расширенный метод эквивалентного генератора дает возможность найти оптимальное комплексное сопротивление нагрузки для получения реального значения максимальной эффективности передачи в нагрузку активной энергии.

Для обеспечения заданной активной мощности в исходной линейной цепи величина активной составляющей дополнительного сопротивления может принимать при определенных значениях сопротивления нагрузки отрицательные значения, что свидетельствует о том, что дополнительное сопротивление расширенного эквивалентного генератора является математическим приемом для учета реальных физических процессов в электрических цепях.

Рецензенты:

Усов Юрий Петрович, д.т.н., профессор каф. ЭСиЭ ЭНИН ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск.

Федор Юрьевич Канев, д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В. Е. Зуева СО РАН, г. Томск.

Библиографическая ссылка