Предложен метод оптимальной параметрической коррекции для исследования дифференциальных уравнений и их систем с неустойчивой динамикой. Теоретической основой метода является принцип оптимальности Лагранжа. Формулируется задача оптимального управления с помощью корректирующих функций. Приводятся теоремы об условиях оптимальности. В случае существенно неустойчивой динамики на динамическую систему накладываются фазовые ограничения, а метод коррекции дополняется процедурой штрафования за их нарушение. Метод апробирован на системах Ван дер Поля, Дуффинга, Дуффинга-Холмса, Матье, Лоренца, Ресслера, связанных осцилляторах.
Пусть имеется неустойчивая по Ляпунову динамическая система, описываемая дифференциальными уравнениями:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (1.1)
, (1.1)
момент времени ![]() и числа
и числа ![]() (
(![]() ) заданы, а момент времени
) заданы, а момент времени ![]() может быть задан произвольно. Требуется перевести систему (1.1) в устойчивое состояние. Такой перевод будем называть коррекцией.
может быть задан произвольно. Требуется перевести систему (1.1) в устойчивое состояние. Такой перевод будем называть коррекцией.
Проведем коррекцию системы (1.1) вектор-функцией ![]() ,
, ![]() , компоненты которой назовём корректирующими функциями. Тогда получаем систему дифференциальных уравнений:
, компоненты которой назовём корректирующими функциями. Тогда получаем систему дифференциальных уравнений:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (1.2)
. (1.2)
Принципиально, что коррекция проводится способом ![]() или
или ![]() по доступному для этого параметру
по доступному для этого параметру ![]() . При этом разумно требовать, чтобы функции
. При этом разумно требовать, чтобы функции ![]() были оптимальными в смысле минимума затрат энергии на коррекцию:
были оптимальными в смысле минимума затрат энергии на коррекцию:
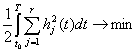 . (1.3)
. (1.3)
Пусть в системе (1.2) фазовые ограничения отсутствуют. Составим функцию Гамильтона (![]() – вектор-функция сопряжённых переменных):
– вектор-функция сопряжённых переменных):
![]() .
.
Теорема 1. Если ![]() – оптимальная корректирующая вектор-функция,
– оптимальная корректирующая вектор-функция, ![]() – соответствующая траектория, то существуют ненулевые функции
– соответствующая траектория, то существуют ненулевые функции ![]() , удовлетворяющие уравнениям
, удовлетворяющие уравнениям
![]() ,
, ![]() ,
, ![]() ,
,
и выполняются условия стационарности:
![]() ,
, ![]() .
.
При наличии фазовых ограничений вида ![]() ,
, ![]() , их учёт может производиться методом штрафных функций. А именно, составляется штрафная функция:
, их учёт может производиться методом штрафных функций. А именно, составляется штрафная функция:
![]() ,
,
где ![]() – коэффициент штрафа, которая добавляется в гамильтониан:
– коэффициент штрафа, которая добавляется в гамильтониан:
![]()
Введем функционал:
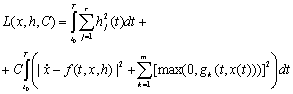
Теорема 2. Для любого ![]() решение задачи:
решение задачи:
![]()
существует, и имеют место равенства:
![]()
Теорема 3. Если ![]() – оптимальная корректирующая вектор-функция,
– оптимальная корректирующая вектор-функция, ![]() – соответствующая траектория, то существуют ненулевые функции
– соответствующая траектория, то существуют ненулевые функции ![]() и значение параметра штрафа
и значение параметра штрафа ![]() , что:
, что:
![]() ,
, ![]() ,
, ![]() ,
,
и выполняются условия стационарности:
![]() ,
, ![]() .
.
Теорема 3 расширяет алгоритм метода оптимальной параметрической коррекции. Оптимальная траектория ![]() находится интегрированием следующих уравнений и подбором
находится интегрированием следующих уравнений и подбором ![]() :
:
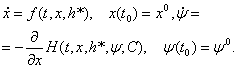
К задаче (1.2)-(1.3) применима теорема IV (см.: Малкин И.Г. Теория устойчивости движения. М.: Наука 1966, стр. 485), адаптированную формулировку которой мы приводим ниже. Введем функцию (![]() – функция Ляпунова):
– функция Ляпунова):
![]() .
.
Теорема 4. Если для дифференциальных уравнений возмущенного движения (1.2) можно найти допускающую бесконечно малый низший предел определенно-положительную функцию ![]() и вектор-функцию
и вектор-функцию ![]() ,
, ![]() , удовлетворяющие в области
, удовлетворяющие в области ![]() условиям: 1) справедливо равенство
условиям: 1) справедливо равенство ![]() ; 2) какова бы ни была функция
; 2) какова бы ни была функция ![]() , справедливо неравенство
, справедливо неравенство ![]() , то функция
, то функция ![]() разрешает задачу об оптимальной устойчивости системы (1.1). При этом выполняются равенства
разрешает задачу об оптимальной устойчивости системы (1.1). При этом выполняются равенства
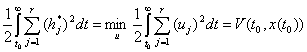 .
.
Работа выполнена при финансовой поддержке Минобразования РФ.
Библиографическая ссылка
Тараканов А.Ф., Талагаев Ю.В. МЕТОД ОПТИМАЛЬНОЙ ПАРАМЕТРИЧЕСКОЙ КОРРЕКЦИИ ДЛЯ ОБЕСПЕЧЕНИЯ УСТОЙЧИВОСТИ ДИНАМИЧЕСКИХ СИСТЕМ // Современные проблемы науки и образования. 2006. № 3. ;URL: https://science-education.ru/ru/article/view?id=341 (дата обращения: 05.03.2026).



