По данным статистики ЕГЭ по математике (профиль) только 4,2% абитуриентов решают правильно задачи с параметрами (задание № 18), эти задания относятся к уровню сложности «высокий» и оцениваются максимально 4 баллами [1]; из бесед следует, что большинство абитуриентов не знакомы с методами решения таких задач. Без качественной школьной подготовки невозможно сформировать у подрастающего поколения фундаментальные знания, что является необходимым условием для успешного изучения в технических вузах высшей математики и других базовых дисциплин.
Проблемой обучения школьников решению задач с параметрами занимались М.И. Башмаков, Ю.М. Важенин, В.А. Далингер, А.Г. Мордкович, Г.И. Саранцев и др.
Практика проведения вступительных экзаменов, ЕГЭ и олимпиад по математике показывает, что задачи с параметрами являются для старшеклассников задачами повышенной сложности, при решении которых необходимо не только знание разнообразных методов и приемов, но и гибкость математического мышления. В школьной программе по математике мало времени уделяется решению такого рода задач, и многим абитуриентам они не по силам.
Цель исследования: формирование у абитуриентов фундаментальных знаний по математике посредством изучения нестандартных методов при решении задач с параметрами из повышенного уровня ЕГЭ (профиль).
Материал и методы исследования. В исследовании принимали участие абитуриенты, обучающиеся на подготовительных курсах, ученики школ 10–11-х классов, учителя-предметники, эксперты ЕГЭ. Был проведен анализ литературы, в которой описывались различные методы решения задач с параметрами [2–4].
Разумная классификация задач с параметрами по методам решений достаточно затруднительна, поскольку каждая из них является в определенной степени нестандартной и творческой. Наиболее часто используемые методы решения задач с параметрами: графический метод, метод оценки, метод симметрии, использование ограниченности и монотонности функций и т.п.
Одним из наиболее эффективных методов решения задач с параметрами служит графический способ. Он является более доступным и понятным для старшеклассников в связи со своей наглядностью. Мы остановимся на других методах решения нестандартных задач, в которых требуются логические суждения и умение анализировать различные ситуации. Решение таких задач вызывает у школьников затруднения как в логическом, так и в техническом плане.
Задача 1. Найдите все значения 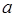 , при каждом из которых уравнение
, при каждом из которых уравнение
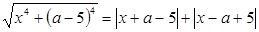 имеет единственное решение.
имеет единственное решение.
Решение. В первую очередь замечаем, что можно ввести замену по параметру: 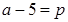 . В силу этого уравнение примет симметрический вид:
. В силу этого уравнение примет симметрический вид:
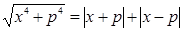 (1).
(1).
Введем функцию 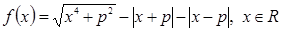 . Уравнение (1) примет вид:
. Уравнение (1) примет вид: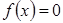 . Легко проверить, что
. Легко проверить, что 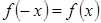 , т.е. функция четная. Следовательно, если
, т.е. функция четная. Следовательно, если 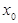 является корнем уравнения, то и
является корнем уравнения, то и 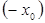 также корень данного уравнения. По условию решение должно быть единственным, т.е. может быть только
также корень данного уравнения. По условию решение должно быть единственным, т.е. может быть только 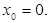 Подставим его в уравнение (1):
Подставим его в уравнение (1): 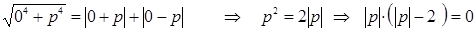 .
.
Корни этого уравнения 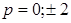 . При этих значениях
. При этих значениях 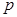 мы гарантируем, что ноль является корнем, но утверждать, что он единственный, не можем. Поэтому надо подставить найденные значения параметра в уравнение (1) и проверить количество решений при каждом из них.
мы гарантируем, что ноль является корнем, но утверждать, что он единственный, не можем. Поэтому надо подставить найденные значения параметра в уравнение (1) и проверить количество решений при каждом из них.
Если 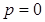 , то
, то 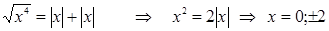 .
.
Получили три решения, следовательно, 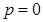 не подходит.
не подходит.
Если 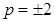 , то
, то 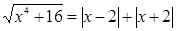 .
.
Поскольку обе части неотрицательны, то возведем в квадрат: 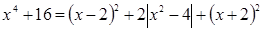 ,
,
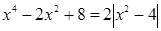 . (2)
. (2)
Решим уравнение (2), раскрыв модуль по определению:
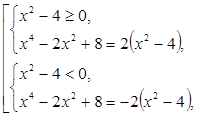
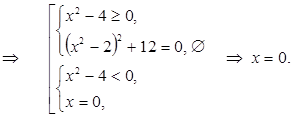
Получили единственное решение, следовательно, 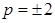 подходит. Тогда находим соответствующие значения параметра
подходит. Тогда находим соответствующие значения параметра 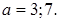
Ответ: 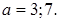
Отметим важные шаги решения. Во-первых, при решении данной задачи нужно было обратить внимание на единственность решения (в общем случае – нечетность количества корней) и четность уравнения относительно неизвестной. Во-вторых, правильно сделать вывод, что нам дает нахождение значений параметра 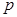 , если ноль является корнем уравнения. Решения уравнения (2) было найдено аналитическим способом. Можно было показать количество решений и графическим способом.
, если ноль является корнем уравнения. Решения уравнения (2) было найдено аналитическим способом. Можно было показать количество решений и графическим способом.
Задача 2. Найдите значения 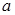 , при каждом из которых решение уравнения
, при каждом из которых решение уравнения
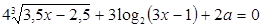 принадлежит отрезку
принадлежит отрезку 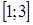 .
.
Решение. Введем функцию 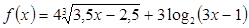 , определенную на интервале
, определенную на интервале 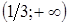 . Данная функция является непрерывно возрастающей в своей области определения как сумма двух непрерывно возрастающих функций.
. Данная функция является непрерывно возрастающей в своей области определения как сумма двух непрерывно возрастающих функций.
Поэтому множеством значений функции 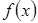 на отрезке
на отрезке 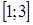 будет являться промежуток
будет являться промежуток 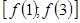 . Вычислим значения функции в граничных точках отрезка:
. Вычислим значения функции в граничных точках отрезка:
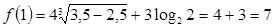 ;
; 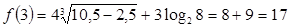 .
.
Получаем, что множество значений функции на данном промежутке 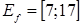 .
.
Исходное уравнение можно записать в виде 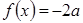 , и по условию оно должно иметь решения на промежутке
, и по условию оно должно иметь решения на промежутке 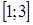 . Это равносильно, что значение
. Это равносильно, что значение 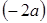 попадает в множество значений функции
попадает в множество значений функции 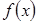 на данном отрезке, т.е.
на данном отрезке, т.е. 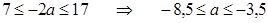 .
.
Ответ: 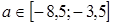 .
.
Первое впечатление от этого задания – это «нереальность» его решения в общем случае, поэтому надо использовать один из методов нестандартного решения: графический метод, оценка, монотонность функции и т.п. Конкретно к этому типу задания однозначно применяется метод монотонности функции.
В следующем примере также используется этот же метод, но в техническом плане решение будет другим.
Задача 3. Найдите значения 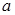 , при каждом из которых уравнение
, при каждом из которых уравнение
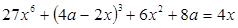 не имеет корней.
не имеет корней.
Решение. Преобразуем уравнение: 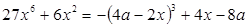 или
или
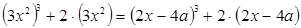 . (3)
. (3)
Пусть 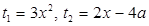 , тогда уравнение (3) примет вид:
, тогда уравнение (3) примет вид: 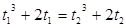 .
.
Введем вспомогательную функцию: 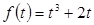 . Отметим, что данная функция является возрастающей при
. Отметим, что данная функция является возрастающей при 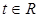 , т.к.
, т.к. 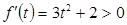 .
.
В силу монотонности функции 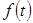 имеем
имеем 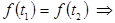
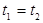 .
.
Значит, 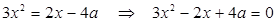
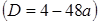 .
.
По условию уравнение не имеет корней, т.е. дискриминант 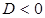 :
:
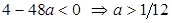 .
.
Ответ: 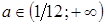 .
.
Задача 4. Найдите значения 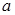 , при каждом из которых уравнение
, при каждом из которых уравнение
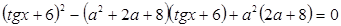
имеет на отрезке 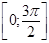 ровно два решения.
ровно два решения.
Решение. Отметим, что 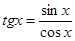 существует, если
существует, если 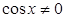 , т.е.
, т.е. 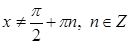 . С учетом нашего промежутка получаем
. С учетом нашего промежутка получаем 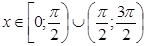 .
.
Введем замену 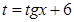 . Получим уравнение:
. Получим уравнение:
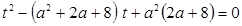 .
.
По обратной теореме Виета имеем:
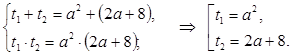
Функция 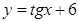 является возрастающей на своей области определения, поэтому если 1)
является возрастающей на своей области определения, поэтому если 1) 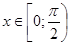 , то
, то 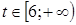 ; 2) если
; 2) если 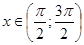 , то
, то 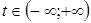 .
.
Таким образом, если 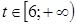 , то получим два решения по переменной
, то получим два решения по переменной 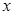 ; если
; если 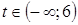 , то получим одно решение по переменной
, то получим одно решение по переменной 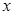 .
.
Для выполнения условия задачи возможны два случая:
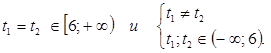
1. 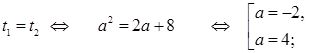
Получаем, что если 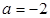 , то
, то 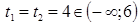 , т.е. уравнение имеет одно решение, что не удовлетворяет условию задачи.
, т.е. уравнение имеет одно решение, что не удовлетворяет условию задачи.
Если 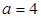 , то
, то 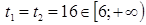 , т.е. уравнение имеет два решение. Следовательно, значения
, т.е. уравнение имеет два решение. Следовательно, значения 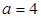 подходит.
подходит.
2. Если 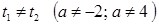 , то
, то
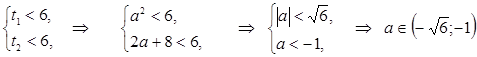 .
.
Таким образом, 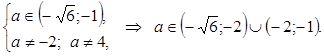
Ответ: 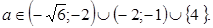
Замечания по задаче:
1) при решении этой задачи сразу «напрашивались» замена переменной и сведение исходного уравнения к квадратному;
2) нахождение корней по обратной теореме Виета не обязательно, можно было вычислить дискриминант, который получился бы полным квадратом;
3) после введения переменой необходимо прописать множество значений новой величины;
4) требуется проанализировать ситуации получения нужного количества корней уравнения.
Следующая задача по структуре очень похожа: замена переменной и сведение к исследованию корней квадратного уравнения, но проверка ограничений (ОДЗ) будет более тщательной.
Задача 5. Найдите значения 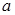 , при каждом из которых уравнение
, при каждом из которых уравнение
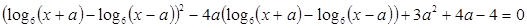
имеет ровно два решения.
Решение. Выпишем ОДЗ: 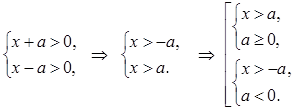
Введем замену 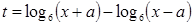 .
.
Получим уравнение: 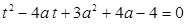 . (4)
. (4)
Вычислим дискриминант
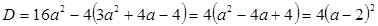 .
.
Если 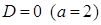 , то
, то 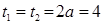 .
.
Если 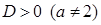 , то
, то 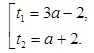
Пусть 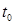 – корень уравнения (4). Найдем соответствующее значение неизвестной
– корень уравнения (4). Найдем соответствующее значение неизвестной 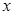 .
.
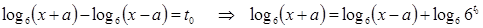 ,
,
 ,
,
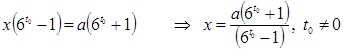 .
.
Если 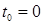 , то
, то 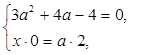 система не имеет решения.
система не имеет решения.
Вычислим значения 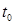 , при которых
, при которых 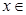 ОДЗ.
ОДЗ.
1. Если 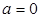 , то
, то 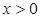 :
: 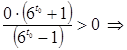 не имеет решения.
не имеет решения.
2. Если 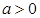 , то
, то 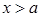 :
:
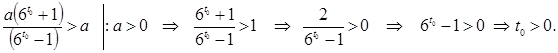
3. Если 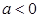 , то
, то 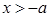 :
:
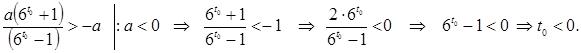
Таким образом, ОДЗ по переменной 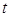 :
: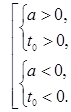 (5)
(5)
По условию нам нужно ровно два решения по переменной 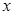 , тогда и по переменной
, тогда и по переменной 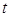 тоже должно быть два различных решения, удовлетворяющих ОДЗ (5).
тоже должно быть два различных решения, удовлетворяющих ОДЗ (5).
Выше получили, что при 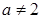 :
: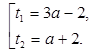
1. 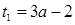 :
: 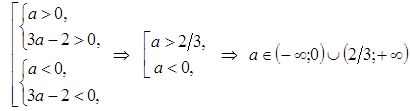 .
.
2. 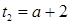 :
: 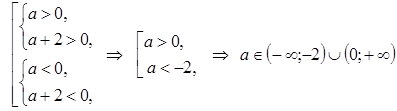 .
.
Получаем 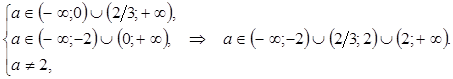
Ответ: 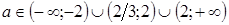 .
.
Отличие трех решений заключается в различных способах проверки ограничений.
Для создания математической модели данной задачи требуются гибкость мышления и уверенное владение математическим аппаратом.
Результаты исследования и их обсуждение. Абитуриенты и школьники обучились новым приемам и методам решения сложных нестандартных задач с параметрами. Полученные навыки являются мощным инструментом формирования фундаментальных знаний, а также повышают уровень развития математической культуры.
Выводы. Абитуриенты, способные решать задачи с параметрами, более успешно справляются и с другими заданиями ЕГЭ, умеют конструировать новые способы решения задач, осознанно выбирают рациональные методы решения, решают задачи несколькими способами, более того – увеличиваются скорость и качество техники решения задач.
Заключение. Задачи с параметрами относятся к заданиям повышенного уровня и располагаются в вариантах профильного ЕГЭ по математике на последних позициях. Оцениваются они более высокими первичными баллами и предназначены для тех абитуриентов, которые претендуют на высокий экзаменационный балл. Изучение нестандартных методов на примере решения задач с параметрами [5–7] не только позволяет расширить область успешно решаемых задач по математике, но и способствует развитию у старшеклассников нестандартного, конструктивного математического мышления, которое необходимо для будущих инженеров.
Библиографическая ссылка
Матвеева Т.А., Светличная В.Б., Мустафина Д.А., Ребро И.В., Рахманкулова Г.А. ОСОБЕННОСТИ МЕТОДОВ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ ПО МАТЕМАТИКЕ С ПАРАМЕТРАМИ // Современные проблемы науки и образования. 2020. № 2. ;URL: https://science-education.ru/ru/article/view?id=29667 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/spno.29667



