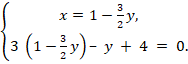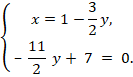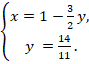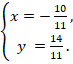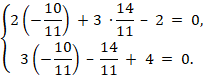Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Стефанова Г.П. 1 Байгушева И.А. 1 Товарниченко Л.В. 1 Степкина М.А. 1

---

1 ФГБОУ ВО "Астраханский государственный университет"

Статья представляет собой теоретический анализ проблемы формирования познавательной само-стоятельности студентов современного вуза, обзор степени разработанности проблемы в психолого-педагогической литературе. Познавательная самостоятельность студента рассматривается авторами как необходимое условие его профессионального становления и ключевая компетентность выпускника вуза, что обусловлено потребностью рынка труда в конкурентоспособных специалистах, способных к профес-сиональной мобильности, непрерывно повышающих уровень своей компетентности в избранной области профессиональной деятельности. Авторами с позиций деятельностного подхода уточнено содержание понятие «познавательная самостоятельность студента». В статье обоснована целесообразность формирования познавательной самостоятельности первокурсников в рамках учебного курса «Практикум по элементарной математике». На основе разработанной авторами обобщенной схемы решения математических задач данного учебного курса выделены формируемые при её реализации виды познавательной деятельности студента. В качестве необходимого педагогического условия формирования познавательной активности и самостоятельности студентов рассмотрено использование активных и интерактивных методы обучения. Представлен опыт профессорско-преподавательского состава Астраханского государственного университета по разработке и внедрению таких методов (визуализация аналитических формул, создание командных квест-формул, «обратный отсчет», «хочу все знать») при реализации учебного курса «Практикум по элементарной математике».

Статья в формате PDF

535 KB

познавательная самостоятельность студентов

виды познавательной деятельности

активные и интерактивные методы обучения

1. Хрестоматия по истории педагогики: в 3 т. / под. ред. А.И. Пискунова. - М.: Сфера. 2009. - 512 с.

2. Гурина И.А., Шпак О.В. Проблема развития познавательной самостоятельности как качества личности в отечественной психологии // Современные проблемы науки и образования. - 2014. - № 5. - С. 644.

3. Лежнева Н.В. Познавательная самостоятельность студентов вуза при переходе к ФГОС ВПО: постановка проблемы // Новое в психолого-педагогических исследованиях. – 2013. - № 4. – С. 108-114.

4. Новикова И.Ю. Познавательная самостоятельность как качество личности // Наука. Образование. Личность. - 2014. – Т. 2. – С. 66-70.

5. Пустовойтов В.Н. Трансформация содержания категорий «познавательная активность», «познавательная самостоятельность» и «познавательная компетентность» в современных отечественных научных исследованиях // Научное обозрение. Педагогические науки. – 2017. - № 2. – С. 88-92.

6. Носикова Я.Н., Обухов А.С. Социально-педагогическая обусловленность развития познавательной самостоятельности младших школьников в процессе учебно-исследовательской деятельности // Проблемы современного образования. - 2018. № 1. - С. 111-120.

7. Товарниченко Л.В., Степкина М.А. Актуализация математических знаний первокурсников // Наука и школа. – 2016. - № 5. С. 102-106.

8. Степкина М.А., Байгушева И.А. О готовности первокурсников к изучению математики в вузе // Преподаватель XXI век. – 2016. - № 4. – С. 211-219.

9. Стефанова Г.П., Крутова И.А., Байгушева И.А. Типовые профессиональные задачи как целевой ориентир подготовки бакалавров и магистров в условиях реализации ФГОС ВО // Известия Волгоградского государственного педагогического университета. – 2017. – № 3 (116). – С. 53-58.

10. Привалова Г.Ф. Активные и интерактивные методы обучения как фактор совершенствования учебно-познавательного процесса в вузе // Современные проблемы науки и образования. – 2014. – № 3. - URL: http://www.science-education.ru/ru/article/view?id=13161 (дата обращения: 25.07.2018).

Государственная политика развития высшего образования определяет необходимость подготовки специалистов, готовых и способных компетентно решать профессиональные задачи в соответствии с направлением и уровнем подготовки в условиях неопределенности динамично развивающегося общества. Актуальность целенаправленного формирования познавательной самостоятельности студентов в качестве основы их успешного профессионального становления обусловлена следующими факторами:

· ускорение темпов социально-экономического развития и обновления знаний объективно требует от специалистов умения учиться всю жизнь, самосовершенствоваться в области профессиональной деятельности;

· самостоятельная работа как форма учебной деятельности согласно требованиям ФГОС ВО (3+) является важным элементом образовательного процесса: общий объем часов самостоятельной работы студентов очной формы обучения (бакалавриат) составляет 50-70% трудоёмкости учебных дисциплин;

· доля студентов с достаточно высоким начальным уровнем познавательной самостоятельности не превышает 15-20%.

Как справедливо отметил выдающийся немецкий педагог А. Дистервег, «развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий… должен достигнуть этого собственной деятельностью... То, чего человек не приобрел путем своей самостоятельности – не его» [1]. Познавательная самостоятельность студента имеет чрезвычайно важное значение для его профессионального становления в высшей школе. Действительно, ведь в процессе своей будущей профессиональной деятельности специалист должен будет самостоятельно решать профессиональные задачи, что подразумевает их постановку, диагностирование типа задачи, планирование и реализацию деятельности по решению задач. В процессе самостоятельной учебной деятельности студент «учится учиться», используя полученные знания для решения новых задач. А это умение необходимо специалисту при современных темпах социально-экономического и научно-технического развития, чтобы поддерживать высокий уровень своей профессиональной компетентности. И, наконец, развитие интеллектуального и творческого потенциала личности невозможно без систематического самостоятельного поиска (выбора) методов решения задач. Согласимся с И.А. Гуриной и О.В. Шпак: «самостоятельность в обучении интегрирует в себе интеллект, способности, характер и чувства, которые, в свою очередь, развиваются в самостоятельной деятельности и формируют способность добиваться поставленных задач» [2]. Таким образом, сформированная познавательная самостоятельность является ключевой профессиональной компетенцией выпускника вуза, лежит в основе его способности к инновационной деятельности и прогнозированию её результатов.

Целью предпринятого авторами исследования является уточнение содержания понятия «познавательная самостоятельность студента» с позиций деятельностного подхода и разработка методических аспектов формирования видов познавательной самостоятельной деятельности студентов на основе обобщенной схемы решения математических задач в рамках специального учебного курса «Практикум по элементарной математике».

Материал и методы исследования. В психолого-педагогической литературе предложены различные трактовки понятия «познавательная самостоятельность»:

· качество личности, характеризующееся готовностью обучаемого своими силами осуществлять познавательную деятельность для решения новой познавательной проблемы [3];

· интегративное качество личности, вызванное стабильным интересом к познавательной деятельности, познавательной активности и реализующееся в познавательном поиске, проявляющемся в потребности постоянного приумножения и углубления ранее освоенных знаний, умений и навыков с целью преобразования окружающей действительности [4];

· метакомпетентность личности, активизирующая и стимулирующая развитие других её компетентностей во многих сферах деятельности [5];

· интегративное качество личности, которое выражается в единстве интеллектуальных, мотивационных, эмоционально-волевых характеристик, проявляющихся в стремлении к самообразованию, поиску новых знаний и способности оперировать ими на практике; в умении сознательно ставить перед собой цели и задачи, обеспечивая их качественное выполнение; в признании самостоятельного познания высшей формой творческой мыслительной деятельности [6];

· свойство личности, которое проявляется в желании своими силами овладеть знаниями и способами деятельности [7] и др.

Анализ общего содержания существующих дефиниций привел к заключению, что познавательная самостоятельность студента может рассматриваться только через познавательную деятельность, а именно как способность и готовность ставить и достигать без посторонней помощи цели познавательных видов деятельности, направленных на освоение теоретико-практических основ специальности. Познавательная деятельность студентов имеет, на наш взгляд, следующие отличия от познавательной деятельности школьников:

· мотивация и личностные качества студентов оказывают большее влияние на их познавательную деятельность, чем у школьников;

· познавательная деятельность студентов имеет профессиональную направленность;

· познавательная деятельность студентов опирается на систему приобретенных базовых знаний и умений;

· преподаватель, выступая организатором познавательной деятельности студентов, в меньшей степени контролирует выполнений всех её действий по сравнению со школьным учителем, большее значение приобретают самоконтроль и взаимный контроль студентов.

Принимая во внимание важную роль математики в системе высшего образования специалистов технических, экономических и естественно-научных направлений подготовки, а также неудовлетворительный уровень готовности абитуриентов к изучению математики в вузе [8], считаем целесообразным формировать познавательную самостоятельность у студентов-первокурсников в процессе специально организованного учебного курса «Практикум по элементарной математике». Изучение такого курса преследует двоякую цель: 1) актуализировать математические знания, необходимые для изучения математических дисциплин в вузе; 2) cформировать познавательную самостоятельность, используя «знакомый» студентам материал школьного курса математики.

В рамках психологической теории деятельности выделены три класса видов познавательной деятельности: общие (умения определять цель деятельности, планировать и контролировать деятельность и др.), логические (сравнение, подведение под понятие, выведение следствий, классификация и др.) и специфические, используемые в конкретной области знаний. Для математики специфическими видами познавательной деятельности являются построение и преобразования графиков функций, тождественные преобразования алгебраических выражений, построение математической модели задачи и др.

Основным средством формирования всех видов познавательной деятельности в курсе «Практикума по элементарной математике» являются математические задачи школьного курса математики. На основе алгоритма выделения обобщенных методов решения типовых задач [9] разработана обобщенная схема решения математических задач, выделены формируемые при её реализации виды познавательной деятельности (табл. 1). Проиллюстрируем на примере решения конкретной задачи: найти точку пересечения двух прямых на плоскости 2x + 3y – 2 = 0, 3x – y + 4 = 0.

Таблица 1

Обобщенная схема решения математических задач

Формирование видов познавательной деятельности происходит в результате их многократного применения при реализации обобщенной схемы решения математических задач в различных конкретных ситуациях.

Результаты исследования. Чтобы познавательная самостоятельность стала качеством личности студента, у него должны быть сформированы не только виды познавательной деятельности, но и способность индивидуально и в коллективе других студентов осуществлять такую деятельность без помощи преподавателя. Тогда студент из субъекта познавательной деятельности превращается в её активного участника, организатора, несет ответственность за её результаты.

Как показывает опыт, важную роль в процессе формирования познавательной самостоятельности студентов играют активные и интерактивные методы обучения, широкое использование которых является одним из требований ФГОС ВО к организации учебного процесса. А. Дистервег оценивал эффективность метода обучения на основании того, насколько он мобилизует умственные силы учащихся: «Всякий метод плох, если приучает учащегося к простой восприимчивости или пассивности, и хорош, если возбуждает в нем самодеятельность» [1]. Эффективность применения активных и интерактивных методов для формирования познавательной самостоятельности студентов достигается благодаря тому, что студенты:

· самостоятельно находят пути решения поставленной учебной задачи;

· получают возможность для совместной командной работы, которая развивает толерантность, лидерство, ответственность;

· могут сформировать собственную точку зрения, опирающуюся на определенные факты, и аргументированно её отстаивать;

· выходят на уровень осознанной профессиональной компетентности [10].

Кратко остановимся на некоторых интерактивных методах обучения, применяемых в процессе изучения курса «Практикум по элементарной математике».

Одним из таких методов является метод визуализации аналитических формул и создания командных квест-формул. Эту технологию удобно использовать в процессе изучения любых функций. При этом занятие конструируется таким образом, чтобы каждый студент был задействован в учебном процессе и результат его деятельности являлся не только его индивидуальным достижением, но частью коллективной деятельности команды студентов. Группу студентов делят на команды по 5-6 человек. Деление может происходить как намеренным образом, когда преподаватель заранее формирует команды, так и случайным образом. Заметим, что способ случайного разбиения оказывает более эффективное педагогическое воздействие на студентов, поскольку благодаря опыту совместной познавательной деятельности с разными членами группы у студентов формируются такие качества, как толерантность, стрессоустойчивость, умение работать в команде, развиваются лидерские качества. Развитие этих качеств поможет будущим специалистам подготовиться к успешному выполнению будущей профессиональной деятельности в условиях реального производства.

Каждый член команды получает индивидуальную квест-формулу, задающую функцию. Он должен её графически визуализировать и по полученному графику найти отдельные числовые параметры функции. Затем, с использованием полученных членами команды числовых параметров, по заданному алгоритму команда формирует общую квест-формулу, с помощью которой выполняется общекомандное задание. При такой форме проведения занятия студенты, как было замечено выше, активно включаются во взаимодействие и сотрудничество с другими участниками учебного процесса в соответствии с принципом «равные обучают равных», так как для достижения общекомандного результата члены команды помогают друг другу, обсуждая и совместно преодолевая возникающие трудности.

Приведем пример ещё одного метода обучения, названного нами «Обратный отсчёт» (табл. 2). Метод можно использовать при изучении тем, связанных с преобразованием выражений (рациональных, иррациональных, логарифмических, тригонометрических и др.). Каждый член команды получает пакет с индивидуальным заданием, состоящим в преобразовании алгебраического выражения (упростить, представить в заданном виде и т.п.).

Таблица 2

Пример заданий членов одной команды для метода «Обратный отсчет»

Из преобразованных членами команды выражений составляется по заданному алгоритму новое выражение (табл. 3). Команде необходимо преобразовать это выражение, и в результате получается значение выражения. Затем каждый член команды находит значение своего выражения от полученного общекомандного значения.

Таблица 3

Пример общекомандной задачи

Метод «Хочу всё знать» помогает студентам глубоко вникать в содержание математических понятий и может использоваться в качестве пропедевтики их изучения. Так, например, перед изучением темы «Предел функции» в курсе математического анализа со студентами можно провести подготовительное занятие в рамках дисциплины «Практикум по элементарной математике». Группу студентов делят на команды по 3-5 человек в каждой. Одна команда – это корпорация. Каждый участник команды – это фирма данной корпорации. Участники команды получают индивидуальные задания, в которых им надо найти предельные значения своей производственной функции при бесконечном увеличении спроса на продукцию. Находя предельное значение, студенты вникают в содержание понятия предела, ещё не зная самого понятия. Приведём пример таких заданий (табл. 4).

Таблица 4

Пример заданий членов одной команды для метода «Хочу всё знать»

Затем все члены команды находят совместную прибыль своей корпорации при заданных издержках и ценах на единицу продукции (табл. 5).

Таблица 5

Пример общекомандной задачи

Заключение. В процессе такого занятия осуществляется пропедевтика новых понятий, формируются навыки математической деятельности и профессиональные компетенции будущих специалистов. Профессорско-преподавательским составом Астраханского государственного университета разработано необходимое учебно-методическое обеспечение курса «Практикум по элементарной математике» (учебное пособие, рабочая тетрадь, программа-конструктор учебных задач, тесты) и накоплен значительный опыт применения интерактивных методов обучения.

Опыт внедрения результатов исследования позволяет утверждать, что в процессе реализации учебного курса «Практикум по элементарной математике», в рамках которого использовались интерактивные методы обучения с использованием обобщенной схемы решения математических задач, у студентов-первокурсников успешно формируются готовность и способность своими силами продвигаться в овладении математическими знаниями, пропадает неуверенность в своих силах при изучении математических дисциплин в вузе.

Библиографическая ссылка