Анализ рассмотренных процессов актуален для совершенствования электроразрядных технологий и диктуется требованиями оптимизации параметров генератора и режимов разряда, согласованных с волновой динамикой в обрабатываемом материале и условиями его разрушения.
Для решения этой проблемы предложена физико-математическая модель, согласованно описывающая разряд конденсатора и динамику электровзрыва, связь электротехнических характеристик с напряженно-деформированным состоянием материала, вызывающим его разрушение.
Физико-математическая модель электровзрыва

Электротехническая часть электровзрыва описывается разрядом конденсатора С в цепи (рис.1).
Рис. 1. Электрическая схема разрядной цепи
При замыкании ключа S (рис. 1) в диэлектрике формируется разрядный канал радиусом rch0, в плазме которого и в активном сопротивлении rz (сопротивление коммутатора S и проводов разрядного контура) из конденсатора С выделяется запасенная в нем энергия Wg = CU02/2. Индуктивность L состоит из индуктивности конденсатора С, соединительных проводов и разрядного канала длиной lch. Канал разряда с сопротивлением Rch(t) моделировался цилиндром радиусом rch(t) и длиной lch, расширяющимся в радиальном направлении (рис. 2).
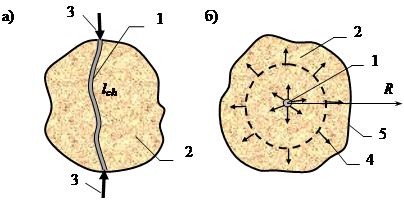
Ввод энергии в плазменный канал приводит к росту давления в нем, увеличению его радиальных размеров, генерированию волн механических напряжений. Необходимо отметить, что быстрозатухающие ударные волны в конденсированных диэлектриках с давлением на фронте до 108–109 Па наблюдаются уже на стадии формирования ветвящихся разрядных каналов. Однако основное разрушающее действие оказывают волны давления, генерируемые при радиальном расширении канала после завершения пробоя.
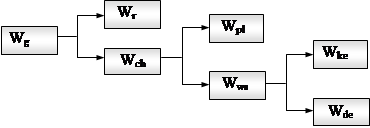
Без учета энергетических потерь на электрический пробой (обычно составляющих порядка 10 Дж) схема преобразования энергии приведена на рисунке 3. Энергия накопителя Wg при разряде конденсатора частично расходуется в активном сопротивлении контура Wr и в основном выделяется в разрядном канале Wch. Последняя составляющая расходуется на нагрев плазмы Wpl и совершение работы по ее расширению Wws, т.е. в энергию ударной волны в твердом теле. Среда, охваченная волной, деформируется в радиальном направлении и расширяется. Энергия волны трансформируется во внутреннюю энергию твердого тела Wde и кинетическую энергию его центробежного движения относительно канала Wke.
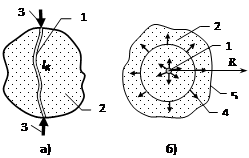
Рис. 3. Схема преобразования электрической энергии в энергию ударно-волнового возмущения
Потерями энергии на формирование канала пробоя пренебрегаем. Потери энергии, вызванные излучением и возможным истечением продуктов разряда из канала, в расчетах не учитывались. Нагружаемый материал в рассматриваемом интервале времени полагался сплошным. Прогноз разрушающего действия электровзрыва проводился на основе эпюр тангенциального напряжения и радиального распределения энергии в волне. При этом полагалось, что разрушающее действие обусловлено только энергией деформирования среды.
Согласно схеме преобразования энергии и с учетом принятых допущений математическая модель включала: уравнения Кирхгофа разрядной цепи, уравнение энергобаланса разрядного канала и уравнения, описывающие упругопластическое деформирование твердой среды вокруг канала.
Уравнения Кирхгофа
![]() (1)
(1)
с начальными условиями для силы тока i(0)=0 и напряжения U(0)=U0, где U0 – начальное напряжение, позволяют рассчитать силу тока в цепи i(t), сопротивление канала Rch(t), омические потери в цепи WR на rz и динамику энерговвода в плазму канала Wch(t):
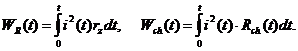 (2)
(2)
Сопротивление плазменного канала определялось через интеграл действия тока по соотношению Ромпе—Вайцеля, широко применяемому для искры в газах:
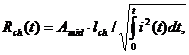 (3)
(3)
где Аmid=611 В·с1/2м-1 – искровая постоянная [2].
Зависимости Wch(t) использовались в уравнении энергобаланса канала, которое является ключевым соотношением, связывающим электротехническую часть электровзрыва с волновой динамикой в среде и определяющим преобразование энергии разряда в энергию плазмы и работу, совершаемую каналом при расширении:
![]() (4)
(4)
Первое
слагаемое описывает приращение работы, совершаемой расширяющимся каналом, при
изменении его объема ![]() под действием
давления внутри канала Pch. Здесь
под действием
давления внутри канала Pch. Здесь![]() –
энергия плазмы, расширяющейся в адиабатическом приближении с показателем γ.
–
энергия плазмы, расширяющейся в адиабатическом приближении с показателем γ.
Напряженно-деформированное состояние упругопластической среды вокруг канала рассматривалось в сечении, перпендикулярном оси канала, как движение среды по соотношениям [5]:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() ,
(8)
,
(8)
![]() (9)
(9)
![]() (10)
(10)
где
r и R – начальная и текущая координаты элементов среды, ρ,
ρ0, P, u, σi, Si, ![]() , e – текущая и начальная плотность среды,
давление, массовая скорость, напряжения, компоненты девиатора напряжений,
компоненты тензора скоростей деформации, внутренняя энергия единицы массы
среды, μ – модуль сдвига для
данного материала.
, e – текущая и начальная плотность среды,
давление, массовая скорость, напряжения, компоненты девиатора напряжений,
компоненты тензора скоростей деформации, внутренняя энергия единицы массы
среды, μ – модуль сдвига для
данного материала.
Для расчета текучести использовалось условие текучести Мизеса.
В качестве модельной среды выбран гранит с ударной адиабатой:
![]() ,
(11)
,
(11)
где ρ0=2,67 г/см3, сl=5850 м/с — скорость упругой волны, n=2 – константа, характеризующая вещество, μ = 31,6·109 Па, Y=0,25·109 Па – предел текучести.
Энергия деформирования и кинетическая энергия рассчитывались из соотношений:
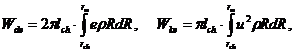 (12)
(12)
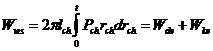 ,
(13)
,
(13)
где rw – радиус области, охваченной распространяющейся волной.
Приведенные уравнения интегрировались численно [5] с нулевыми начальными условиями t=0: R=r, U(r)=0, ρ(r)=ρ0, σi(r)=0, e(r)=0 для r>rch=r0 и граничным условием в виде Pch(t).
Начальный радиус канала принимался 5 мкм. Эффективный показатель адиабаты γ=1,1 [3]. Параметры контура изменялись в диапазонах С=5–20 нФ, U0=250–350 кВ, L=10–25 мкГн, rz =1 Ом. Длина канала lch=0,5–2 см.
Результаты моделирования
Типичные зависимости, иллюстрирующие
преобразование энергии накопителя для трех значений генерирующей емкости
(типичных параметров для электроразрядных технологий), приведены на рисунке 4,
где приняты следующие обозначения: ![]() , объемная
плотность энергии в канале
, объемная
плотность энергии в канале ![]() ,
коэффициенты преобразования энергии в канал
,
коэффициенты преобразования энергии в канал ![]() и
в волну
и
в волну ![]() .
.
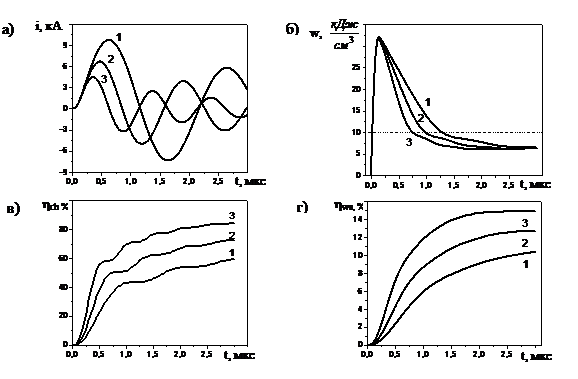
Анализ полученных зависимостей
показывает, что основной этап формирования волны напряжений в твердой среде
заканчивается к концу первого полупериода разрядного тока![]() .
Вторая и последующие токовые пульсации много слабее влияют на энергетику волны.
Это обусловлено двумя причинами. Во-первых, эффективность преобразования
энергии в энергию волны в рассмотренных режимах не превышала 15%. Во-вторых,
разрядный канал является эффективным источником импульсной нагрузки лишь на
начальном этапе разряда (в течение
.
Вторая и последующие токовые пульсации много слабее влияют на энергетику волны.
Это обусловлено двумя причинами. Во-первых, эффективность преобразования
энергии в энергию волны в рассмотренных режимах не превышала 15%. Во-вторых,
разрядный канал является эффективным источником импульсной нагрузки лишь на
начальном этапе разряда (в течение ![]() ). Это следует из рисунка 4 (б), где объемная плотность энергии в плазме
канала сопоставлена с объемной плотностью энергии нитроглицерина
). Это следует из рисунка 4 (б), где объемная плотность энергии в плазме
канала сопоставлена с объемной плотностью энергии нитроглицерина ![]() (штриховая линия) [3]. В это время канал
интенсивно расширяется и генерирует в окружающую среду ударную волну. По мере
расширения канала объемная плотность энергии значительно снижается,
соответственно разрядный канал теряет свойства источника взрывного нагружения.
В связи с этим дополнительный ввод энергии во второй и последующих пульсациях
тока менее эффективен с целью увеличения энергии волны. На рисунке 4 (в, г)
показано изменение двух основных параметров ηch и ηws, определяющих эффективность
преобразования энергии Wg в канал и ударную волну. Видно, что в
течение первого полупериода вводится основная доля энергии Wg. Соответственно этому и волна в
основном формируется в этом временном интервале.
(штриховая линия) [3]. В это время канал
интенсивно расширяется и генерирует в окружающую среду ударную волну. По мере
расширения канала объемная плотность энергии значительно снижается,
соответственно разрядный канал теряет свойства источника взрывного нагружения.
В связи с этим дополнительный ввод энергии во второй и последующих пульсациях
тока менее эффективен с целью увеличения энергии волны. На рисунке 4 (в, г)
показано изменение двух основных параметров ηch и ηws, определяющих эффективность
преобразования энергии Wg в канал и ударную волну. Видно, что в
течение первого полупериода вводится основная доля энергии Wg. Соответственно этому и волна в
основном формируется в этом временном интервале.

С, нФ: 1 – 20, 2 – 10, 3 – 5
Сравнение полученных зависимостей
показывает, что с увеличением емкости накопителя абсолютные величины Wch и Wws растут, но их относительные величины ![]() и
и ![]() снижаются.
Эта закономерность обусловлена менее быстрым ростом Wch и Wws по отношению к Wg.
снижаются.
Эта закономерность обусловлена менее быстрым ростом Wch и Wws по отношению к Wg.
Соответствующие эпюры тангенциальных напряжений в среде и радиальные распределения концентрации энергии деформирования в волне приведены на рисунке 5. Величина еd(R) показывает количество энергии деформирования Wdе, сосредоточенное в объеме данного слоя вещества.
Из эпюр σ2 следует, что
в волне образуется область растяжения, в которой уровень напряжений превосходит
предел прочности гранита на разрыв σ*=8 МПа [6]. Это означает,
что в рассмотренном диапазоне изменения энергии накопителя и параметров
разрядного промежутка в среде возникнут условия для развития радиальных трещин
и разрушения материала. Количество и протяженность трещин в основном будут
определяться характером распределения энергии в волне. Из рисунка 5, б (кривая 1) следует, что наибольшая
концентрация энергии деформирования достигается в окрестности канала. В
области (rch < R ≤ 2,5 мм) величина сжимающих напряжений и концентрация энергии достаточны для переизмельчения среды. По мере
удаления от канала объемная плотность энергии снижается. И для R ≥
R* ≈ 18 мм (рис. 5, б, кривая 1) концентрация энергии в веществе согласно [7] становится ниже плотности
эффективной энергии разрушения е*.
Следовательно, приток энергии в устье трещины будет недостаточен, и ее рост,
вызванный прохождением прямой волны, на этом расстоянии от канала прекратится.
В области 2,5 ≤ R ≤
R*
в зависимости от
величины отношения ![]() возможно прорастание n трещин. Из сравнения распределений
σ2 и еd также следует, что с уменьшением
энергии импульса область растягивающих тангенциальных напряжений образуется
раньше, но уровень соответствующих энергетических характеристик волны
существенно снижается (рис. 5, б, кривые 2, 3) . Это означает, что условия
зарождения трещин реализуются и при относительно небольших энерговкладах в
разряд, но энергии волны для развития сетки протяженных трещин недостаточно.
Результаты выполненного анализа качественно согласуются с экспериментальными
данными [4].
возможно прорастание n трещин. Из сравнения распределений
σ2 и еd также следует, что с уменьшением
энергии импульса область растягивающих тангенциальных напряжений образуется
раньше, но уровень соответствующих энергетических характеристик волны
существенно снижается (рис. 5, б, кривые 2, 3) . Это означает, что условия
зарождения трещин реализуются и при относительно небольших энерговкладах в
разряд, но энергии волны для развития сетки протяженных трещин недостаточно.
Результаты выполненного анализа качественно согласуются с экспериментальными
данными [4].
Выводы
В результате выполненного исследования разработана физико-математическая модель электровзрыва в конденсированной среде, включающая силовой и энергетический критерии разрушения материала. Модель позволяет проследить особенности преобразования энергии емкостного генератора в энергию волновых возмущений, приводящих к разрушению твердых тел. На основании эпюр тангенциального напряжения и распределения концентрации энергии в волне проанализированы условия зарождения и развития радиальных трещин, позволяющие прогнозировать картину разрушения материала.
Работа выполнена в рамках бюджетной программы «Грантовое финансирование научных исследований на 2015-2017 годы», по подприоритету: «Рациональное природопользование и обеспечение равновесного экологического состояния окружающей среды Казахстана», по теме: «Исследование электровзрывного воздействия на конденсированные среды для развития электроразрядных технологий откола и разрушения твердых материалов».
Рецензенты:Важов В.Ф., д.т.н., кафедра электроэнергетических систем Энергетического института Федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский Томский политехнический университет», г. Томск;
Пушкарёв А.И., д.ф.-м.н., кафедра техники и электрофизики высоких напряжений Института физики высоких технологий Федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский Томский политехнический университет», г. Томск.
Библиографическая ссылка
Кузнецова Н.С. ИССЛЕДОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК УДАРНО-ВОЛНОВОГО ПРОЦЕССА ПРИ ЭЛЕКТРОВЗРЫВЕ В ТВЕРДЫХ ТЕЛАХ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=23087 (дата обращения: 11.02.2026).



