Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследования в области решения задач относительно моделирования и прогнозирования инновационных процессов в отраслях экономики показали, что неопределенность, присущая аналитическим задачам, имеет более общую природу, а не одну лишь статистическую.

Во-первых,  необходимо учитывать все возможные факторы, влияющие на поведение объекта. К сожалению, если и можно построить такую модель, используя традиционные методы, то она будет громоздкой и непригодной для практического использования, что связано как с функциональными, так и с экономическими аспектами.

Во-вторых, упрощение модели в рамках традиционных методов неизбежно приведет к неадекватности получаемых решений вследствие недостаточно полного учета факторов неопределенности.

Таким образом, построение точных математических моделей инновационного развития отраслей экономики, пригодных для реализации в прикладном программном обеспечении при решении аналитических задач поддержки и принятия решений, на основе использования традиционных методов, осуществить или трудно, или вообще невозможно.

Альтернативным способом моделирования поведения сложных экономических систем является допущение нечеткости при их описании. Это утверждение основывается на принципе несовместимости. Суть этого принципа заключается в том, что с ростом сложности системы способность делать точные и содержательные утверждения об ее поведении падает до определенной границы, за которой такие характеристики, как точность и содержательность становятся взаимоисключающими [1]. Поэтому абсолютно точный количественный анализ реальных сложных объектов не очень подходит для решения экономических задач.

Таким образом, подход к решению экономических задач поддержки принятия решений должен опираться на то, что ключевыми элементами являются не числа, а некоторые нечеткие множества. Действительно, логика рассуждений человека не является обычной двузначной или даже многозначной логике, это – логика с нечеткими истинами, нечеткими отношениями и правилами вывода. Как ни странно, именно такая нечеткая и не вполне понятная логика является важнейшим компонентом одной из главных особенностей человеческого мышления, а именно способности обобщать информацию, выделять только необходимые данные для решения конкретной задачи. Эта ключевая способность человеческого мышления и позволяет принимать удачные решения ЛПР в конкретных ситуациях. Неучет данного фактора при создании прикладного математического и программного обеспечения прогнозирования во многом определяет недостатки современных технологий и систем принятия экономических решений.

Для реализации эффективного прикладного математического и программного обеспечения технологии решения аналитических задач прогнозирования, принятия экономических решений по управлению сложными динамическими объектами необходимым условием является всесторонний учет неопределенности при формализации и обработке информации. Учет неопределенности информации и его эффективность напрямую зависят от выбора математического инструментария, определяемого математической теорией.

На сегодняшний день можно выделить ряд математических инструментов, предназначенных для формализации неопределенной информации [2]: многозначная логика, теория вероятности, теория ошибок, теория интервальных средних, теория субъективных вероятностей, теория нечетких множеств (теория нечеткой логики).

Одним из наиболее эффективных математических инструментов, направленных на формализацию и обработку неопределенной информации, и во многом интегрирующих известные подходы и методы, является теория нечеткой логики. Данный математический аппарат позволяет с единых позиций рассмотреть различные виды неопределенности и получить новый, качественно более высокий результат.

Нечеткая логика – это совокупность теоретических основ, методов, алгоритмов, процедур и программных средств, базирующихся на использовании нечетких знаний и оценок экспертов для решения широкого круга задач [3].

Использование нечеткой логики эффективно там, где нет возможности четко формализовать данные, где преобладает экспертная лингвистическая вербальная информация. Например, числовые показатели уровня инновационного развития отрасли могут быть представлены неточно, описательно, например, технологический уровень обслуживания оборудования может принимать значения от 20 до 230 % и иметь следующие термы: нереальней 20–80 % (Н); нормальный 80–120 % (НО); высокий 120–150 % (В); очень высокий 150–230 % (ОВ); катастрофически высокий 230 % (К). Для возможности представления такого рода информации определяется функция разделения уверенности в истинности значения числа. Нечеткое число, таким образом, может быть получено словесно, представлено графически в виде функции в двумерной системе.

Это приводит к тому, что числовая величина, которая имеет конкретный физический смысл для эксперта, перестает иметь одно значение (чего требует традиционная математика), а может выражаться набором значений, каждое со своей долей уверенности. При этом доля уверенности отражает влияние и силу возможно действующих факторов. Трактовка нечетких чисел определяется в каждом конкретном случае отдельно и зависит от физической сущности этих чисел, а также от факторов, на них влияющих.

Нечеткие числа, получаемые в результате «не вполне точных измерений», во многом аналогичны распределениям теории вероятностей, но свободны от присущих последним недостатков: малое количество пригодных к анализу функций распределения, необходимость их принудительной нормализации, соблюдение требований аддитивности, трудность обоснования адекватности математической абстракции для описания поведения фактических величин. В границе, при возрастании точности, нечеткая логика приходит к стандартной, Булевой. В сравнении с вероятным методом нечеткий метод позволяет резко сократить объем производимых вычислений, что в свою очередь приводит к увеличению быстродействия нечетких систем [4].

Для прогнозирования уровня инновационного развития отраслей в условиях априорной неопределенности предлагается использовать аппарат теории нечеткой логики, основными преимуществами которой при решении экономических задач являются [3]:

• возможность оперировать входными данными, заданными нечетко: например, значениями, непрерывно изменяющиеся во времени (динамические задачи), значения, которые невозможно задать однозначно (результаты статистических опросов и т.п.);

• возможность нечеткой формализации критериев оценки и сравнения: оперировать критериями «большинство», «возможно», «преимущественно» и т.п.;

• возможность проведения качественного оценивания как входных данных, так и выходных результатов;

• возможность проведения быстрого моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности: оперируя принципами поведения системы, описанными нечеткими методами, во-первых, не тратится много времени на выяснение точных значений переменных и составление уравнений, которые их описывают, во-вторых, можно оценить разные варианты выходных значений.

Все основные показатели, с помощью которых можно определить уровень инновационного развития отрасли, делятся на 2 группы, а именно: показатели, определяющие количественные параметры и характеризующие тенденции в инновационном развитии отрасли, и показатели, с помощью которых отражаются качественные характеристики данной стратегически важной отрасли. При моделировании инновационных процессов в отраслях экономики очень важным является сочетание показателей обеих групп. Особое значение такое сочетание имеет прежде всего для эконометрических моделей; в противном случае они не будут адекватно отражать происходящие инновационные процессы и экономическую ситуацию как такую [5].

Поэтому предлагается целесообразным при моделировании и прогнозировании уровня инновационного развития отраслей экономики объединять в модели как статистические, так и экспертные данные, что является возможным при использовании аппарата теории нечеткой логики [3]. Предложенный метод прогнозирования приведен на рис. 1.

Предложенный метод моделирования и прогнозирования уровня инновационного развития отраслей работает как с количественными данными, так и с качественными (знания экспертов), что является новой разработкой в данной области.

Методы прогнозирования уровня инновационного развития отраслей экономики

                                                                            

 

Рис. 1. Методы прогнозирования уровня инновационного развития отраслей экономики

 

Для решения задачи моделирования и прогнозирования уровня инновационного развития отраслей с нечеткими входными данными и отсутствием аналитической зависимости между входными и выходными параметрами наиболее приспособлен математический аппарат ТНМ (теории нечетких множеств), который позволяет формализовать с помощью математического аппарата нечеткой логики естественные причинно-следственные связи между параметрами. Применение теории нечеткой логики позволяет описать данные связи естественным языком, освобождая исследования от трудоемких процедур сбора и обработки больших массивов экспериментальных данных [4].

Причинно-следственные связи выявляются с помощью специалистов (экспертов в данной области) и представляют собой базу знаний. На основе созданной таким образом базы знаний и предлагается выполнять моделирование и прогнозирование уровня инновационного развития отрасли.

При разработке моделей на базе ТНМ используются следующие основные понятия, предложенные Л. Заде в одной из основных работ по нечеткой логике [1]:

1. Понятие универсального множества. Универсальное множество U – это полное множество, охватывающее всю проблемную область.

2. Нечетким множеством F на универсальном множестве U называется совокупность пар (m F (u), u), где m F (u) – степень принадлежности элемента uÎU нечеткого множества F. Степень принадлежности находится в диапазоне [0,1]. Чем выше степень принадлежности, тем в большей мере элемент универсального множества соответствует свойствам нечеткого множества.

3. Понятие функции принадлежности. Функция принадлежности m F (u) отражает степень принадлежности каждого элемента универсального множества нечеткому подмножеству F. Функция принадлежности приобретает значения от 0 до 1.

Если универсальное множество состоит из конечного числа элементов U = {u1, u2, ..., un}, тогда нечеткое множество F записывается в виде:

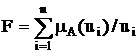                                                                                                              (1)

В случае непрерывного множества U используют такое обозначение:

                                                                                                      (2)

4. Лингвистической переменной называется такая переменная, значение которой являются слова и словосочетания некоторого естественного или искусственного языка.

5. Терм-множеством называется множество всех возможных значений лингвистической переменной.

6. Термом называется элемент терм-множества. В теории нечетких множеств терм задается функцией принадлежности.

Основные операции теории нечетких множеств, используемые для моделирования уровня инновационного развития отраслей, определяются так:

1. Операция дополнения множеств:

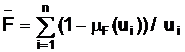                                                                                                             (3)

                                                                                                                       (4)

2. Операция объединения множеств:

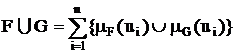                                                                                   (5)

                                                                                         (6)

 

где È – знак оператора взятия максимума.

3. Операция сечения множеств:

                                                                                           (7)

                                                                                                   (8)

где Ç – знак оператора минимума.

С помощью вышеприведенных правил записываются нечеткие логические уравнения. Операции взятия минимума и максимума соответствуют операциям логического “и” и логического “или” в четкой логике.

Имея знания о причинно-следственных связях двух факторов, например: «Если R, то G», использующие нечеткие множества R Ì U, G Ì V, можно выполнить нечеткий логический вывод R  ®  G, R' ®  G', который означает, что если с R факта следует факт G, то из факта R' следует факт G', где R, G, R', G' – нечеткие множества [1]. Это является составлением базы знаний.

С помощью нечеткой базы знаний выполняется аппроксимация зависимости y = f(x1, x2, ... xn), что имеет название нечеткого логического вывода.

Для того чтобы выполнить операцию логического вывода, необходимо знать нечеткое отношение между множествами. Нечеткое отношение между множествами R Ì G і G Ì V, заданные на универсальных множествах: W={w1,w2, ... wl} и V={v1,v2, ... vm}, определяется матрицей, имеющей такой вид:

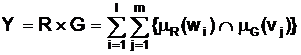                                                                              (9)

В матрице размерностью l ´ m, которую мы получили, элемент, стоящий на пересечении i-й строки и j-го столбца, определяется как:

 

                                                                           (10)

Для расчета логического вывода (G') используем формулу:

G' = R' o Y = R' o (R ´ G),

где o – операция min-max композиции.

Подставив формулу этой операции в (10), получаем:

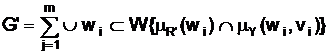                                                                (11)

Применение математического аппарата, основанного на теории нечеткой логики, в вопросах моделирования инновационных процессов в отраслях экономики должно основываться на общенаучных методологических принципах:

1. Принцип лингвистичности переменных системы. В соответствии с этим принципом входные и выходные переменные модели будут рассматриваться как лингвистические переменные с качественными термами (т. е. с теми значениями, которые принимают переменные). Примерами лингвистических термов являются: профессионально-квалификационный потенциал, состояние финансового потенциала, состояние интеллектуального потенциала, состояние информационной среды, состояние производственной среды, состояние ресурсного потенциала.

2. Принцип лингвистичности при принятии конкретных решений. Согласно этому принципу причинно-следственные связи между входными и выходными параметрами системы описываются на естественном языке, а затем формализуются в виде совокупности нечетких логических высказываний “ЕСЛИ-ТО-ИНАЧЕ”.

Совокупность таких высказываний можно рассматривать как набор точек в пространстве «входные параметры – исходный параметр». По этим точкам с использованием нечеткого логического вывода строится поверхность, что дает возможность оценивать значения выходной переменной при таких значениях входных параметров, знание о которых в базе отсутствуют.

3. Принцип иерархичности. При использовании двух первых принципов появляется возможность описать причинно-следственные связи между входными и выходными параметрами. Применение принципа иерархичности позволяет избежать трудностей, связанных с размерностью системы (количеством входных параметров). В соответствии с этим принципом целесообразно провести классификацию входных параметров и по ней построить дерево вывода, определяющее систему вложенных друг в друга высказываний – знаний меньшей размерности, что эквивалентно введению подстановок.

За счет этого принципа можно учитывать практически неограниченное количество входных параметров, влияющих на решение [2]. Таким образом, задача моделирования сводится к следующим этапам:

1. Построение дерева вывода.

2. Определение областей изменения входных параметров.

3. Оценка качественных (лингвистических) параметров.

4. Определение типов решений и областей их изменения.

5. Создание базы знаний.

6. Формализация базы знаний в виде нечетких логических высказываний.

7. Получение системы нечетких логических уравнений.

Разработка моделей функций принадлежности, обеспечивающие представление количественных и качественных параметров в виде нечетких множеств для различного числа лингвистических термов, входящих в базу знаний.

На рисунке 2 представлен граф модели прогнозирования уровня инновационного развития отрасли, в котором показывается зависимость между входящими и выходными параметрами.

 

 

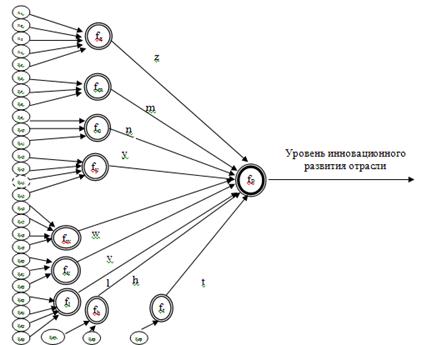
Рис. 2. Модель оценки уровня инновационного развития отрасли

Программная реализация модели может быть осуществлена в среде MATLAB. Нечеткое моделирование в среде MATLAB осуществляется с использованием расширения Fuzzy Logic Toolbox, в котором реализованы десятки функций нечеткого вывода и нечеткой логики [5].

Выводы

Введение разработанной модели оценки и прогнозирования уровня инновационного развития должно  обеспечить адекватное управление инновационными процессами в данной стратегически важной отрасли экономики. Кроме того, указанная модель может рассматриваться как типичная для приведенного класса объектов, а разработанная на ее базе методология моделирования может применяться для других экономических систем, характеризующихся нечеткой связью между входными и выходными параметрами, трудностями формализации факторов влияния и имеют возможность привлечения экспертных знаний для построения модели.

Использование инструмента нечеткой логики при построении прогнозов развития отрасли должно стать составной частью общей методологии управления инновационным развитием.

Рецензенты:

Корецкая Л.К., д.э.н., профессор, профессор кафедры «Экономика и финансы» Владимирского филиала Финуниверситета, г. Владимир;

Дигилина О.Б., д.э.н., профессор, профессор кафедры «Бизнес-информатика и экономика» ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.