При добыче полезных ископаемых в районе вечной мерзлоты существует проблема устойчивости частично протаявших горных пород, в частности целиков, оставляемых в выработках при камерно-столбовой разработке.
Для решения этой проблемы рассмотрим следующую модель мерзлой горной породы: трехмерная, неоднородная анизотропная среда – соответствующая горной породе, с эллипсоидальными неоднородностями, которым соответствуют ледяные включения. Ледяные включения разнесены по пространству горной породы и имеют различные пространственные ориентации. Структурные составляющие горной породы и ледяные включения, испытывающие большие растягивающие напряжения при одноосном сжатии мерзлой породы, будем считать «благоприятно» ориентированными, а не испытывающие растягивающих напряжений – «неблагоприятно» ориентированными.
Эффективный модуль податливости Sэ и эффективный модуль упругости определены следующим образом:
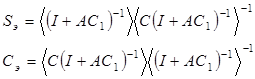 (1)
(1)
где I – единичный тензор,
С – постоянный тензор модуля упругости структурной составляющей,
C1=C-<C> — случайный тензор, постоянный в пределах каждой неоднородности,
![]() – постоянный тензор,
– постоянный тензор,
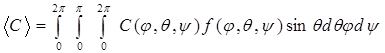 – осредненное значение модуля упругости,
– осредненное значение модуля упругости,
f(j,q,y) – функция распределения структурных составляющих по ориентациям.
Обозначим через e(r) непрерывное внешнее поле деформаций, которое при заданных внешних силах (включая условия на бесконечности) существовало бы при C1=0 в однозначной среде, и через e (r) — кусочно-непрерывное поле деформаций в среде с неоднородностями при таких же внешних условиях.
Используя метод эквивалентного поля (МЭП), изложенный в неявной форме в работах Валпола и Левина [1, 5], и проведя серию преобразований, подробно описанную в работах [2, 3], получим формулу, определяющую эффективный модуль податливости криогенной горной породы.
![]() , (2)
, (2)
где ![]() – эффективный модуль податливости основной среды;
– эффективный модуль податливости основной среды;
![]() – объем породы, приходящийся на одно ледяное включение;
– объем породы, приходящийся на одно ледяное включение;
![]() – концентрация ледяных включений;
– концентрация ледяных включений;
K(R)= -defG0 def – оператор, имеющий ядро ![]()
![]() – функция Грина;
– функция Грина;
![]() – функция распределения ледяных включений по пространству породы.
– функция распределения ледяных включений по пространству породы.
Для построения функции Ф2(R) под интегралом в данном выражении необходимо задаться конкретной моделью случайного поля неоднородностей, т.е. ледяных включений в среде.
Определяя напряжение в рамках того же метода эквивалентного поля, имеем:
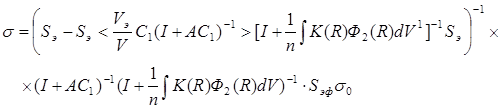 . (3)
. (3)
Поскольку ![]() представляет собой эффективный модуль податливости криогенной горной породы, то, упрощая, (3) запишем в матричном виде:
представляет собой эффективный модуль податливости криогенной горной породы, то, упрощая, (3) запишем в матричном виде:
![]() , (4)
, (4)
где ![]() – единичная матрица
– единичная матрица ![]() ;
;

![]() – эффективный модуль упругости основной среды;
– эффективный модуль упругости основной среды;
![]() – эффективный модуль упругости ледяного включения;
– эффективный модуль упругости ледяного включения;
![]() ,
, ![]() ,
,
Мы получили общее выражение для определения поля напряжений в криогенных горных породах.
Произведены численные расчеты si(jqy) через ![]() по всем углам Эйлера для угля шахты «Центральная» Сангарского месторождения. Для наглядности полученные значения представлены в виде графиков (1, 2, 3, 4). Заметим, что величины касательных напряжений на два порядка меньше, чем величины нормального напряжения s2, поэтому нецелесообразно изображать их на графике.
по всем углам Эйлера для угля шахты «Центральная» Сангарского месторождения. Для наглядности полученные значения представлены в виде графиков (1, 2, 3, 4). Заметим, что величины касательных напряжений на два порядка меньше, чем величины нормального напряжения s2, поэтому нецелесообразно изображать их на графике.
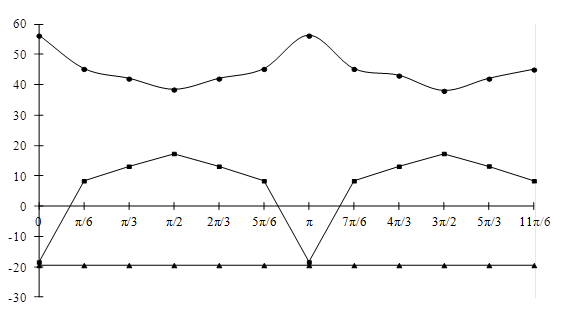
Рис. 1. График зависимости тензоров напряжения ![]() ледяного включения от его пространственной ориентации
ледяного включения от его пространственной ориентации
● --- ![]() , ■ ---
, ■ --- ![]() , ▲ ---
, ▲ --- ![]()
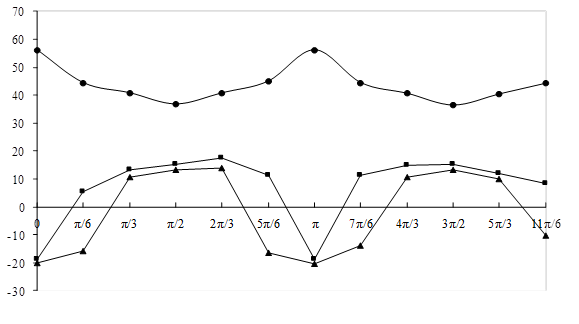
Рис. 2. График зависимости тензоров напряжения ![]() ледяного включения от его пространственной ориентации
ледяного включения от его пространственной ориентации
● --- ![]() , ■ ---
, ■ --- ![]() , ▲ ---
, ▲ --- ![]()
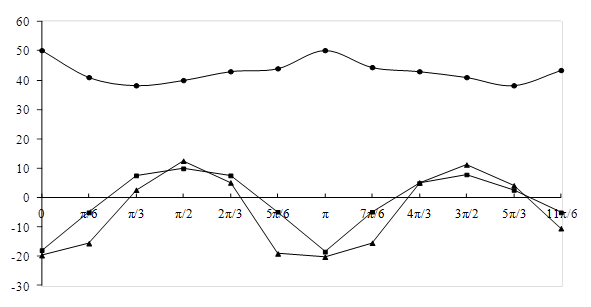
Рис 3. График зависимости тензоров напряжения ![]() ледяного включения от его пространственной ориентации
ледяного включения от его пространственной ориентации
● --- ![]() , ■ ---
, ■ --- ![]() , ▲ ---
, ▲ --- ![]()
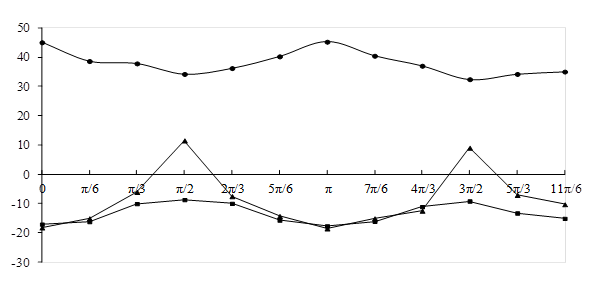
Рис. 4. График зависимости тензоров напряжения ![]() ледяного включения от его пространственной ориентации.
ледяного включения от его пространственной ориентации.
● --- ![]() , ■ ---
, ■ --- ![]() , ▲ ---
, ▲ --- ![]()
Из графиков очевидно, что предел прочности породы зависит от преимущественной ориентации текстурных составляющих:
1) «благоприятно» ориентированные текстурные составляющие испытывают растягивающие напряжения - s1 и - s2, превосходящие по величине предел прочности их на растяжение;
2) менее «благоприятно» ориентированные текстурные составляющие испытывают растягивающие напряжения - s1 и - s2, равные пределу прочности на растяжение;
3) «неблагоприятно» ориентированные текстурные составляющие вовсе не испытывают растягивающих напряжений;
4) есть текстурные составляющие, испытывающие растягивающие напряжения либо - s1, либо - s2 равные или превосходящие предел прочности на растяжение.
В связи с изложенным за критерий разрушения текстурных составляющих принимается критерий максимального растягивающего напряжения, несмотря на то, что мерзлая порода в целом испытывает одноосное сжатие.
Расчеты были сделаны для шахты «Центральная» Сангарского угольного месторождения. Предел прочности мерзлого угля можно считать равным sсж=225·105 Па, что на 25% больше предела прочности того же угля при умеренной положительной температуре. Однако при преимущественной горизонтальной ориентации ледяных включений предел прочности может доходить до sсж=280·105 Па, что видно из графиков, а при преимущественной вертикальной ориентации предел прочности уменьшается до sсж=162·105 Па [4].
Таким образом, мы показали:
1) зависимость упругих свойств криогенных горных пород (на примере мерзлого угля) от упругих характеристик и концентрации ледяных включений, рассчитав эффективный упругий модуль характерного объема породы путем осреднения по всем реализациям случайного поля ледяных включений с учетом их концентрации и пространственной ориентации;
2) зависимость напряжений, наблюдаемых в криогенной горной породе, от концентрации ледяных включений и величины внешних напряжений, учитывая влияние ориентации ледяных включений на величину и характер испытываемых ими напряжений.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы, по ГК № П 1105, ГК № П 1122 от 02.06.2010 г.
Рецензенты:
Боташев А.Ю., д.т.н., профессор, профессор кафедры «Технологические машины и переработка материалов» ФГБОУ ВПО «Северо-Кавказская государственная гуманитарно-технологическая академия», Министерство образования и науки РФ, г. Черкесск;
Борлаков Х.Ш., д.ф.-м.н., профессор, профессор кафедры общеинженерных и естественнонаучных дисциплин ФГБОУ ВПО «Северо-Кавказская государственная гуманитарно-технологическая академия», Министерство образования и науки РФ, г. Черкесск.
Библиографическая ссылка
Кидакоев А.М., Шайлиев Р.Ш., Биджиев С.Х., Кидакоев А.М., Лепшоков Р.А., Лепшокова С.А. ОБ ОДНОЙ МОДЕЛИ НАПРЯЖЕННОСТИ НЕОДНОРОДНОЙ АНИЗОТРОПНОЙ СРЕДЫ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22961 (дата обращения: 06.02.2026).



