Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследование на разрешимость неклассических краевых задач для обыкновенных дифференциальных уравнений второго порядка и разработка численных методов их решения приводит к необходимости получения оценок решений локальных краевых задач для этих уравнений.

Аналогичная проблема возникает при решении краевых задач для нагруженных дифференциальных уравнений в дифференциальной и конечно-разностной постановках.

            В настоящей работе исследуется поведение решения краевой задачи третьего рода

,   0<x<1,(1)

(2)

,                 (3)

где 

   всюду на [0.1] , а  положительные числа. Как известно [3,4],задача  (1)-(3) однозначно разрешима в классе функции , при этом имеет место априорная оценка

       .                                               (4)

            В данной работе будет получена поточечная оценка решения задачи (1)-(3), а также априорная оценка, усиливающая (4).

Приведем необходимые сведения для решения поставленной задачи. 

Рассмотрим два уравнения:

                             (5)

(6)

где функции  и вещественны и непрерывны на интервале  и

.(7)

При этих условиях уравнение (6) называется мажорантой Штурма[5] для уравнения (5) на J.

Теорема 1. Пусть коэффициенты уравнений (5) и (6) непрерывны на (], и пусть уравнение (6)является мажорантой Штурма (5). Предположим, что  и  являются решениями уравнений (5) и (6)  соответственно, всюду на отрезке []  удовлетворяет соотношениям:

,      ,

и в точке выполнено неравенство

Тогда

,   .(8)

Доказательство теоремы приводится в [1].

Для получения оценки (5) будем пользоваться [4] представлением решения задачи (1)-(3) в виде

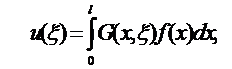.        (9)

где   – функция Грина третьей краевой задачи.

Функция   определяется по формуле

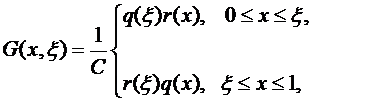(10)

гдеr(x), q(x)-решения задач

,        0<<1,                               (11)

,

 

                           (12)

а постоянная C в (9) определяется по формуле

           

Введем обозначение  и изучим свойства решений задач (11) и (12). Лемма.1Пусть k()

Тогда решение задачи (11)будет положительной, строго возрастающей на [0,1] функцией. При этом для всех  имеет место неравенство

(13)

                  Для доказательства неравенства (13) применим теорему 1, приняв в неравенстве (8) в качестве  решение  задачи (11), а в качестве - решение  задачи

          (14)

В силу неравенств,  уравнение (11) является мажорантой Штурма уравнения (14). Единственным  решением задачи (14) является функция

,

которую,используя левое краевое условие (11), перепишем в виде

(15)

                  Поскольку числа 𝜆, , , ,  положительны, то нетрудно показать, что  будет положительной, строго возрастающей на [0,1] функцией. Очевидно, что

Таким образом, выполнены все условия теоремы 1. Подставляя в (8) функции  и  вместо  и  и учитывая, что в данном случае

,

приходим к неравенству

 .                             (16)

Оценим снизу . Используя краевые условия в (11), получаем:

откуда,с учетомравенства

имеем

.

Из цепочки неравенств 

следует, что

(17)

Пользуясь (15) и (17) из (16) получаем неравенство  (13).

Лемма 2. Пусть  всюду на . Тогда решение задачи (12) на отрезке [0,1]будет положительной, строго убывающей функцией. При этом имеет место неравенство

.(18)

 

Доказательство леммы 2 проводится по аналогии [2]с доказательством леммы 1.

Теорема 2. Пусть k()

0< всюду на [0,1]. Тогда для решения задачи (1)-(3) имеет место оценка

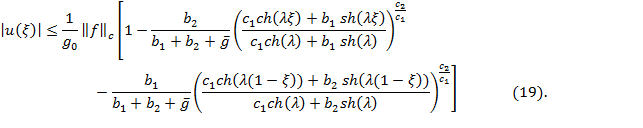
Для доказательстватеоремывоспользуемся представлением (9)решения задачи (1)-(3) с помощью функции Грина:

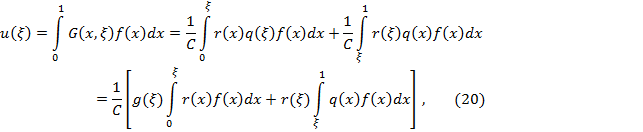
где  и- решения задач (11) и (12).

Заметим, что:

а);  (21)

б);(22)

Тогда

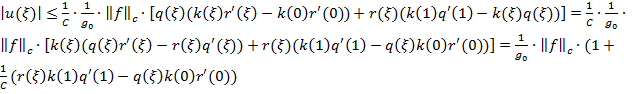.        (23)

Воспользуемся краевыми условиями в  (11) ,(12).Учитывая, что из (23)

получаем оценку:

.(24)

Из оценок (24), (13) и (18) следуетоценка решения в точке ξ:

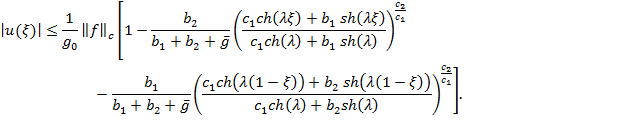
С учетом свойств  функцийиз последнего получаем априорную оценку решения:

.

Рецензенты:  

Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления   Кабардино-Балкарского научного центра РАН, г. Нальчик;

Ашабоков Б.А., д.ф.-м.н., профессорВысокогорного геофизического института, г. Нальчик.