Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В диагностике различных болезней и оценке функционального состояния организма важная роль принадлежит определению размеров, формы и плотности органов и тканей. В этой связи технология электроимпедансной томографии обладает значительным потенциалом. Применение электроимпедансной томографии позволяет избавить человека от комплекса болевых и неприятных ощущений, исключает лучевую нагрузку на организм и внесение во внутреннюю среду болезнетворных вирусов и бактерий, чужеродных веществ (например, эндоскопические процедуры).

Повсеместное применение ЭИТ в клинической практике позволит решить ряд медико-социальных задач, повысить качество медицинских услуг, уменьшить затраты лечебно-профилактических учреждений на оснащение современным медицинским оборудованием и, как следствие, сделать медицинскую помощь доступнее населению.

Электроимпедансная томография (ЭИТ) представляет собой неинвазивный метод визуализации проводимостей внутренних структур биологических объектов (БО).Для получения томографического среза БО подвергается зондированию высокочастотным электрическим током малой амплитуды (различной формы). При прохождении тока через БО создается разность потенциалов между различными точками на поверхности объекта. С помощью специального математического аппарата реконструкции и визуализации распределения электрического импеданса внутри БО строятся томографические изображения БО [1].

СообществомисследователейразработанпакетпрограммEIDORS[11] (Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software). В данном программном продукте реализованы следующие алгоритмы реконструкции: алгоритм Гаусса-Ньютона [2], алгоритм двойной начальной внутренней точки [3], алгоритм полной вариации [5] с использованием метода двойной начальной внутренней точки [3], алгоритм сопряженных градиентов [7],алгоритм усеченного сингулярного разложения [7].

В пакете  EIDORSзаложена возможность статической (абсолютной) и динамической (дифференциальной) реконструкции [11]. При статической реконструкции используется один набор данных, и по ним реконструируется распределение проводимости в объекте в момент измерения. При дифференциальной реконструкции используется два набора данных для двух моментов времени и реконструируется изменение проводимости в объекте между начальным и конечным моментом времени. Реализовать статическую реконструкцию сложнее, т.к. одному набору данных могут соответствовать множество распределений проводимости.

В пакете EIDORS реализованы различные алгоритмы реконструкции, однако практически все они имеют ряд параметров, влияющих на результат реконструкции. Основными параметрами, существенно влияющими на результат реконструкции, являются число элементов сетки конечных элементов, метода определения регуляризирующего оператора [6], значение гиперпараметра (используется для баланса при контроле соответствия данным и соответствия априорному распределению [12]) и значение начальной проводимости.

Также в программном продукте реализован автоматический подбор гиперпараметра путем вычисления усиления шума алгоритмом. Оптимальным являетсягиперпараметр, при котором усиление шума алгоритмом минимально. Однако данная функция очень чувствительна к параметрам модели и входным данным, а также сильно увеличиваетсся время вычислений в силу итерационности процесса. Также расчет усиления шума алгоритмом реализован не для всех алгоритмов.

Чем ближе значение начальной проводимости к значению проводимости исследуемого объекта, тем точнее реконструкция [9].

Таким образом, необходимо определить оптимальное число элементов сетки, алгоритм реконструкции и значение гиперпараметра для этого алгоритма, а также метод расчета регуляризирующего оператора.

Для этого в пакете EIDORS [11] была создана прямая конечноэлементная модель с двумя неоднородностями σ1 и σ2. Проводимость объекта σ3. Проводимость неоднородностей в 2 раза выше проводимости объекта. Объект – единичная окружность. Координаты первой неоднородности [0;0,5], второй [-0.5; -0.5]. Сетка конечных элементов генерируется стандартной функцией среды Octave – distmesh. Distmesh генерирует треугольную нерегулярную сетку конечных элементов. Параметры разбиения задаются с помощью пакета EIDORS [11]. Одному набору параметров может соответствовать несколько вариантов разбиения. Для избавления влияния разбиения на результат моделирования при одинаковом числе электродов были созданы сетки конечных элементов для каждого числа электродов, которые затем использовались для дальнейших исследований. Использовались наборы параметров b2d1c,c2d1c,d2d1c, e2d1c, f2d1c, j2d1c [11]. Первая буква определяет плотность сетки (по возрастанию), 2d – указатель размерности модели и способа разбиения (двумерная, distmesh), следующее число определяет уточнение элементов (увеличивает число элементов сетки), последняя буква – указатель формы модели (c – circular - круглая). Для данных параметров были получены сетки со следующим числом элементов: 499; 1230; 2983; 4567; 5198; 10487.

Для определения степени схожести реконструированного и оригинального изображения использовался коэффициент ковариации [4]. Расчет проводился встроенной функцией пакета Octave – corrcoef. Вычислялся коэффициент корреляции двух массивов данных, соответствующих проводимости элементов сетки для оригинального и реконструированного изображений. Однако данный метод невозможно использовать для определения оптимального числа элементов сетки конечных элементов, т.к. коэффициент корреляции будет максимален для минимального числа элементов (с увеличением числа элементов сетки увеличивается число несовпадений). Поэтому для определения оптимального числа элементов сетки будем определять относительное число элементов, значение которых отличается от элементов оригинала больше чем на ±5%.  Расчет велся по формуле (1).

  ,                                                          (1)

где Nотн – относительное число элементов, превысивших значение оригинала больше чем на ±5%, Nвер – число элементов, удовлетворяющее условию, N – число элементов сетки.

Исследование числа элементов сетки проводилось при 16 электродах, протокол измерения Sheffieldprotocol (два соседних электрода инжектирующие, измеряется разность потенциалов между остальными соседними электродами [10]). Модель для 16 электродов на 2983 элемента показана на рисунке 1а. Оригинальное изображение реконструируемого распределения проводимости приведено на рисунке 1б. Шкала на рисунке показывает соответствие цвета и проводимости. Красным показана область с высокой проводимостью, синим – с низкой.

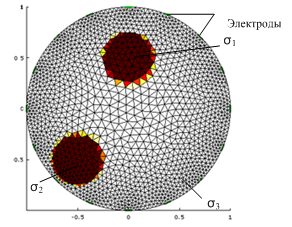
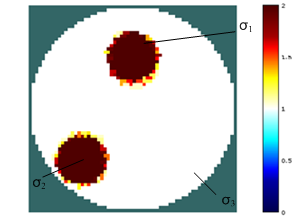
а)                                                                    б)

Рис. 1.Конечноэлементая модель (а) и оригинальное изображение (б) в среде EIDORS

Реконструкция производилась с помощью алгоритма Гаусса-Ньютона [2]. Метод Ньютона-Гаусса — это итерационный численный метод нахождения решения задачи наименьших квадратов. Является разновидностью метода Ньютона. Этот метод использует матрицу Якобиана производных первого порядка функции  для нахождения вектора значений параметра, который минимизирует остаточные суммы квадратов (сумму квадратных отклонений предсказанных значений от наблюдаемых). Т.к. автоматический подбор гиперпараметра не реализован для данного алгоритма, реконструкция проведена для 5 значений гиперпараметра (0,1;0,01;0,001;0,0001;0,00001). Полученные результаты сведены в таблицу 1.

Таблица 1

Результаты расчетов

На рисунке 2 представлен график зависимости относительного параметра от числа элементов сетки при различных значениях гиперпараметра.

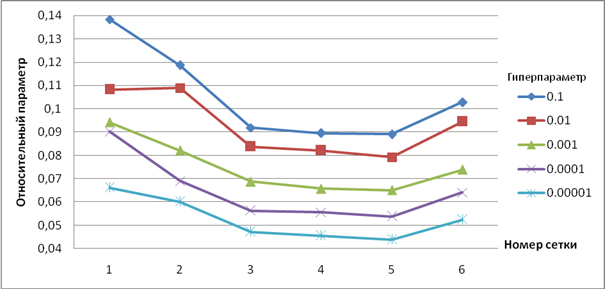
Рис.2. Зависимости относительного параметра от числа элементов сетки при различных значениях гиперпараметра

Как видно из рисунка 2, относительный параметр, демонстрирующий точность реконструкции (чем меньше параметр, тем меньше элементов реконструированного изображения превышают соответствующий элемент оригинального изображения больше чем на ±5%), уменьшается с увеличением числа элементов. Однако при слишком большом числе элементов точность реконструкции уменьшается. Это может быть связано с накапливанием ошибок округления при большом числе элементов [8]. Минимальное значение относительного параметра соответствует набору параметров f2d1c (5198) элементов сетки, однако приведенная разность между данным значением и значением при параметрах сетки d2d1c (2983 элемента) не превышает 5%. При этом увеличение числа элементов пропорционально увеличивает время вычисления. Время расчета ограничено техническим заданием. Таким образом, в качестве оптимального числа элементов выберем число элементов 2983, соответствующее набору параметров сетки d2d1c.

Для выбранных параметров сетки проведена реконструкция изображения разными алгоритмами. При наличии возможности варьировался метод определения регуляризирующего оператора (для некоторых алгоритмов возможно использовать только специализированный регуляризующий параметр, для некоторых при изменении регуляризующего параметра степень изменения результата реконструкции составляет 10-6).

Лучшие результаты реконструирования сведены в таблицу 2. Из таблицы видно, что оптимальным алгоритмом для дальнейших исследований является статический алгоритм Гаусса-Ньютона.

Таблица 2

Результаты сравнения алгоритмов реконструкции распределения проводимости

 

Таким образом, найдены оптимальные параметры сетки конечных элементов, выбран оптимальный алгоритм реконструкции, метод определения регуляризующего оператора, значение гиперпараметра для данного алгоритма. Полученные данные используются для определения оптимального числа электродов, оптимальной амплитуды тока для электроимпедансной томографии.

Рецензенты:

Гречихин В.В., д.т.н., доцент, профессор кафедры ИИСТ, ФГБОУ ВПО «ЮРГПУ(НПИ) им. М.И. Платова», г. Новочеркасск;

Кириевский Е.В., д.т.н., доцент, профессор кафедры ИИСТ, ФГБОУ ВПО «ЮРГПУ(НПИ) им. М.И. Платова», г. Новочеркасск.