Необходимость изучения краевых задач для дифференциальных уравнений дробного порядка связана с тем, что многие проблемы теории фильтрации жидкости во фрактальной среде, фильтрации жидкости в трещиноватой среде с фрактальной геометрией трещин приводят к дифференциальным уравнениям дробного порядка. Дробные производные применяются при описании физических процессов стохастического переноса, изучении деформационно-прочностных свойств полимерных материалов. Численным методам решения уравнения диффузии дробного порядка в многомерных областях посвящены работы [3, 8]. Задачи, когда на границе области помещена сосредоточенная теплоемкость некоторой величины, рассмотрены в [4]. В работе [7] построена локально-одномерная схема для многомерного уравнения теплопроводности с сосредоточенной теплоемкостью. В [2] рассмотрен случай многомерной задачи и построена локально-одномерная схема для уравнения диффузии дробного порядка, когда на границах области по каждому направлению помещена сосредоточенная теплоемкость некоторой величины.
1. ПОСТАНОВКА ЗАДАЧИ. УСТОЙЧИВОСТЬ
В области ![]()
![]() рассматривается краевая задача для обобщенного уравнения диффузии с сосредоточенной теплоемкостью вида:
рассматривается краевая задача для обобщенного уравнения диффузии с сосредоточенной теплоемкостью вида:
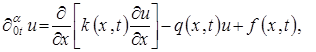
![]() , (1)
, (1)
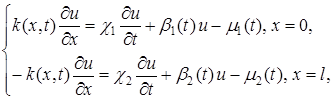 (2)
(2)
![]() ,
, ![]() , (3)
, (3)
где коэффициенты удовлетворяют условиям ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ,
, 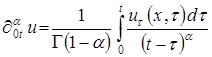 – регуляризованная производная дробного порядка
– регуляризованная производная дробного порядка ![]() [6].
[6].
Для доказательства устойчивости решения задачи (1)-(3) будем пользоваться методом энергетических неравенств. После умножения уравнения (1) скалярно на ![]() получаем энергетическое тождество:
получаем энергетическое тождество:
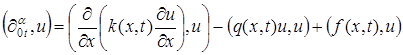 , (4)
, (4)
где 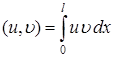 , норма
, норма 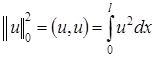 .
.
Для второго скалярного произведения в правой части (4), интегрируя по частям с учетом краевых условий (2), будем иметь:
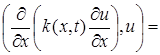
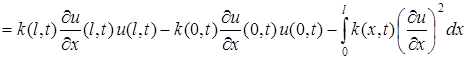
![]()
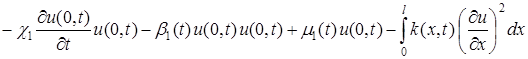 . (5)
. (5)
Используя лемму 1 ([1], стр. 152) и учитывая условия на коэффициенты ![]() и
и ![]() , из (5) получим:
, из (5) получим:
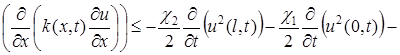
![]() .
.
Для третьего интеграла в энергетическом тождестве (4) с учетом условия ![]() запишем:
запишем:
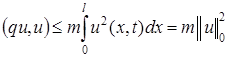 .
.
Последнее скалярное произведение в тождестве (4) оценим с помощью ![]() -неравенства. Для
-неравенства. Для ![]() будем иметь:
будем иметь:
![]() .
.
С учетом полученных неравенств из (4) имеем:
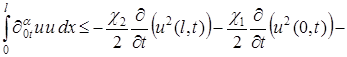
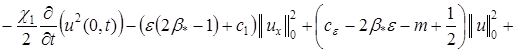
![]() . (6)
. (6)
Интегрируя (6) по ![]() от 0 до
от 0 до ![]() , получаем:
, получаем:
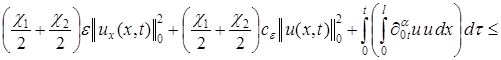
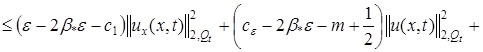
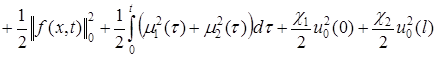 .
.
Пренебрегая положительным интегралом, получаем неравенство:
![]()
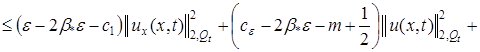
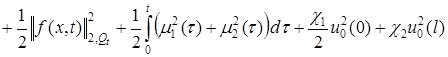 . (7)
. (7)
Обозначим в последнем неравенстве ![]() и потребуем, чтобы
и потребуем, чтобы ![]() . Будем иметь:
. Будем иметь:
![]()
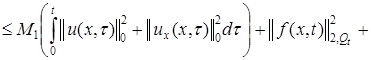
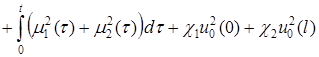 . (8)
. (8)
Применяя лемму 1 для нестационарных задач ([1], стр. 152), из последнего получим:
![]()
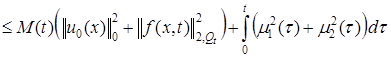 , (9)
, (9)
где ![]() – положительная величина, зависящая от коэффициентов уравнения и размеров области
– положительная величина, зависящая от коэффициентов уравнения и размеров области ![]() . Из априорной оценки (9) следует устойчивость решения задачи (1)-(3) по входным данным задачи, а также его единственность.
. Из априорной оценки (9) следует устойчивость решения задачи (1)-(3) по входным данным задачи, а также его единственность.
2. РАЗНОСТНАЯ СХЕМА
В замкнутой области ![]()
![]() строится сетка
строится сетка ![]() , где
, где ![]() – шаг сетки
– шаг сетки ![]() по переменной
по переменной ![]() ,
, ![]() – шаг сетки
– шаг сетки ![]() по переменной
по переменной ![]() ,
, ![]() ,
, ![]() ;
; ![]() – число разбиений по переменной
– число разбиений по переменной ![]() ;
; ![]() – число разбиений по переменной
– число разбиений по переменной ![]() .
.
Для задачи (1)-(3) построена разностная схема:
![]() (10)
(10) 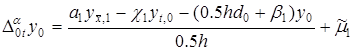 ,
, ![]() (11)
(11)
![]() ,
, ![]() (12)
(12)
![]() ,
, ![]() ,
, ![]() (13)
(13)
Здесь ![]() ,
, ![]() ,
, ![]() ,
, 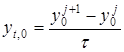 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
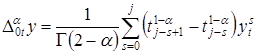 – разностный аналог дробной производной
– разностный аналог дробной производной ![]() , и в классе достаточно гладких функций справедливо равенство
, и в классе достаточно гладких функций справедливо равенство ![]() [9].
[9].
3. УСТОЙЧИВОСТЬ РАЗНОСТНОЙ СХЕМЫ
Для доказательства устойчивости разностной схемы (10)-(13) используем принцип максимума. Для этого схему приводим к каноническому виду [5]:
![]() (14)
(14)
где ![]() – связная сетка;
– связная сетка; ![]() – окрестность узла
– окрестность узла ![]() , не содержащая самого узла
, не содержащая самого узла ![]() . Для коэффициентов (14) должны выполняться условия:
. Для коэффициентов (14) должны выполняться условия:
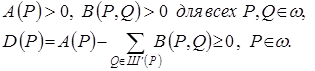 (15)
(15)
Расписав (10) в индексной форме с учетом ![]()
![]() в точке
в точке ![]() получим:
получим:
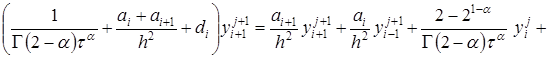
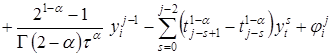 . (16)
. (16)
Сравнивая (16) с (14), видим:
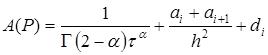 ,
, ![]() ,
,  .
.
Так как по условию ![]() , то
, то
![]() ,
, ![]() ,
, ![]() (17)
(17)
Здесь ![]() .
.
В точке![]() , расписывая (11) в индексной форме, будем иметь:
, расписывая (11) в индексной форме, будем иметь:
 . (18)
. (18)
Ввиду условий ![]() ,
,![]() ,
, ![]() имеем:
имеем:
![]() ,
, ![]() ,
, ![]() . (19)
. (19)
Аналогично, в точке ![]() для граничного условия (12) имеем:
для граничного условия (12) имеем:
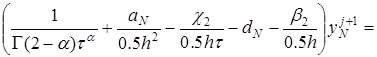
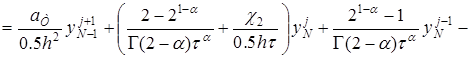
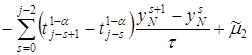 . (20)
. (20)
С учетом условий ![]() ,
,![]() ,
, ![]() имеем:
имеем:
![]() ,
, ![]() ,
, ![]() . (21)
. (21)
Из неравенств (17), (19), (21) на основании теоремы 3 [5] для задачи (10)-(13) верна оценка:
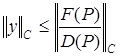 , (22)
, (22)
из которой следует устойчивость решения разностной схемы (10)-(13).
Рецензенты:
Шхануков-Лафишев М. Х., д.ф.-м.н., профессор ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН, г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного Геофизического Института, г. Нальчик.
Библиографическая ссылка
Нахушева Ф.М., Кудаева Ф.Х., Кайгермазов А.А., Кармоков М.М. РАЗНОСТНАЯ СХЕМА ДЛЯ УРАВНЕНИЯ ДИФФУЗИИ ДРОБНОГО ПОРЯДКА С СОСРЕДОТОЧЕННОЙ ТЕПЛОЁМКОСТЬЮ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22638 (дата обращения: 11.02.2026).



