Пассивные системы виброзащиты (подрессоривания) с постоянными характеристиками транспортных средств являются наиболее распространенными в настоящее время. Потенциальные возможности подобных систем виброзащиты в удовлетворении требований к плавности хода транспортных средств ограниченны. В связи с этим пассивные системы сдерживают повышение виброзащиты водителя, комфортности пассажиров, сохранности перевозимых грузов, виброзащиты собственных агрегатов и узлов транспортного средства и препятствуют росту эксплуатационных скоростей его движения. В связи с этим создание управляемых систем виброзащиты с целью повышения плавности хода транспортных средств является актуальной проблемой; одним из путей ее решения является построение электромеханических виброзащитных систем [1; 4].
Цель исследования
Целью данных исследований является рассмотрение возможностей повышения демпфирующих свойств системы пассивной виброзащиты за счет дополнения ее управляемым электромагнитным элементом (группой управляемых электромагнитных элементов различной конструкции).
Материалы и методы исследования
В качестве амортизирующих конструкций в системах амортизации объектов могут быть использованы: пружинные, гидравлические, пневмогидравлические, пневматические, инерционные, резиновые, пластические амортизаторы. Опыт эксплуатации систем амортизации крупногабаритных объектов показал, что весьма перспективными являются пневматические упругие элементы на основе резинокордной оболочки. В таких опорах отсутствует металлический контакт между подрессоренными и неподрессоренными частями амортизируемого объекта и передача вибрационных нагрузок осуществляется через резинокордную стенку и сжатый рабочий газ [1; 2].
Такой амортизирующий элемент имеет множество достоинств, таких как высокая грузоподъемность, низкая цена, плавность хода автотранспортных систем на основе этого элемента.
Для исследования виброзащитной системы рассмотрены свободные колебания в одностепенной системе. Свободные колебания АО и давление рабочего газа пневмоамортизатора (ПА) с электромагнитным компенсатором описываются следующей математической моделью [3]:
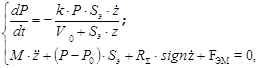 (1)
(1)
где Р – текущее давление рабочего газа (воздуха) в резинокордной оболочке,
![]() - давление в резинокордной оболочке ПА при статическом положении;
- давление в резинокордной оболочке ПА при статическом положении;
![]() - высота подъема АО;
- высота подъема АО;
![]() - рабочий объем ПА при статическом положении АО;
- рабочий объем ПА при статическом положении АО;
![]() ,
, ![]() - масса амортизированного объекта и ускорение силы тяжести;
- масса амортизированного объекта и ускорение силы тяжести;
![]() - показатель адиабаты;
- показатель адиабаты;
![]() - эффективная площадь ПА;
- эффективная площадь ПА;
![]() - относительные перемещения, скорость и ускорение АО;
- относительные перемещения, скорость и ускорение АО;
Rå - сила трения в РКО,
Fэм - электромагнитная сила, развиваемая компенсатором.
В случае пассивной виброзащитной системы Fэм = 0 Н.
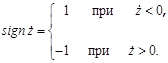 (2)
(2)
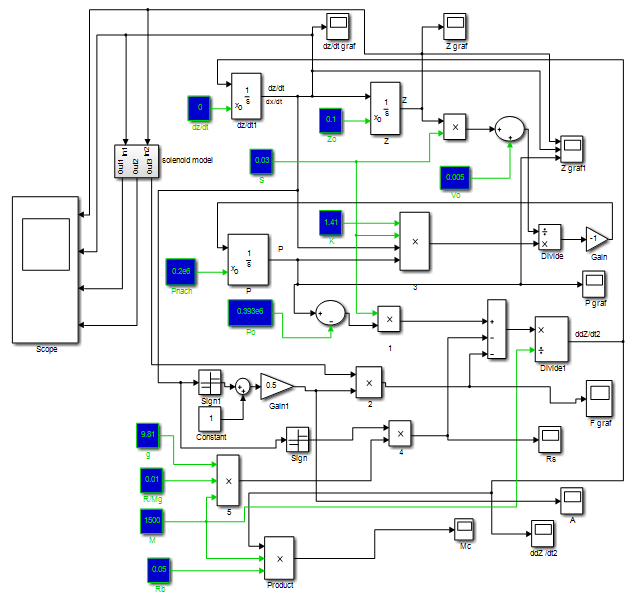
Рис. 1. Модель электромагнитного демпфера с компенсатором жесткости
При составлении уравнений приняты следующие допущения.
1. Рабочий газ в ПА подчиняется законам идеальных газов.
2. Температура окружающей среды постоянна и равна Тс.
3. Рабочий процесс в ПА считается адиабатическим.
4. Движение АО происходит только в вертикальном направлении.
5. Эффективная площадь (Sэ) ПА при движении АО не меняется.
6. Утечки газа из ПА отсутствуют.
7. R∑ = 0,01 Mg (для случая примененной резинокордной оболочки Н-48, определено экспериментально).
В процессе исследования была создана модель пневмоамортизатора [5; 6] в программном комплексе Matlab-Simulink (рис. 1). Начальные условия для системы: при ![]()
![]() = 0,1 м,
= 0,1 м, ![]() . В модель введена модель соленоида в качестве компенсатора жесткости, который создает расчетное противодействующее усилие упругой силе пневмоамортизатора. Время включения компенсатора жесткости определяется производной от перемещения груза: по производной определяются экстремумы функции перемещения груза, т.е. при положительном значении производной груз идет вверх, компенсатор жесткости включается, при смене знака производной производится отключение устройства (рис. 2).
. В модель введена модель соленоида в качестве компенсатора жесткости, который создает расчетное противодействующее усилие упругой силе пневмоамортизатора. Время включения компенсатора жесткости определяется производной от перемещения груза: по производной определяются экстремумы функции перемещения груза, т.е. при положительном значении производной груз идет вверх, компенсатор жесткости включается, при смене знака производной производится отключение устройства (рис. 2).
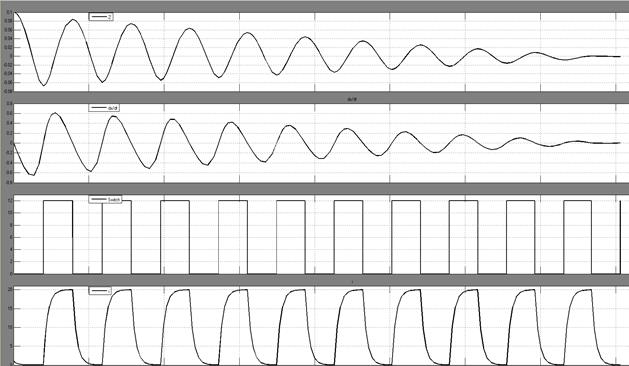
Рис. 2. Графики перемещения, скорости, включения компенсатора жесткости и тока в соленоиде соответственно
Математическая модель соленоида [2] описывает процессы в электрической подсистеме на основе уравнения, составленного по второму закону Киргоффа:
![]()
![]()
![]()
![]() (3)
(3)
где �� – номинальное напряжение питания соленоида,
R – сопротивление катушки соленоида,
L(x) – индуктивность катушки соленоида,
i – ток в катушке соленоида,
x – координата перемещения сердечника соленоида,
![]() – потокосцепление катушки соленоида.
– потокосцепление катушки соленоида.
На основе магнитного сопротивления магнитной цепи соленоида определим его индуктивность в виде зависимости от координаты перемещения сердечника соленоида:
![]()
![]()
![]() (4)
(4)
где Rm – магнитное сопротивление системы,
![]() – магнитная проницаемость вакуума,
– магнитная проницаемость вакуума,
N – число витков катушки соленоида,
L – индуктивность соленоида,
a – толщина магнитопровода,
d – ширина воздушного зазора в магнитопроводе,
g – величина воздушного зазора между сердечником и катушкой.
Электромагнитная сила определяется в предположении линейной магнитной системы и постоянства тока при изменении координаты перемещения сердечника соленоида:
![]()
![]() (5)
(5)
![]() – энергия магнитного поля соленоида.
– энергия магнитного поля соленоида.
Расчет производился с конструкцией соленоида, представленной на рисунке 3.
Сравним различные конструкции соленоидов с помощью программного комплекса «Elcut 5.1 Профессиональный» (табл. 1). Рассмотрим три различные конструкции (рис. 3): без магнитопровода (а), с магнитопроводом (б), с магнитопроводом с раздельными обмотками, включенными последовательно (в, г). Варианты В и Г различаются количеством обмоток (2 или 3 соответственно). Все конструкции разработаны с учетом оптимальных массогабаритных параметров, определенных техническим заданием.
Таблица 1
Сравнение усилий, развиваемых соленоидом при различных конструкциях
|
Расстояние, на которое выдвинут сердечник, мм |
Развиваемое усилие, Н |
|||
|
Одна обмотка, без магнито-провода |
Одна обмотка, с магнито-проводом |
Две обмотки, с магнито-проводом |
Три обмотки, с магнито-проводом |
|
|
10 |
8,06 |
148,91 |
6,54 |
70,36 |
|
35 |
2 |
8.14 |
22,68 |
201,95 |
|
45 |
1.66 |
6.43 |
158,62 |
68,26 |
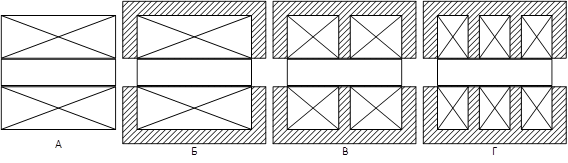
Рис. 3. Исследуемые конструкции компенсаторов жесткости: А – без магнитопровода, Б – с магнитопроводом, В, Г – с магнитопроводом и раздельными катушками
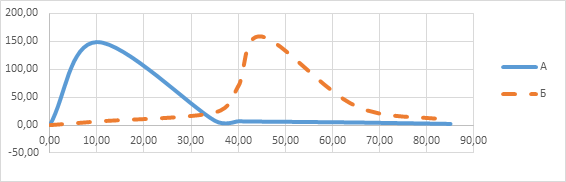
Рис. 4. Графики усилий, развиваемых соленоидом в зависимости от вылета сердечника: А - с одной катушкой и магнитопроводом, Б – с двумя катушками и дополнительным участком магнитопровода
Как видно из сравнения – наибольшее усилие в малом диапазоне развивает соленоид, состоящий из одной катушки и магнитопровода.
Вывод
Для расширения диапазона можно использовать два параллельно работающих соленоида с различной конфигурацией обмоток (рис. 3). Таким образом, используя два параллельно работающих компенсатора жесткости, можно добиться более ровной характеристики усилия и уменьшения времени колебания колебаний. Так, при использовании одного устройства с однокатушечным соленоидом время гашения колебаний составляет 8,06 секунды, а при использовании двух устройств (с однокатушечным соленоидом и с соленоидом с расщепленной обмоткой), работающих параллельно, время сокращается до 6 секунд.
Рецензенты:
Кузнецов А.А., д.т.н., проф., зав. кафедрой «Теоретическая электротехника» ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск;
Хацевский К.В., д.т.н., проф., кафедра «Электротехника и оборудование» Омского института водного транспорта, г. Омск.
Библиографическая ссылка
Демин А.В., Хамитов Р.Н. ИССЛЕДОВАНИЕ КОНСТРУКЦИЙ ЭЛЕКТРОПНЕВМАТИЧЕСКОГО ВИБРОЗАЩИТНОГО УСТРОЙСТВА СОЛЕНОИДНОГО ТИПА // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22484 (дата обращения: 11.02.2026).



