Надежность и экономичность систем пневмотранспорта зависят от правильного выбора скорости транспортирующего воздушного потока. Повышение этой скорости сокращает срок службы пневмопроводов, ведет к увеличению потерь давления в сети и расхода электроэнергии, а ее снижение вызывает выпадение транспортируемого материала в пневмопроводе и его закупоривание. На скорость транспортирования оказывает влияние концентрация перемещаемого материала в воздушном потоке. Но оценка этого влияния в работах разных авторов различается [3]. С помощью численного моделирования выполнен расчет изотермического турбулентного воздушного потока, воздействующего на шарообразные частицы, расположенные в воздуховоде круглого сечения. Результаты расчета позволяют оценить влияние концентрации материала на давление на частицы при постоянной скорости воздушного потока.
Цель исследования
Методами математического моделирования выполнить анализ воздействия турбулентного воздушного потока на шарообразные частицы, расположенные в воздуховоде круглого сечения. Провести оценку влияния концентрации материала на давление на частицы при постоянной скорости воздуха.
Метод исследования
Моделирование турбулентного течения проводилось с помощью трехмерных уравнений Навье—Стокса, осредненных по Рейнольдсу (ReynoldsAreragedNavier—Stokes, или RANS):
уравнение сохранения массы
![]() , (1)
, (1)
уравнение сохранения импульса
![]() , (2)
, (2)
тензор вязких напряжений ![]() , определен с помощью реологического закона Ньютона
, определен с помощью реологического закона Ньютона
![]() , (3)
, (3)
а тензор турбулентных напряжений ![]() – в соответствии с обобщенной гипотезой Буссинеска
– в соответствии с обобщенной гипотезой Буссинеска
![]() , (4)
, (4)
Для нахождения характеристик турбулентности использована k-ε модель турбулентности:
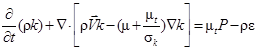 , (5)
, (5)
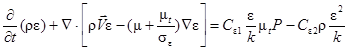 , (6)
, (6)
генерационный член в уравнениях переноса (5) и (6)
![]() , (7)
, (7)
где k — кинетическая энергия турбулентности; ε — скорость диссипации− кинетической энергии турбулентности; µt – турбулентная вязкость; Сε1, Сε2 — полуэмпирические коэффициенты модели турбулентности.
Данный подход моделирования турбулентности является в настоящее время наиболее широко используемым при решении практических задач [2] и позволяет получить трехмерные поля скорости и давления по объему воздуховода, трения и давления на твердые поверхности частиц. Анализ полей показывает сложную структуру взаимодействия потоков в трубе при обтекании систем шарообразных частиц.
В расчетах использовалась k-ε модель турбулентности. Дискретизация исходных уравнений осуществлялась методом контрольного объема. Поля скорости и давления рассчитывались с помощью процедуры PISO [4] в сочетании с многосеточным алгоритмом AMG [5].
В процессе математического моделирования изучены особенности формирующегося вблизи частиц скоростного поля и распределение давления по поверхности частиц. Для определения суммарной силы давления на частицы вычислялся интеграл давления по их поверхности.
Постановка задачи
С помощью пакета STAR-CCM+ рассчитать поле скорости воздуха в воздуховоде, заполненной различным количеством частиц, и давления по поверхности частиц.
Принимаем трубу диаметром 0,075 м, длиной 1,5 м. Располагаем частицы на расстоянии 0,5 м от входа в трубу. Диаметр частиц принят 0,005 м. Построены 9 вариантов моделей, в которых количество частиц варьируется от 1 до 200, также меняется их взаимное расположение (табл. 1).
Таблица 1
Количество и взаимное расположение частиц
|
№ модели |
Количество шарообразных частиц |
Расположение частиц в трубе |
|
1 |
1 |
- |
|
2 |
3 |
друг за другом |
|
3 |
5 |
упорядоченно |
|
4 |
21 |
хаотичное |
|
5 |
28 |
хаотичное |
|
6 |
42 |
хаотичное |
|
7 |
100 |
хаотичное |
|
8 |
150 |
хаотичное |
|
9 |
200 |
хаотичное |
В созданной модели масса частиц не учитывалась. Скорость воздуха на входной границе принята как разность между скоростью воздушного потока и скоростью частиц, на основании литературного обзора [1] и экспериментальных исследований. Таким образом, скорость воздуха в трубе на входе принята 5 м/с, на выходе — свободный выход воздуха, т.е. давление на выходе равно атмосферному, и воздух выходит без помех. Температура воздуха и плотность воздуха постоянные.
Для повышения точности расчета использовалась неструктурированная сетка с измельчением в области шарообразных частиц (рис. 1). Вблизи стенок трубы и частиц сделаны призматические слои с соответствующим сгущением к поверхностям.

Рис. 1. Расчетная сетка
Количество ячеек в расчетной сетке для различных задач находится в диапазоне от 531 тыс. ячеек для одной частицы, до 1240 тыс. ячеек для 42 частиц. Особое внимание уделено разрешению сеточной структуры и качеству расчетной сетки. В области частиц выполнено сгущение расчетной сетки. Кроме того, на внутренних стенках трубы и поверхности частиц (рис. 2) был построен призматический слой для описания пристеночных течений.

Рис. 2. Фрагменты расчетной сетки
Результаты расчетов
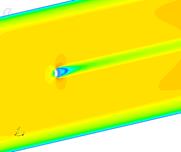
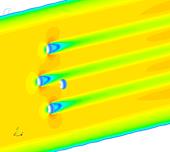
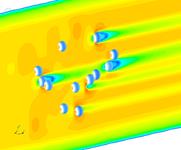
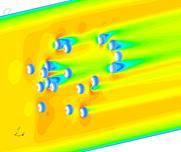
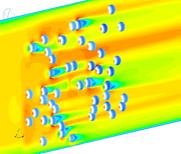
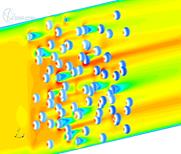
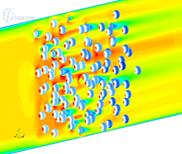
В результате расчетов получены поля скоростей и давления, формирующиеся в трубе (рис. 3). На рисунке 3 поля давлений представлены на шарообразных частицах, а поля скоростей – в пространстве между шариками.
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
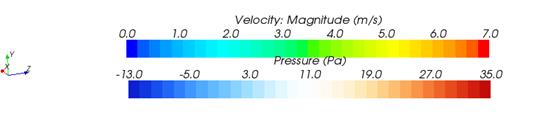
Рис. 3. Поля скоростей воздуха и давления на частицы
Оценка результатов исследования позволяет сделать вывод, что с ростом количества частиц скорость воздуха в живом сечении увеличивается с 5 м/с до 7 м/с. Полное давление на отдельную частицу также возрастает.
Обработка данных
Получены суммарные силы давления на каждую частицу как интеграл давления по поверхности.
Рассмотрим подробнее, какое давление оказывает воздух на частицы (табл. 2). Вводим понятие относительного давления
![]() (8)
(8)
где P – давление на частицу, Н; P0 – давление на частицу в первой модели, P0 =1,816·10-4 Н.
Таблица 2
Давление воздушного потока на частицы
|
№ модели |
Количество шарообразных частиц |
Минимальное относительное давление на частицу |
Максимальное относительное давление на частицу |
Доля частиц с относительным давлением больше единицы, % |
|
1 |
1 |
1 |
1 |
- |
|
2 |
3 |
0,763 |
0,930 |
- |
|
3 |
5 |
1,019 |
1,037 |
- |
|
4 |
21 |
0,791 |
1,058 |
- |
|
5 |
28 |
0,801 |
1,149 |
46 |
|
6 |
42 |
0,467 |
1,713 |
31 |
|
7 |
100 |
0,898 |
1,277 |
54 |
|
8 |
150 |
0,910 |
1,37 |
70 |
|
9 |
200 |
0,945 |
1,470 |
88 |
Максимальное давление на отдельные частицы возрастает в 1,5 раза при одинаковой скорости в воздуховоде.
Вывод
При постоянной скорости воздушного потока с увеличением концентрации материала скорость в пространстве между частицами и давление на отдельную частицу увеличиваются. Следовательно, можно обеспечить необходимое для транспортирования монодисперсных частиц правильной формы давление на частицы, при большой концентрации снизив скорость воздуха в воздуховоде.
Рецензенты:
Уляшева В.М., д.т.н., доцент, профессор кафедры теплогазоснабжения и вентиляции, ФГБОУ ВПО «Санкт-Петербургский архитектурно-строительный университет», г. Санкт-Петербург;
Гримитлин А.М., д.т.н., профессор, Президент НП «СЗ Центр АВОК», г. Санкт-Петербург.
Библиографическая ссылка
Мартьянова А.Ю. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ВОЗДЕЙСТВИЯ ВОЗДУШНОГО ПОТОКА НА ШАРООБРАЗНЫЕ ЧАСТИЦЫ В ВОЗДУХОВОДЕ КРУГЛОГО СЕЧЕНИЯ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22466 (дата обращения: 11.02.2026).