В рамках Государственной программы развития сельского хозяйства и регулирования рынков сельскохозяйственной продукции, сырья и продовольствия на 2013-2020 годы к первому уровню приоритетов государственной политики в сфере развития продовольственного потенциала относится мелиорация земель сельскохозяйственного назначения.
Устойчивое развитие агроресурсного потенциала агроландшафта в современных условиях ведения сельского хозяйства не может эффективно выполняться без комплексных мероприятий охраны земель от различных видов деградаций [1]. Технологии в недостаточной мере учитывают природный ресурс, антропогенные факторы, которые приводят к деградации почв, что приводит к потере конкурентоспособности получаемой продукции. Следовательно, необходимо создание такой системы охраны сельскохозяйственных земель от различного рода деградаций и изменения внешней среды, которая могла бы обеспечивать устойчивое развитие сельского хозяйства.
Как показали исследования в области мелиорации и охраны земель, применение отдельных видов мероприятий не всегда эффективно решает задачи повышения агроресурсного потенциала агроландшафтов. В КубГАУ для решения проблемы сохранения агроресурсного потенциала агроландшафтов (АРП) разработан сельскохозяйственный мелиоративный комплекс [1]. Сельскохозяйственный мелиоративный комплекс – система природоохранных мероприятий, направленных на восстановление, охрану агроресурсного потенциала агроландшафтов и сохранение почвенной среды от загрязнений с помощью ресурсосберегающих и адаптированных технологий для получения высоких и конкурентных урожаев сельскохозяйственных культур.
Охрана природного потенциала земель требует постоянного контроля над мелиоративным состоянием земель, где целью мониторинга следует считать получение достоверной информации по ресурсам при своевременной обработке информации о состоянии развития неблагоприятных процессов.
В области комплексной оценки качества земель ведутся работы по теоретическому обоснованию основных положений методики оценки их качества, включающих оценки по комплексу показателей – физических, гидрохимических, гидробиологических [1]. Следует подчеркнуть, что обоснование критериев оценки качества земель, объема и характера исходной информации должно исходить из концепции сохранения экологического благополучия почв, при котором обеспечивается устойчивость экосистемы и её нормальное функционирование.
Любая мелиоративная работа требует привлечения разнообразных ресурсов (множество ресурсов, необходимых для выполнения определенной работы, будем называть комплексным ресурсом задачи). Составляющие комплексного ресурса имеют самую различную природу: они могут быть информационными, материальными, трудовыми, энергетическими, земельными. Выполнение работы может быть осуществлено с помощью различных наборов компонент комплексного ресурса [2].
Необходимо определить оптимальный перечень мелиоративных работ, обеспечивающий максимальную эффективность мелиорации при заданных ограничениях на капиталовложения и другие ресурсы.
Эффективность отдельных работ будем характеризовать с помощью числовых оценок вклада в достижение общей цели развития мелиорации. К количественным характеристикам отнесем показатели затрат ресурсов и ожидаемые результаты мелиорации.
Рассмотрим построение [2] частной оценки ![]() трудности достижения требуемого качества j-ой компоненты комплексного ресурса с учетом требований, предъявляемых к этой компоненте. Обозначим через
трудности достижения требуемого качества j-ой компоненты комплексного ресурса с учетом требований, предъявляемых к этой компоненте. Обозначим через ![]() и
и ![]() соответственно безразмерную характеристику достигнутого качества и требование к качеству j-ой компоненты комплексного ресурса. Следует подчеркнуть, что нормативные требования носят региональный характер.
соответственно безразмерную характеристику достигнутого качества и требование к качеству j-ой компоненты комплексного ресурса. Следует подчеркнуть, что нормативные требования носят региональный характер.
Будем считать, что ![]() и
и ![]() , j=1,2,…m. Требование к качеству по j-й компоненте выполнено, если
, j=1,2,…m. Требование к качеству по j-й компоненте выполнено, если ![]() . Причем
. Причем ![]() соответствует идеальное качество, а
соответствует идеальное качество, а ![]() - предельно низкое качество по j-й компоненте. Величина
- предельно низкое качество по j-й компоненте. Величина ![]() называется абсолютной оценкой качества j-ой компоненты ресурса.
называется абсолютной оценкой качества j-ой компоненты ресурса.
При ![]() этим условиям удовлетворяет единственная функция вида [2]:
этим условиям удовлетворяет единственная функция вида [2]:
![]() . (1)
. (1)
Доопределим функцию (1) следующим образом:
![]() при
при ![]() ;
; ![]() при
при ![]() .
.
Итак, оценка ![]() характеризует степень выполнения требований, предъявляемых к качеству ресурса и может трактоваться как обобщенная мера степени риска недостижения требуемого качества на основе сопоставления значения показателя качества и нормативного ограничения.
характеризует степень выполнения требований, предъявляемых к качеству ресурса и может трактоваться как обобщенная мера степени риска недостижения требуемого качества на основе сопоставления значения показателя качества и нормативного ограничения.
В работе [5] рассматривается вероятностная интерпретация частных оценок ![]() по j-му показателю качества. Требование к интегральному качеству выполнимо, если
по j-му показателю качества. Требование к интегральному качеству выполнимо, если ![]() . Причем, если качество
. Причем, если качество ![]() ОС хотя бы по одному показателю качества ниже соответствующего порогового значения
ОС хотя бы по одному показателю качества ниже соответствующего порогового значения ![]() , то удовлетворить требования к интегральному качеству невозможно.
, то удовлетворить требования к интегральному качеству невозможно.
Пусть А – событие, состоящее в том, что не выполнено требование к интегральному качеству, а ![]() - событие, состоящее в том, что не выполнено требование к качеству мелиоративного состояния ОС по j-му показателю,
- событие, состоящее в том, что не выполнено требование к качеству мелиоративного состояния ОС по j-му показателю, ![]() - событие, противоположное
- событие, противоположное ![]() . Тогда
. Тогда ![]() - вероятность невыполнения требований к качеству мелиоративного состояния РОС при условии, что требования к качеству выполнены по j-му показателю:
- вероятность невыполнения требований к качеству мелиоративного состояния РОС при условии, что требования к качеству выполнены по j-му показателю:
![]() (2)
(2)
Обозначим ![]() ;
; ![]() - вероятность некачественности по j-му показателю,
- вероятность некачественности по j-му показателю, ![]() - вероятность некачественности мелиоративного состояния ОС по j-му показателю при условии, что требования к ОС не выполнены. Тогда видно, что формула (2) совпадает с формулой (1) частной оценки качества по j-му показателю. В силу вероятностной природы величины
- вероятность некачественности мелиоративного состояния ОС по j-му показателю при условии, что требования к ОС не выполнены. Тогда видно, что формула (2) совпадает с формулой (1) частной оценки качества по j-му показателю. В силу вероятностной природы величины ![]() ,
, ![]() ,
, ![]() принимают значения из отрезка [0;1].
принимают значения из отрезка [0;1].
Событию ![]() соответствует неопределенность (энтропия информации), равная
соответствует неопределенность (энтропия информации), равная ![]() , а противоположному событию
, а противоположному событию ![]() - информационная оценка:
- информационная оценка:
![]() (3)
(3)
Из (3) следует, что ![]() при
при ![]() ;
; ![]() при
при ![]() .
.
Величины ![]() выражают информацию о значимости j-го ресурса в процессе достижения мелиоративного состояния ОС. Потому можно рассматривать
выражают информацию о значимости j-го ресурса в процессе достижения мелиоративного состояния ОС. Потому можно рассматривать ![]() как универсальные стоимостные характеристики единицы j-го ресурса и использовать их в роли коэффициентов линейной целевой функции в оптимизационной модели.
как универсальные стоимостные характеристики единицы j-го ресурса и использовать их в роли коэффициентов линейной целевой функции в оптимизационной модели.
Нами предлагается методика определения вероятности события ![]() , состоящего в невыполнении требования к качеству мелиоративного состояния по j-му показателю.
, состоящего в невыполнении требования к качеству мелиоративного состояния по j-му показателю.
Деградация почвы является следствием нарушения определенных условий, которые задаются требованиями к характеристикам функционирования почвы. Список почвенных показателей чрезвычайно обширен: морфологические, физические, химические, минералогические, биохимические и др. Показатели стохастичны – определяются суммарным вкладом многих факторов, разнообразными комбинациями элементарных почвенных процессов.
Рассмотрим, как оценить вероятность несоблюдения определенного требования по предлагаемой методике. Выбор объективных показателей мелиоративного состояния оросительной системы связан с обоснованием методики локальной числовой оценки качества почв. Под локальной числовой оценкой Z понимается функция от набора показателей, характеризующая качество почвы в конкретной точке и в момент проведения измерений показателей х1, х2, … хi..
Z = φ (х1, х2, ... хi), (4)
Комплексная численная оценка F(S) орошаемой территории S определяется по данным измерений показателей состава и свойств почвы в определенных точках и является функцией от локальных числовых оценок в характерных точках на определенный момент времени.
F(S) = F(Z1, Z2, ... ZN), Zn = φ (х1(n), х2(n), ... хi(n)), n = 1, 2, ... N (5)
Нами предлагается в методологию составления мелиоративно-гидрогеохимических прогнозов ввести оценку экологической обстановки, используя статистический подход при учете реальной пространственно-временной изменчивости показателей состава и свойств почв [3]. Будем рассматривать величину F(S) функцией случайной выборки наблюдений, что позволит с выбранным уровнем достоверности характеризовать степень соответствия экологической обстановки действующим нормативам. Постановка статистической задачи состоит в следующем: имея ряд локальных оценок Z1, Z2, … ZN качества почвы, полученных по данным наблюдений в характерных точках на определенный момент времени, а также зная нормативную границу Zнорм (интервалы изменения Zнорм), требуется с заданной доверительной вероятностью g оценить вероятность Р(Z ≤ Zнорм) соблюдения нормативного качества почв. В указанной постановке задача обобщенной оценки состояния почв практически эквивалентна задаче выборочного контроля качества промышленных изделий в условиях крупносерийного производства.
Если бы была известна достоверная функция распределения ![]() (Z) вероятности значений локальной оценки Z, то искомая вероятность соблюдения нормативного качества почвы определялась также достоверно, то есть с доверительной вероятностью
(Z) вероятности значений локальной оценки Z, то искомая вероятность соблюдения нормативного качества почвы определялась также достоверно, то есть с доверительной вероятностью ![]() = 1. Но конечная выборка наблюдений позволяет получить только приближенную функцию распределения
= 1. Но конечная выборка наблюдений позволяет получить только приближенную функцию распределения ![]() (Z) и, следовательно, приближенно вычислить вероятность соблюдения нормативного качества почв
(Z) и, следовательно, приближенно вычислить вероятность соблюдения нормативного качества почв
P (Z![]() Zнорм) = Ф(Zнорм)
Zнорм) = Ф(Zнорм)
Приближенная оценка (5) характеризует некоторое возможное неблагоприятное состояние почв. Более благоприятному состоянию почв соответствует большая вероятность соблюдения нормативного качества. Следовательно, величина Ф(Zнорм) как выборочная характеристика возможного неблагоприятного состояния с установленной доверительной вероятностью ![]() не должна превосходить генеральную характеристику
не должна превосходить генеральную характеристику
P [Ф(Zнорм) <![]() (Zнорм)] =
(Zнорм)] = ![]() (6)
(6)
Равенство (6) является условием для выбора приближенной функции распределения из множества возможных вариантов, а выражение (4) можно рассматривать как обобщенную оценку состояния почвы по нижней доверительной границе вероятности соблюдения нормативного качества. При этом величина ![]() = 1-
= 1- ![]() есть вероятность или риск принять ошибочное заключение о благополучном состоянии почв в то время, как на самом деле оно было хуже. Вычисления величины Ф(Zнорм) проводим по следующим рассуждениям [4]. Пусть на обследуемой территории проведено N наблюдений и получена однородная выборка локальных оценок качества почвы, которые упорядочены и перенумерованы в порядке ухудшения качества Z1
есть вероятность или риск принять ошибочное заключение о благополучном состоянии почв в то время, как на самом деле оно было хуже. Вычисления величины Ф(Zнорм) проводим по следующим рассуждениям [4]. Пусть на обследуемой территории проведено N наблюдений и получена однородная выборка локальных оценок качества почвы, которые упорядочены и перенумерованы в порядке ухудшения качества Z1 ![]() Z2
Z2 ![]() … Zn
… Zn ![]() Zn+1… ZN. Пусть
Zn+1… ZN. Пусть
Zn![]() Zнорм
Zнорм![]() Zn+1 и
Zn+1 и ![]() (Zнорм) = q
(Zнорм) = q
Тогда вероятность обнаружить такую выборку описывается биномиальным распределением
![]() (7)
(7)
Из определения (6) следует, что нижняя доверительная граница Рn соответствует такому значению генеральной характеристики q, при котором вероятность получить количество n благоприятных исходов по данным наблюдений, равна β = 1- γ. Значит, уравнение для определения нижней доверительной границы можно представить в следующем виде:
1-![]() =
= 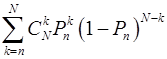 (8)
(8)
Решая уравнение (9), можно определить Рn и, следовательно, найти искомую приближенную функцию распределения
Ф(Zn![]() Z < Zn+1) = Рn=
Z < Zn+1) = Рn= ![]() , 1<n<N; (9)
, 1<n<N; (9)
Ф(Z<Z1) = 0; Ф(Z>ZN)=РN = (1-![]() )1/N (10)
)1/N (10)
Численные значения нижней доверительной границы Рn определяются при помощи таблицы коэффициента R, которая составляется для установленного значения ![]() . Значения R для
. Значения R для ![]() = 0, 95 приведены в [2].
= 0, 95 приведены в [2].
Так как исходная информация имеет вероятностный характер, то целесообразно за основную характеристику качественного состояния почв принять вероятность события Рn, состоящего в том, что качество почвы по данным случайной выборки окажется не хуже заданного класса j.
Величина Рn, зависящая от трёх переменных ![]() , N и n, является непараметрической статистической оценкой степени соответствия почв нормативным условиям.
, N и n, является непараметрической статистической оценкой степени соответствия почв нормативным условиям.
Практическая полезность такой характеристики определяется тем, что по величине Рn можно непосредственно сравнивать состояние почв различных участков в различные периоды времени (чем больше Рn, тем качество почв лучше). Кроме того, по своему определению величина Рn равна относительной части почвенного участка, загрязнённость которой не выходит за пределы класса качества j.
Интегральная оценка, удовлетворяющая требованиям ассоциативности и коммутативности, если частные оценки являются равноценными и одноуровневыми, имеет вид [2]:
![]() , (11)
, (11)
где ![]() - интегральная оценка качества по совокупности частных оценок,
- интегральная оценка качества по совокупности частных оценок, ![]() - весовой коэффициент.
- весовой коэффициент.
Минимальным значениям ![]() соответствует наиболее высокая степень выполнения требований к качеству. Таким образом, изложенная модель интегрального критерия качества может быть использована при разработке систем поддержки принятия управленческих решений и пакета прикладных программ информационно-вычислительного комплекса, предназначенного для оперативного управления мелиоративным состоянием оросительной системы.
соответствует наиболее высокая степень выполнения требований к качеству. Таким образом, изложенная модель интегрального критерия качества может быть использована при разработке систем поддержки принятия управленческих решений и пакета прикладных программ информационно-вычислительного комплекса, предназначенного для оперативного управления мелиоративным состоянием оросительной системы.
Функционирование сельскохозяйственного мелиоративного комплекса в заданном режиме может выполняться только на системном уровне с включением подсистемы (природная среда – земельные и водные ресурсы), которая опирается на уровни (технологии), а уровни – на подуровни системы (процессы, обеспечивающие баланс веществ агроресурсного потенциала ландшафта и повышение мелиоративного состояния почвы). В процессы подсистемы включены адаптированные, ресурсосберегающие технологии, которые обеспечивают воспроизводство природной среды с учетом различных почвенных условий и введенных ограничений по выбору схем отвода избыточных вод и адаптированного подбора мелиоративной техники для их реализации.
Рецензенты:
Свистунов Ю.Ф., д.т.н., профессор, зав. кафедрой комплексных систем водоснабжения, ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар;
Кузнецов Е.В., д.т.н., профессор, зав. кафедрой гидравлики и сельскохозяйственного водоснабжения, ФГБОУ ВПО «Кубанский государственный аграрный университет», г. Краснодар.
Библиографическая ссылка
Сафронова Т.И., Хаджиди А.Е., Холод Е.В. ОБОСНОВАНИЕ МЕТОДА УПРАВЛЕНИЯ АГРОРЕСУРСНЫМ ПОТЕНЦИАЛОМ АГРОЛАНДШАФТОВ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22376 (дата обращения: 28.02.2026).



