С использованием ab-initio программного кода CRYSTAL, основанного на теории функционала плотности, исследованы структурные, электронные и упругие свойства 17 полухейслеровских соединений A1B2X5. Полухейслеровские кристаллы типа A1B2X5 являются аналогами бинарных алмазоподобных соединений типа A3X5 со структурой сфалерита (структура типа ZnS, группа симметрии F-43m). Для всех соединений, проведена процедура оптимизации геометрии кристалла. Вычисленные значения постоянных решетки и ширины запрещенной зоны могут быть использованы в качестве основной информации при подборе перспективных для практического применения материалов. Вычисленные упругие постоянные показывают, что исследованные материалы являются механически стабильными при обычных условиях. Установлено, что большинство материалов являются хрупкими. Вычисленные значения микротвердости сопоставимы с микротвердостями бинарных аналогов A3X5 со структурой сфалерита (ZnS): AlN, AlP и AlAs.
Полухейслеровские (half-Heusler) соединения вида A1B2X5 (где A и B - элементы I и II группы периодической системы, а X - элементы V группы) являются широким классом материалов, перспективных для применения в различных приборах и устройствах. Данные кристаллы обладают высокой температурной стабильностью и могут применяться, например, при производстве солнечных элементов. Актуальной является задача повышения работоспособности гетероструктуры ZnO/CdS/CuInSe2 путем подбора буферного слоя между окном (ZnO) солнечного элемента и его поглощающим слоем (CuInSe2), который давал бы минимум потерь энергии и был бы экологически безвредным, для этой цели может быть использована группа соединений A1B2X5 [4, 5].
Ранее в работах [1-3] мы исследовали электронную структуру полухейслеровских кристаллов вида LiBX (B=Mg, Ca, Zn; X=N, P, As), где в частности, изучили особенности формирования в них зонной структуры, плотности состояний и химической связи.
В настоящей работе в рамках теории функционала плотности представлены результаты расчета ширины запрещенной зоны Eg, упругих свойств и фононных частот для 17 полухейслеровских кристаллов: LiBX (где B=Be, Mg, Ca, Zn; X=P, As), NaBX (где B=Mg, Ca, Zn; X=P, As), AgBX (где B=Mg, Ca; X=P, As) со структурой сфалерита.
Кристаллическая структура, метод и параметры расчета
Полухейслеровские кристаллы типа A1B2X5 (рис.1) являются аналогами бинарных алмазоподобных соединений типа A3X5 со структурой сфалерита (структура типа ZnS, группа симметрии F-43m). Кристаллическая ячейка содержит 3 атома (одна формульная единица). Атомы в элементарной ячейке занимают следующие позиции: A=(0.5,0.5,0.5), B=(0,0,0) и X=(0.25,0.25,0.25), выраженные в единицах постоянной решетки a.
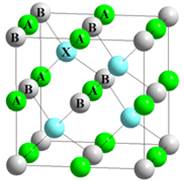
Рис. 1. Структура полухейслеровских соединений A1B2X5
Вычисление электронной структуры исследуемых соединений A1B2X5 осуществлялось в рамках теории функционала плотности DFT, составляющей основу программного кода CRYSTAL. Для расчетов использовали гибридный метод B3LYP и расширенный валентно-расщепленный базис контрактированных гауссовых орбиталей TZVP (Triple-Zeta Valence).
Параметры кристаллической структуры a для большинства соединений AIBIIXV брались нами из теоретических работ. Для кристаллов LiCaAs и AgCaAs значение параметра решетки вычислялось по формуле:
![]() (1)
(1)
где rA, rB, rX атомные ковалентные радиусы элементов, входящих в состав соединения.
Для всех исследуемых кристаллов была проведена стандартная процедура оптимизации геометрии, заложенная в программном коде CRYSTAL. Вычисленное таким образом значение параметра решетки гипотетического кристалла LiCaAs было определено нами в работе [2]. Полученные в результате оптимизации значения равновесных параметров кристаллической решетки a приведены в таблице 1.
Таблица 1
Параметры кристаллической решетки a, Å и ширина запрещенной зоны Eg, эВ (dir – кристалл прямозонный, ind – кристалл непрямозонный) соединений A1B2X5
|
Соединение |
a, Å наш расчет |
a, Å эксперимент |
a, Å [4] |
Eg, эВ наш расчет |
Eg, эВ эксперимент |
|
LiBeP |
5.309 |
- |
5.368 [5] |
4.4 (dir) |
- |
|
LiMgP |
5.928 |
6.005 [9] |
6.019 |
2.7 (ind) |
2.43 [9] |
|
LiCaP |
6.488 |
- |
6.506 |
2.8 (dir) |
- |
|
LiZnP |
5.754 |
5.765 [7] |
5.757 |
1.7 (dir) |
2.04 [7] |
|
NaMgP |
6.180 |
- |
6.376 |
1.9 (ind) |
- |
|
NaCaP |
6.713 |
- |
6.790 |
2.6 (ind) |
- |
|
NaZnP |
6.082 |
- |
6.149 |
0.8 (dir) |
- |
|
AgMgP |
5.995 |
- |
6.141 |
1.8 (dir) |
- |
|
AgCaP |
6.508 |
- |
6.478 |
1.8 (dir) |
- |
|
LiBeAs |
5.603 |
- |
5.578 [5] |
4.4 (ind) |
- |
|
LiMgAs |
6.149 |
6.180 [10] |
6.210 |
2.8 (dir) |
2.38 [8] |
|
LiCaAs |
6.719 |
- |
- |
2.6 (dir) |
- |
|
LiZnAs |
5.911 |
5.940 [6] |
5.980 |
1.6 (dir) |
1.51 [6] |
|
NaMgAs |
6.430 |
- |
6.555 [5] |
2.7 (dir) |
- |
|
NaCaAs |
6.966 |
- |
6.960 [5] |
2.2 (dir) |
- |
|
NaZnAs |
6.284 |
5.912 [10] |
6.348 [5] |
0.4 (dir) |
- |
|
AgCaAs |
6.695 |
- |
- |
1.9 (dir) |
- |
Электронная структура
Расчет энергетической зонной структуры кристаллов A1B2X5 проводился в точках высокой симметрии зоны Бриллюэна сфалерита (в ед. 2π/a): Г(0,0,0), X(0,0,0.5), L(0.5,0.5,0.5), и вдоль соответствующих направлений. Подробный расчет электронной структуры для Li-содержащих соединений был проведен нами в работе [3], где было установлено, что структура валентной зоны и зоны проводимости кристаллов A1B2X5 подобна структуре зон их бинарных аналогов - кристаллов A3X5 с решеткой сфалерита, а также было определено, что ключевую роль в формировании валентной зоны кристаллов играют анионы X.
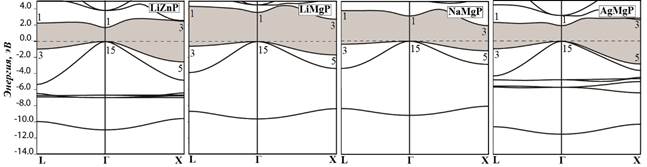
Рис. 2. Зонная структура кристаллов LiZnP, LiMgP, NaMgP, AgMgP
Характерный вид зонной структуры исследуемых кристаллов представлен на примере фосфидов (рис.2). Валентная зона LiMgP и NaMgP состоит из двух разрешенных зон, разделенных запрещенной полосой энергии порядка 5 эВ, содержащих в основном вклады s- и p-состояний атомов P. В кристалле LiZnP, в районе этой полосы расположена узкая d-зона атомов Zn. У кристалла AgMgP наблюдается более широкая дисперсия (2 эВ), в сравнении с d-зоной атомов Zn, дисперсия которой находится в пределах 1 эВ.
Установлено, что кристаллы A1B2X5 делятся на прямозонные (dir), если дно зоны проводимости и вершина валентной зоны реализуются в центре зоны Бриллюэна с симметрией Г1С и Г15V, соответственно; и непрямозонные (ind), поскольку дно зоны проводимости реализуется в точке Х, с симметрией X3C [3]. Среди фосфидов на рис.2 прямозонными являются LiZnP и AgMgP, а непрямозонными – LiMgP и NaMgP.
Вычисленные значения ширины запрещенной зоны в сравнении с экспериментальными данными представлены в таблице 1. Из 17 соединений значение запрещенной зоны для 11 кристаллов (таблица 1) приходится на область видимого спектра (от 1.8 до 3.2 эВ). Ширина запрещенной зоны кристаллов LiBeP и LiBeAs соответствует значению 4.4 эВ, что позволяет сделать вывод, что данные соединения являются диэлектриками.
Механические свойства и колебательные моды
Упругие свойства кристаллов LiBX (где B=Be, Mg, Ca, Zn; X=P, As), NaBX (где B=Mg, Ca, Zn; X=P, As), AgBX (где B=Mg, Ca; X=P, As) представляют научный и практический интерес. Это обусловлено, с одной стороны, особенностью их кристаллической структуры и химического состава, изучение которых с учетом деформационных воздействий расширяет знания о природе сил взаимодействия между атомами, входящими в состав данных соединений. С другой стороны, знание упругих свойств необходимо для подбора материалов в зависимости от сферы их применения.
В таблице 2 представлены, вычисленные нами из первых принципов упругие константы C11, C12, C44, объемные модули упругости (K), коэффициент Пуассона (ν), модуль Юнга (E), модуль сдвига (G) кристаллов A1B2X5. На основе этих параметров вычислялись коэффициент Грюнайзена (γD) и микротвердость H (ГПа). Вычисленные упругие постоянные удовлетворяют условиям механической устойчивости, которые показывают, что в нормальных условиях соединения полухейслеровского типа A1B2X5 механически устойчивы.
Коэффициент Пуассона (ν) характеризует стремление материала в процессе деформации сохранить свой объем. Если ν=0.5, материал считается несжимаемым. Среди рассматриваемых нами полухейслеровских кристаллов, наибольшее значение ν имеет AgMgP (0.35), наименьшее LiZnP (0.18).
Таблица 2
Параметры, характеризующие упругость полухейслеровских кристаллов A1B2X5
|
A1B2X5 |
C11 |
C44 |
C12 |
E |
G |
K |
ν |
K/G |
H |
γD |
υL |
υS |
ωLO |
ωTO |
||
|
LiBeP |
202 |
71 |
49 |
176 |
73 |
98 |
0,2 |
1,34 |
15 |
1,3 |
9,8 |
5,9 |
515 |
943 |
511 |
536 |
|
LiMgP |
140 |
51 |
37 |
123 |
51 |
70 |
0,21 |
1,38 |
10 |
1,3 |
8,4 |
5,1 |
379 |
707 |
376 |
412 |
|
LiCaP |
95 |
14 |
17 |
55 |
21 |
42 |
0,28 |
1,98 |
3 |
1,7 |
7,0 |
2,7 |
305 |
522 |
292 |
364 |
|
LiZnP |
132 |
58 |
35 |
127 |
54 |
66 |
0,18 |
1,23 |
11 |
1,2 |
6,0 |
4,0 |
429 |
886 |
342 |
561 |
|
NaMgP |
133 |
38 |
43 |
101 |
40 |
72 |
0,26 |
1,79 |
6 |
1,5 |
7,7 |
4,1 |
379 |
707 |
376 |
412 |
|
NaCaP |
105 |
33 |
22 |
86 |
36 |
49 |
0,2 |
1,35 |
7 |
1,3 |
7,1 |
4,0 |
331 |
587 |
329 |
379 |
|
NaZnP |
109 |
22 |
33 |
70 |
27 |
57 |
0,29 |
2,10 |
4 |
1,7 |
5,5 |
2,5 |
322 |
707 |
259 |
434 |
|
AgMgP |
118 |
39 |
77 |
80 |
30 |
89 |
0,35 |
2,97 |
3 |
2,1 |
4,8 |
2,8 |
251 |
785 |
245 |
446 |
|
AgCaP |
94 |
26 |
41 |
67 |
26 |
58 |
0,31 |
2,24 |
3 |
1,8 |
4,6 |
2,5 |
211 |
647 |
197 |
428 |
|
LiBeAs |
149 |
50 |
38 |
127 |
52 |
74 |
0,21 |
1,41 |
10 |
1,3 |
6,5 |
3,8 |
443 |
823 |
410 |
480 |
|
LiMgAs |
121 |
45 |
33 |
107 |
44 |
62 |
0,21 |
1,39 |
9 |
1,3 |
6,3 |
3,9 |
485 |
694 |
360 |
511 |
|
LiCaAs |
75 |
11 |
16 |
42 |
16 |
35 |
0,3 |
2,16 |
2 |
1,8 |
5,3 |
2,0 |
394 |
534 |
305 |
410 |
|
LiZnAs |
121 |
52 |
38 |
114 |
48 |
64 |
0,2 |
1,35 |
10 |
1,3 |
5,0 |
3,3 |
372 |
709 |
273 |
473 |
|
NaMgAs |
111 |
28 |
32 |
82 |
32 |
57 |
0,26 |
1,76 |
5 |
1,5 |
6,0 |
3,1 |
361 |
562 |
320 |
364 |
|
NaCaAs |
79 |
24 |
20 |
64 |
26 |
39 |
0,23 |
1,49 |
5 |
1,4 |
5,4 |
3,0 |
293 |
439 |
259 |
311 |
|
NaZnAs |
94 |
13 |
26 |
50 |
19 |
48 |
0,32 |
2,51 |
2 |
1,9 |
4,6 |
1,7 |
301 |
517 |
207 |
355 |
|
AgCaAs |
86 |
21 |
39 |
58 |
22 |
53 |
0,32 |
2,43 |
3 |
1,9 |
4,1 |
2,1 |
193 |
625 |
179 |
340 |
Для большинства исследуемых соединений отношение объемного модуля к модулю сдвига (K/G) меньше 1.75, что характеризует их, как хрупкие материалы. Пластичностью обладают кристаллы LiCaP, LiCaAs, NaZnP, NaZnAs, AgMgP, AgCaP и AgCaAs, у которых отношение K/G>1.90 (таблица 1).
Расчет микротвердости проводился по формуле:
![]() (2)
(2)
Вычисленные таким образом значения микротвердости полухейслеровских кристаллов A1B2X5 оказались сопоставимыми с микротвердостями их ближайших бинарных аналогов A3X5 со структурой сфалерита ZnS (2 ГПа), AlN (12 ГПа) и AlAs (5 ГПа). Расчет показал, что наиболее твердыми среди исследуемых соединений A1B2X5 являются кристаллы, содержащие атомы Li, а наиболее мягкими оказались Ag-содержащие кристаллы.
Среднее значение параметра Грюнайзена γD, для большинства металлов и простых соединений находится в интервале от 1.0 до 3.0. Для исследуемых полухейслеровских кристаллов A1B2X5 значение γD изменяется в пределах от 1.2 (LiZnP) до 2.1 (AgMgP).
В таблице 2 представлены вычисленные скорости распространения продольных (υL) и поперечных (υS) упругих волн (в км/с), а также моды продольных ωLO и поперечных ωTO оптических колебаний (в см-1), распространяющиеся в кристалле. Частоты оптических колебаний вычислены в точке Г зоны Бриллюэна и являются трехкратно вырожденными. Уменьшение скорости распространения продольных (υL) и поперечных (υS) упругих волн коррелирует с увеличением атомного номера элементов A и B в кристаллах A1B2X5.
Заключение
Выполненное теоретическое исследование в рамках теории функционала плотности позволило определить равновесные параметры решетки, упругие постоянные (C11, C12, C44), модули упругости, микротвердость, параметры Грюнайзена, скорости распространения звука (υL, υS), а также моды продольных ωLO и поперечных ωTO оптических колебаний для алмазоподобных полухейслеровских кристаллов A1B2X5 со структурой сфалерита.
Упругие постоянные полухейслеровских соединений A1B2X5 удовлетворяют условиям механической устойчивости для тетрагональных кристаллов, следовательно, изученные кристаллы при нормальных условиях будут механически устойчивыми. Установлено, что большинство материалов является хрупкими. Наиболее твердыми являются кристаллы, содержащие атомы Li и N.
Получено хорошее согласие с имеющимися экспериментальными данными. Оценка ширины запрещенной зоны Eg показала, что в группе A1B2X5 имеются перспективные кристаллы, пригодные к применению в солнечных элементах и для изготовления светодиодов, с Eg превышающей 2 эВ.
Работа выполнена в рамках госзадания Минобрнауки РФ (проект № 3.1235.2014K).
Рецензенты:
Ананьев В.А., д.х.н., доцент, профессор кафедры аналитической химии ФГБОУ ВПО «Кемеровский государственный университет», г. Кемерово;
Журавлев Ю.Н., д.ф.-м.н., профессор, первый проректор, заведующий кафедрой общей физики ФГБОУ ВПО «Кемеровский государственный университет», г. Кемерово.
Библиографическая ссылка
Басалаев Ю.М., Стародубцева М.В. СВОЙСТВА ПОЛУХЕЙСЛЕРОВСКИХ АЛМАЗОПОДОБНЫХ КРИСТАЛЛОВ СО СТРУКТУРОЙ СФАЛЕРИТА // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22329 (дата обращения: 28.02.2026).



