В настоящее время в период стремительного научно-технического прогресса возросла роль математики, а потому приобрело большую общественную значимость математическое образование. Отмечается необходимость повышения качества обучения, улучшения трудового и нравственного воспитания учащихся, укрепление связи с жизнью, улучшение подготовки школьников к общественно-полезному труду. Все эти требования особо остро стоят при обучении детей с проблемами в развитии [1, 5, 6]. Именно на уроках математики даётся определённый объём математических знаний, необходимый школьникам для успешной адаптации и интеграции в условиях современного общества [5, 6].
Математика является наиболее трудным учебным предметом для большинства учащихся с проблемами в развитии, так как требует сформированности у них таких мыслительных процессов, как отвлечение, обобщение, абстрагирование. Серьёзные трудности появляются у учеников, у которых эти процессы оказываются недостаточно развитыми [1, 5, 6]. Это касается, в первую очередь, категории школьников с нарушением интеллекта. Вместе с тем, математика и, в частности, изучение раздела «Нумерация чисел», создаёт благоприятные возможности для коррекции познавательной сферы учащихся с нарушением интеллекта.
Анализ исследований по выявлению особенностей и основных трудностей усвоения нумерации учащимися специальной (коррекционной) школы VIII вида свидетельствует о недостаточной сформированности у них понятий о числе, счёте, десятичной системе счисления (В. И. Басюра, Н. Д. Богановская, В. Ю. Неаре, В. И. Михельсон, М. Н. Перова, П. Г. Тишин, В. В. Эк и другие). В связи с чем, встаёт проблема поиска путей и педагогических условий повышения эффективности обучения математике детей с нарушением интеллекта, и конкретно, нумерации чисел.
Цель исследования
Проведенное нами исследование было направлено на совершенствование методики обучения учащихся данной категории числам четвертого концентра (нумерации чисел в пределах 1000).
Материал и методы исследования
Определяя пути и педагогические условия повышения эффективности обучения детей с нарушением интеллекта нумерации чисел в пределах 1000, мы предположили, что объяснение данной темы целесообразно осуществлять с использованием методических подходов и дидактического материала М. Монтессори («Золотой жемчужный материал», рис. 1).

Рис.1. «Золотой жемчужный материал»
Упражнения с «Золотым жемчужным материалом» позволяют сформировать у ребенка чувственные образы математических категорий в окружающем мире, создать конкретную основу для абстрактных понятий. Они помогают ему самостоятельно, через деятельность с предметами, дойти до сути математических операций и постепенно перевести их из внешнего во внутренний план. В этом смысле работа с данным материалом не самоцель, а средство закономерного перехода к математическим абстракциям [2, 4].
«Золотой жемчужный материал», как и многие другие математические материалы М. Монтессори, четко показывает связь между алгеброй и геометрией. Материал передает ребенку сведения не только о числах и действиях с ними, но также дает ясное представление о единице – как о точке, о десятке – как о линии, о сотне – как о квадрате (площади) и о тысяче – как о кубе (теле, т. е. десятке возведенной в третью степень). Работая с «Золотым жемчужным материалом», ребенок открывает для себя тождественность десяти единиц разряда и единицы непосредственно следующего за ним разряда, важную роль числа десять в десятичной системе счисления, правила выполнения арифметических действий [2, 4].
Любое натуральное число может быть представлено посредством «Золотого жемчужного материала». Отдельные бусинки («жемчужины») заменяют единицы, палочки из десяти «жемчужин» – единицы десятков, квадраты из 100 «жемчужин» – единицы сотен и кубы из 1000 «жемчужин» – единицы тысяч («Карточки с единицами разрядов», рис. 2), а суммирование заменяется механическим объединением [2, 4].

Рис.2. Карточки с единицами разрядов
Рассмотрим пример на сложение многозначных чисел без перехода через разряд. Выполняется сложение с помощью «Золотого жемчужного материала» и карточек с единицами разрядов. Ученик получает набор карт из материала «Карточки с единицами разрядов» и составляет заданные многозначные числа. Затем берёт соответствующее множество бусин из «Золотого жемчужного материала». В ходе выполнения данного задания педагог спрашивает, сколько он принёс бусин, ученик берёт каждое множество, считает вслух и распределяет по разрядам. Одновременное использование вещественной («Золотой жемчужный материал») и знаковой («Карточки с единицами разрядов») учебных моделей обеспечивает оптимальность формирования умственных действий. В форме материализации обеспечивается практическое выполнение операций (руками), что играет важную роль в обучении детей. Проделывая большое количество подобных упражнений, ребёнок постепенно переходит к тому, что начинает «предвидеть» результаты своей работы без замены раскладки «Золотого жемчужного материала», и тем самым укорачивает механический процесс.
Рассматриваемый пример иллюстрирует глубину методической проработки материалов М. Монтессори, показывает один из аспектов разрешения проблемы формализма приобретения математических знаний в рамках её педагогики [2, 3, 4].
В связи с этим, в сентябре–декабре 2014–2015 учебного года на базе ГБС(К)ОУ РМ «Саранская специальная (коррекционная) общеобразовательная школа VIII вида» г. о. Саранск с учащимися четвертого класса, нами был организован и проведён обучающий эксперимент, целью которого явилось формирование представлений о нумерации чисел в пределах 1000, их последовательности, отношениях и месте в натуральном ряду; представлений о десятичной системе счисления, арифметических действиях: сложении и вычитании.
Наша работа началась со знакомства детей с «Золотым жемчужным материалом». Занятия проводились индивидуально с каждым учеником 4 класса. Обучение проводилось поэтапно: 1 этап: введение понятий количеств (единица, десяток, сотня, тысяча); 2 этап: обучение записи чисел: 1, 10, 100, 1000 (на карточках); 3 этап: построение десятичной системы счисления; 4 этап: арифметические действия (сложение и вычитание без перехода через разряд).
Охарактеризуем работу с материалом на каждом этапе. На первом этапе ученика знакомили с количествами, представляющими разряды десятичной системы счисления, в процессе чего ребёнок обнаруживал, что единицы каждого разряда состоят из десяти единиц предыдущего разряда. Знакомство проводилось в ходе трёхступенчатого урока.
Первая ступень: Педагог кладёт перед ребёнком бусину – единицу, спрашивает, сколько здесь бусин. Ученик отвечает: «Одна». Педагог говорит: «Одна единица». Ученик ощупывает бусину. Затем педагог кладёт перед ним стержень – десяток. Спрашивает сколько бусин – единиц на стержне и т. д. Аналогично ученик устанавливает, что десять десятков составляют одну сотню, десять сотен – одну тысячу.
Вторая ступень: Педагог даёт ученику задание: «Покажи одну единицу, тысячу и т. д.». Ученик при этом ощупывает, взвешивает, перекладывает каждый из этих предметов.
Третья ступень: ребёнок сам называет указанные учителем количества.
На втором этапе знакомили детей с числами 1, 10, 100, 1000 также в ходе трёхступенчатого урока.
Первая ступень: Учитель даёт ребёнку карту с числом 1, спрашивает, какое это число. После ответа ребёнка он констатирует: «Один или одна единица». Затем он даёт ребёнку карту с числом 10 и спрашивает, какое это число. Ребёнок: «Десять». Педагог: «Десять единиц». Числа 1 и 10 уже знакомы детям. Затем педагог показывает карточку с числом 100. Спрашивает сколько нулей в этом числе. Ученик: «Два». Учитель: «Это одна сотня». Аналогично вводится понятие 1000.
Вторая ступень: Педагог даёт ребёнку задание типа: «Дай мне одну сотню, покажи тысячу, возьми один десяток» и т. д.
Третья ступень: Учитель просит ученика назвать указанные им числа.
Далее с детьми проводились упражнения по раскладке большого набора карт 1–1000 из материала «Карточки с единицами разрядов».
1. Учитель раскладывает карты на ковре в правильном порядке. В правом верхнем углу находится карта 1, под ней все карты с числами 2–10. Левее раскладываются сначала десятки, потом сотни, потом тысячи, Нужно обратить внимание на то, чтобы между картами оставалось промежуточное пространство. Отдельные карты должны выниматься так легко, чтобы не нарушить порядок остальных карт. Порядок карт ребенок знает по «Золотому материалу» из бусин. То есть, учитель берёт карты 1–9 и начинает раскладывать их одну подругой сверху вниз. При этом называет числа: «Одна единица, две единицы», а затем ребёнок продолжает работу.
2. Карты с числами одного разряда перемешивают и кладут их снова одну под другую в эту же вертикальную колонку. При этом порядок карт в колонке меняется. Начинают с карт 10–90. Учитель просит ребёнка показать названные им единицы одного и того же разряда. Аналогично поступают с разрядами сотен и тысяч. Ребёнка просят также показать числа разных разрядов, например, 20, 400, 7000 и т. д.
3. Учитель просит ребёнка назвать указанные им числа. Карты убирают так, чтобы они хранились в правильном порядке.
На третьем этапе знакомили детей с построением десятичной системы счисления, с тем, что каждый разряд содержит не более девяти единиц; сопоставление количеств и соответствующих им чисел; учили узнавать названия разрядов десятичной системы, связывать названия разрядов с определенными геометрическими фигурами, узнавать структуру десятичной системы счисления.
Для введения понятия построения десятичной системы брали поднос с 10 отдельными бусинами, 10 стержнями по 10 бусин 10 квадратами по 100 бусин, одним кубом по 1000 бусин. Введение осуществляли лишь в том случае, если ребенок уже знает множества из 10 предметов и умеет считать до 10. Учитель с ребенком приносит поднос на стол. Педагог берет одну отдельную бусину, стержень из 10 бусин, квадрат из 100 бусин и куб из 1000 бусин и кладет их перед ребенком. После чего говорит: «Одна единица, две единицы, ... Ученик продолжает. Он строит ряд из девяти бусин – единиц. Слева от единиц стержни – десятки и считает вслух: «Один десяток, два десятка, ...» Левее девять квадратов – сотен и куб – тысяча. Затем учитель говорит: «Дай мне три единицы, дай девять десятков». Педагог обращает внимание ученика на то, что ряд пуст (см. рис. 3).
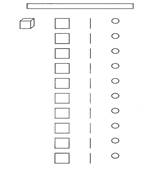
Рис. 3. Раскладка бусин
Затем работают с набором карт 1–1000. Ребёнок самостоятельно раскладывает карты тем же образом, как и в случае с большим набором карт 1–9000. После этого педагог показывает ребенку связь между количествами и числами. На одной части раскладывают «Золотой материал», а на другой – большой набор карт 1–1000. Педагог даёт ребёнку карту и просит принести столько бусин, сколько указывает число на карте. По выполнении задания бусины пересчитывают. Педагог ребёнку поочерёдно предлагает карты с числами разных разрядов.
Для закрепления изученного проводят игру. Ребёнку дают некоторое количество «Золотого жемчужного материала» и просят принести соответствующие карты. По выполнении задания бусины пересчитывают и сопоставляют с числами на картах. Учитель предлагает ребенку из представленного набора предметов из бусин (отдельных бусин, стержней, квадратов, куба) выбрать определенные множества; учитель указывает на множество, ребенок должен его назвать и заменить следующим разрядом. Учитель дает ребенку большое множество бусин одного разряда, например, 20 отдельных бусин. Ребенок отсчитывает по 10 бусин, и каждый раз заменяет их десятком. Он должен по возможности самостоятельно найти способ решения задачи. Далее работают с картами. Учитель кладет карту с числом на пустой поднос и предлагает ребенку принести соответствующее множество бусин. Сначала берется только одна карта, позже – несколько карт с числами разных категорий, например, однозначным и двузначным, двузначным и трехзначным. Учитель и ребенок вместе проверяют, соответствует ли принесенное множество заданному числу. Затем выполняется обратное задание – ребенок получает множество из бусин и приносит соответствующие карты с числами. В заключении все действия ребенок выполняет самостоятельно.
На четвертом этапе знакомили детей с процессом сложения и вычитания без перехода через разряд. Ребенку предлагается пример: 2327 + 1242= ... Числа 2327 и 1242, «записанные» с помощью карточек, и соответствующее им количество «жемчужин» выкладываются следующим образом: единицы разрядов второго слагаемого под соответствующими единицами разрядов первого. Выполняют сложение, объединяя и пересчитывая единицы поразрядно, а затем составляют полученное число (сумму) из карточек (рис. 4).
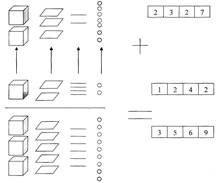
Рис. 4. Выполнение действия сложения
Таким образом, работая с материалом, ребенок самостоятельно «открывает» правило сложения многозначных чисел столбиком («поразрядность» сложения). Одновременное использование предметной («Золотой жемчужный материал») и знаковой (карточки с единицами разрядов) учебных моделей обеспечивает оптимальность формирования умственных действий. Длительная работа с конкретными материалами позволяет детям глубоко понять смысл выполнения операции сложения многозначных чисел и не только без перехода, но и с переходом через десяток.
Проделывая большое количество подобных упражнений, ребенок постепенно переходит к тому, что начинает «предвидеть» результаты своей работы без замены и раскладки «Золотого жемчужного материала», и тем самым укорачивает механический процесс. Когда он воочию «увидит» в чем дело, то сможет выполнять более трудные действия при любом количестве цифр, общепринятым способом – «в уме»; будет владеть механизмом этих действий. В действительности здесь имеет место процесс интериоризации. Предвидение результатов работы означает выполнение некоторых промежуточных действий «в уме», а значит, переход их во внутренний план [2, 4, 5].
Результаты исследования и их обсуждение
В конце учебного года был проведён сравнительный контрольный эксперимент с целью выявления степени усвоения четвероклассниками с нарушением интеллекта предлагаемого материала, а также развивающего эффекта обучения с использованием элементов Монтессори-педагогики. Необходимо было выяснить, в какой степени предложенная методика повлияла на уровень знаний учащихся пятого класса с нарушением интеллекта. С этой целью нами были обследованы дети экспериментальной и контрольной групп (контрольную группу составили учащиеся четвертого класса ГКС(К)ОУ РМ «Поводимовская специальная (коррекционная) общеобразовательная школа-интернат VIII вида»). Данные исследования свидетельствуют о весьма значительных различиях в выполнении заданий в пользу учащихся экспериментальной группы, существенными являются как качественные, так и количественные различия. Дети экспериментальной группы свободнее ориентировались в условиях заданий и успешнее выполняли их.
Заключение
Таким образом, эффективность предложенной нами методики, разработанной на основе методических подходов педагогической системы М. Монтессори, доказывают полученные результаты. Все учащиеся с нарушением интеллекта, прошедшие экспериментальное обучение, усвоили нумерацию чисел в пределах 1000, имели четкое представление о десятичной системе счисления, с легкостью выполняли арифметические действия сложения и вычитания с многозначными числами.
Рецензенты:
Мешков Н.И., д.псх.н., профессор кафедры психологии ФГБОУ ВПО «Мордовский государственный университет имени Н. П. Огарева» г. Саранск;
Исаев Е.И., д.псх.н., профессор, заведующий кафедрой педагогической психологии, педагогики и логопедии НОУ ВПО «Столичная финансово-гуманитарная академия», г. Москва.
Библиографическая ссылка
Архипова С.В., Брыжинская Г.В., Гаврилова Л.Н. ПУТИ СОВЕРШЕНСТВОВАНИЯ МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ ДЕТЕЙ С ПРОБЛЕМАМИ В РАЗВИТИИ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22274 (дата обращения: 11.02.2026).



