Для решения данной задачи построена сеточная модель фильтрации пластовой жидкости к вертикальной скважине с трещиной ГРП в цилиндрических координатах (рис. 1а).
Если трещины нет, то имеем плоскорадиальный поток к скважине. При этом давление будут постоянным на каждом круговом контуре.
Номера узлов: 0 < i < N (по радиусу) и 0 < j < M (по углу φ).
На рисунке 1б представлены ячейка с i = 5 и j = 7 и узел сетки, находящийся в центре этой ячейки i, j. А давление в этом узле равно Рi,j.
В соответствии с законом Дарси градиент давления i ÷ i-1 и j ÷ j+1 соответственно будет равен:
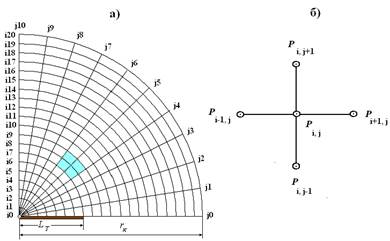
Рис. 1. Схема определения давлений в узлах сетки:
а) сектор пласта, состоящий из 200 ячеек, б) давления в ячейке
, (1)
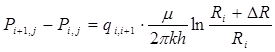, (2)
где Pi,j, Pi-1,j – давление в узлах сетки i,j и i-1,j; Ri – радиус i-го контура, м; qj+1,j, qj,j-1 – расходы жидкости вдоль контура i между ячейками i, j+1 ÷ i,j и i,j - i,j-1; μ – вязкость, Па*с; h – толщина пласта, м; k – проницаемость, м2, ∆R – шаг сетки по радиусу, м.
В этом случае перепад давления на плечах j+1 ÷ j и j ÷ j-1 рассчитывается исходя:
, (3)
, (4)
где φ — шаг по углу; qi-1,i и qi,i+1 – расходы жидкости вдоль линии i между ячейками i-1, j ÷ i,j и i,j ÷ i+1,j.
В соответствии с законом Кирхгофа для (гидравлических сетей) для каждого узла может быть записано следующее уравнение:
(Pi+1,j – Pi,j)A+ (Pj,i–Pi-1,j)B + (Pi,j–Pi,j-1)C + (Pi,j+1 – Pi,j)C = 0, (5)
где
(6)
(7)
В этом случае уравнение (5) примет более компактный вид:
K1Pi-1,j + K2 Pi,j + K3 Pi+1,j + K4 Pi,j+1 + K5 Pi,j-1 = 0, (8)
где К1 = А; К2 = - (А + В + 2С); К3 = В; К4 = К5 = С.
Как видно, получили систему уравнений из пяти неизвестных в каждом уравнении. Система уравнений (8) включает 20х10 = 200 уравнений.
Для решения этой системы уравнений граничными условиями являются:
1) в узлах (на стенке скважины) i = 0; 
давление остается постоянным Pi,j = 0;
2) в узлах (на контуре питания) i = 20; 
, давление будет в течение всего периода работы скважины постоянным и равно Рпл. В случае данного примера это давление Pi,j = 100 атм;
3) так как моделируется движение пластовой жидкости по трещине и принято, что она имеет намного большую проницаемость, чем у пласта (в 104 ÷ 105 раз), то при моделировании фильтрации принимаем давление по всей длине трещины, равное давлению в скважине, т.е.:
Р
= Рскв = 0; (9)
4) также, поскольку моделируются участки пласта, зеркальные по отношению к левой и нижней окружающей скважину зонам, то по линиям стыковки данных зон перепады давлений равняются нулю. Это означает, что перетоков жидкости нет между симметричными по распределению давления зонами, т.е.:
Р
= Р
. (10)
Аналогично записывается для границы i = 0 ÷ M и j = 10,
Р
= Р
.
Решение этих уравнений (2)–(10), записанных в конечно-разностной форме, осуществлено по методу Якоби, который заключается в том, что берутся исходные значения давлений во всех узлах сети, кроме граничных, затем ведется расчет давлений в каждом узле сетки как неизвестной величины по известным давлениям в окружающих этот узел узлах. Исходные давления при этом во всех узлах приняты равными начальному пластовому давлению. А на границах давление остается все время в соответствии с принятыми формулами (2)–(10).
Число итераций может быть задано любое, так как вычисления делаются на компьютере (для надежности принято 1000 итераций).
Поскольку пластовая жидкость поступает в скважину в основном через трещину, то дебит скважины рассчитывается как сумма дебитов между отдельными ячейками вблизи трещины, т.е. 
. А величина дебита в любой точке i равна:
(11)
Так определяем дебит скважины для всех вариантов длин трещин, рассмотренных при моделировании.
На рисунке 2 приведены результаты моделирования для Lт/Rк = 0,5, где Lт – полудлина трещины, м, Rк – радиус контура питания, м. Следовательно, длина трещины равна 125 м, что соответствует размерам достаточно протяженной трещины, получаемой при проведении массированного ГРП. Также видны распределения давления в такой системе при различных условиях фильтрации.
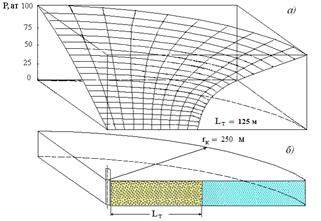
Рис. 2. Распределение давления в пласте при L/Rк = 0,5 (а)
Эти расчеты и построения позволили рассчитать дебиты скважин для различной протяженности трещин, которые являются суммами потоков. Также появляется возможность оценить отрицательный скин-фактор, соответствующий данной протяженности трещины. На рисунке 3 представлены расчетные данные об изменении продуктивности скважины после ГРП для параметра α = L/Rк. Также даются значения скин-фактора S, которые определены при условии, что до ГРП скин-фактор был равен нулю:
(12)
где ν = Qгрп / Q, α = L/Rк.
Видно, что протяженность трещины значительно влияет на показатели дебита и скин-фактора. Если радиус контура питания равен 250 м, тогда рисунок 3 можно представить в виде рисунка 4.
Формула (12) позволяет оценить отрицательный скин-фактор для различных протяженностей трещин. На рисунке 5 отражены результаты расчета скин-фактора в зависимости от полудлины трещины.
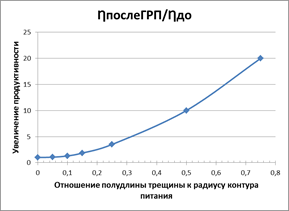
Рис. 3. Увеличение продуктивности для различных значений Lт/Rk
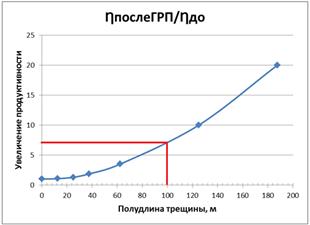
Рис. 4. Увеличение продуктивности для различных длин трещин
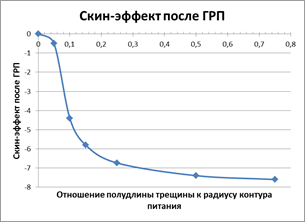
Рис. 5. Значение скин-эффекта для различных значений параметра Lт/Rk
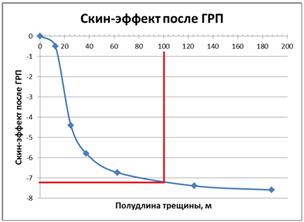
Рис. 6. Значение скин-эффекта для различной длины трещины при условии, что радиус контура питания равен 250 м
Таким образом, из представленных рисунков (4 и 6) видно, что для трещин протяженностью более 100 м, которые можно получить при проведении МГРП, продуктивность увеличивается в 7 раз и более, а скин-фактор становится отрицательным с минусовыми значениями от 7,2 до 7,6. Данные расчеты позволяют исходя из необходимого увеличения продуктивности спланировать необходимую полудлину трещин, объем закачки рабочей жидкости и проппанта. Однако стоит также отметить, что данные расчеты сделаны для условий незагрязненного пласта. На практике такие случаи встречаются крайне редко. В этой связи применять данные расчеты нельзя без точного знания величины скин-фактора до ГРП.
Рецензенты:
Грачёв С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень;
Сохошко С.К., д.т.н., заведующий кафедрой «Моделирование и управление процессами нефтегазодобычи», Институт геологии и нефтегазодобычи, ФГБОУ ТюмГНГУ, г. Тюмень.
Библиографическая ссылка
Саранча А.В., Фаик С.А., Митрофанов Д.А., Огай В.А. ОПРЕДЕЛЕНИЕ УВЕЛИЧЕНИЯ ПРОДУКТИВНОСТИ ВЕРТИКАЛЬНОЙ СКВАЖИНЫ ПОСЛЕ МГРП С ТРЕЩИНОЙ БЕСКОНЕЧНОЙ ПРОВОДИМОСТИ И НУЛЕВЫМ ЗНАЧЕНИЕМ СКИН-ЭФФЕКТА ДО ИНТЕНСИФИКАЦИИ // Современные проблемы науки и образования. – 2015. – № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22133 (дата обращения: 12.10.2024).