Разделение баскетбольных бросков на две разновидности их выполнения (без отражения и с отражением мяча от щита) было положено в 1893 году, когда установили щит, отгораживающий кольцо от зрителей, пытающихся изменить направление полёта мяча и помешать поразить кольцо команде гостей. В результате в 1903 году было официально введены щиты как часть оборудования для игры в баскетбол. Дальнейшая модификация и модернизация конструкции щита произошла за счёт частого использования щита при выполнении бросков в игре.
При бросках с отражением мяча от щита результативность зависит от правильного выбора точек прицеливания, поэтому спортсменам рекомендуется ориентироваться на дополнительный прямоугольник на щите, который является основным элементом прицеливания при бросках с отражением. Координаты точек прицеливания и отражения зависят от дистанции до кольца, параметров выпуска мяча, угла расположения спортсмена к плоскости щита, качества оборудования и инвентаря, при этом точка касания щита мячом всегда изменяется, что усложняет расчёт нахождения точек прицеливания.
Практическое определение координат точек отражения мяча от щита
Цифровые видеокамеры SONY DCR-TRV940E и SAMSYNG VP-454i, установленные на уровне кольца сбоку и сверху, фиксировали траекторию подлёта мяча к щиту, место контакта его со щитом [1]. С помощью пакета программы видеоредактора видеозапись полета мяча раскладывалась по кадрам. Выбраны «чистые» броски, когда мяч попадает в кольцо, не касаясь обода. Для нахождения координат точек отражения определяется проекция центра мяча на плоскость щита во время их контакта, и устанавливается геометрический центр отпечатка (рис. 1).
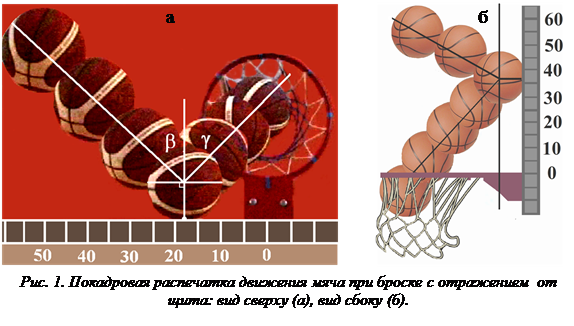
При определении координат контакта в горизонтальной проекции на поверхность площадки для результативных бросков было принято допущение о равенстве углов подлёта мяча к щиту (b) и углов отражения (g) (рис. 1а). Углы подлёта отличаются от углов отражения результативных бросков не более чем на 5° для минимальных углов расположения бросающего к плоскости щита. Данные результаты говорят о том, что для углов менее 20° происходит незначительное проскальзывание мяча по поверхности щита.
Координаты точек отражения нелинейно изменяются от центра щита к его боковой стороне при перемещении спортсмена от 90° до 10° к плоскости щита на одинаковом расстоянии до проекции центра кольца на поверхность площадки (табл. 1).
В вертикальной плоскости координаты отражения аналогично нелинейно увеличиваются при перемещении спортсмена от 90° до 10° к плоскости щита на одинаковом расстоянии до проекции центра кольца (рис. 1б, табл. 1).
Таблица 1
Координаты проекции центра мяча на плоскость щита при их взаимодействии, определённые видеосъёмкой, см
|
Угол атаки |
90° |
80° |
70° |
60° |
50° |
40° |
30° |
20° |
10° |
|
X - горизонтальная |
0 |
3 |
8 |
10 |
13 |
18 |
30 |
51 |
62 |
|
Y - вертикальная |
30 |
32 |
34 |
35 |
37 |
45 |
52 |
55 |
65 |
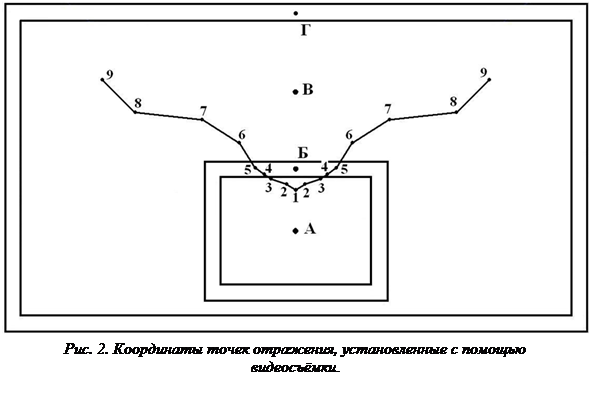
При определении вертикальных координат установлено, что координаты точек отражения меняются в зависимости от параметров траектории. Для уточнения координат отражения и параметров траектории полёта мяча проведена дополнительная видеосъёмка бросков с линии штрафного броска, в которых принимал участие мастер спорта по баскетболу. Спортсмену предлагалось выполнить серии бросков в следующие точки отражения мяча, равномерно расположенные на вертикали в центре щита: А, Б, В и Г (рис. 2).
Видеосъёмка подтвердила возможность выполнения результативных бросков с изменением вертикальных координат точек отражения в конкретном случае до ~ 70 см. Повышение высоты контакта мяча с плоскостью щита достигается изменением начальных параметров выпуска снаряда, т.е. увеличением угла и начальной скорости. Это говорит о широком диапазоне использования данных бросков при активном сопротивлении высокорослого защитника.
В результате определения точек отражения установлено:
1. Координаты точек отражения мяча от щита изменяются в зависимости от координат расположения бросающего на площадке, а именно: с уменьшением угла расположения спортсмена к плоскости щита точки отражения повышают горизонтальные и вертикальные координаты от центра к его боковой стороне.
2. В горизонтальной проекции на поверхность площадки установлено, что для результативных бросков угол подлёта к щиту примерно равен углу отражения от него.
3. Скачкообразное изменение вертикальной координаты отражения мяча от щита, например в точке 7 (рис. 2), объясняется изменением коэффициента восстановления при ударе мяча о щит в данном месте, что непосредственно связано с конструкцией каркаса исследуемого баскетбольного щита. Тыльная сторона щита крепится к каркасу, в котором имеются вертикальные ребра жесткости из прямоугольного профиля, которые приварены к габаритному каркасу щита в проекции вертикальных линий прицельного прямоугольника.
4. При ударе мяча о щит образуется отпечаток, площадь которого зависит от величины угла расположения спортсмена к плоскости щита, и размер отпечатка уменьшается при изменении угла от 90° к 10°.
Для качественного установления координат отражения необходимо провести оценку процесса удара мяча о неподвижный щит с целью определения изменения коэффициента восстановления и диапазона скоростей мяча при взаимодействии с плоскостью щита для результативных баскетбольных бросков.
Оценка процесса удара мяча о неподвижный щит
Движение тела, происходящее под действием обычных сил, характеризуется непрерывным изменением модулей и направлений скоростей его. Однако встречаются случаи, например при ударе, когда скорости точек за бесконечно малый промежуток времени (порядка 10 мс) [4] получают конечные изменения.
Удар, с точки зрения указанных положений - это явление, при котором за ничтожно малый промежуток времени скорости точек тела изменяются на конечную величину, называется ударом [7].
Так как процесс удара происходит за бесконечно малый промежуток времени, определить которое при эксперименте весьма затруднительно, воспользуемся теоремой об изменении кинетической энергии, в которую время в явной форме не входит. Данную теорему запишем для баскетбольного мяча, принимая его за математическую точку:
![]() (1)
(1)
где m – масса мяча; V0 – начальная скорость мяча; V1 – конечная скорость мяча в момент его касания о неподвижную поверхность; ΣАе – сумма работ внешних сил; ΣАi – сумма работ внутренних сил.
В начальный момент удара мяча по щиту мяч деформируется до тех пор, пока скорость его не станет равной нулю. В дальнейшем начальная кинетическая энергия мяча переходит в потенциальную энергию сил упругости деформированного мяча, а работа внутренних сил рассеивается и частично расходуется на нагревание.
Из-за остаточных деформаций и нагревания мяча первоначальная кинетическая энергия полностью не восстанавливается, поэтому мяч отделяется от поверхности со скоростью, модуль которой меньше модуля его скорости до удара.
Отношение модуля скорости мяча в конце удара к модулю его скорости в начале удара при прямом ударе мяча о неподвижную поверхность (щит) называется коэффициентом восстановления при ударе [7].
![]() (2)
(2)
где U – скорость мяча при его отскоке от щита; V – скорость мяча в момент касания со щитом.
Значения коэффициента восстановления для различных материалов соударяющихся тел определяются опытным путем. Первое сообщение об экспериментальном определении коэффициента восстановления для бросков с отражением мяча от щита было опубликовано в 2010 году [6]. Для нашего случая, когда щит можно рассматривать как абсолютно твердое тело, коэффициент восстановления полностью определяется упругими свойствами мяча. Для качественной оценки рассматриваемого процесса было проведено несколько экспериментов, результаты которых приведены в таблицах 2-4.
Таблица 2
Изменения диаметра и площади отпечатка мяча в зависимости от высоты выпуска при свободном падении мяча
|
Н, м |
0,0 |
0,1 |
0,2 |
0,5 |
1,0 |
1,5 |
1,8 |
2,0 |
3,0 |
4,0 |
5,0 |
|
d,см на щите |
2,0 |
6,3 |
8,0 |
9,8 |
11,0 |
12,0 |
12,8 |
13,0 |
14,4 |
15,0 |
16,0 |
|
Sотп, см2 |
3,1 |
31,2 |
50,3 |
75,4 |
95,1 |
113,1 |
128,7 |
132,8 |
162,9 |
176,7 |
201,1 |
Таблица 3
Изменение площади отпечатка мяча при свободном падении с высоты Н = 4 м в зависимости от угла наклона щита к горизонтальной плоскости
|
α, град |
0 |
20 |
40 |
60 |
80 |
|
S, cм² |
177 |
163 |
140 |
103 |
64 |
Таблица 4
Изменение высоты отскока мяча от баскетбольного щита в зависимости от высоты выпуска
|
Н, м |
0,255 |
0,335 |
0,455 |
0,555 |
0,655 |
0,755 |
0,855 |
0,955 |
|
h, м |
0,170 |
0,230 |
0,295 |
0,375 |
0,455 |
0,485 |
0,555 |
0,655 |
Первые два эксперимента, результаты которых приведены в таблицах 2 и 3, были проведены для определения отпечатка мяча при падении с различной высоты (табл. 2) и под различными углами падения по отношению к щиту (табл. 3). Полученные результаты показывают, что при прямом ударе диаметр отпечатка зависит нелинейно от высоты падения, т.е. dотп.= ƒ(Н). При уменьшении угла падения мяча по отношению к щиту площадь отпечатка уменьшается.
Более подробно остановимся на последнем эксперименте, полученные результаты которого представлены в таблице 4. Где Н – высота выпуска мяча, а h – высота отскока мяча.
Значение коэффициента восстановления определяется упругими свойствами мяча и может быть установлено опытным путём. При проведении эксперимента был выбран баскетбольный мяч, упругие свойства которого отвечают требованиям официальных правил баскетбола [2].
Применяя к движению мяча под действием силы тяжести теорему об изменении кинетической энергии [7], можно определить скорость мяча в момент касания его со щитом:
![]()
где g – ускорение свободного падения.
По той же теореме можно определить его скорость в момент отражения от щита:
![]()
Подставив значения V и U в формулу (2), можно определить коэффициент восстановления:
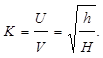
Используя приведенные формулы, можно пересчитать полученные при эксперименте данные (табл. 5) и выразить их через скорости.
Таблица 5
Изменение коэффициента восстановления при ударе мяча о щит в зависимости от скорости падения мяча
|
H, м |
V, м/с |
h, м |
U, м/c |
K |
|
0,255 |
2,24 |
0,170 |
1,83 |
0,82 |
|
0,355 |
2,64 |
0,230 |
2,12 |
0,81 |
|
0,455 |
2,99 |
0,295 |
2,40 |
0,81 |
|
0,555 |
3,30 |
0,375 |
2,71 |
0,82 |
|
0,655 |
3,58 |
0,455 |
2,99 |
0,83 |
|
0,755 |
3,85 |
0,485 |
3,08 |
0,80 |
|
0,855 |
4,09 |
0,555 |
3,30 |
0,81 |
|
0,955 |
4,33 |
0,655 |
3,58 |
0,83 |
|
1,055 |
4,55 |
0,695 |
3,69 |
0,81 |
|
1,155 |
4,76 |
0,735 |
3,80 |
0,80 |
|
1,255 |
4,96 |
0,805 |
3,97 |
0,80 |
|
1,355 |
5,15 |
0,835 |
4,05 |
0,79 |
|
1,455 |
5,34 |
0,865 |
4,12 |
0,77 |
|
1,555 |
5,52 |
0,895 |
4,19 |
0,76 |
|
1,655 |
5,70 |
0,965 |
4,35 |
0,76 |
|
1,755 |
5,86 |
1,000 |
4,43 |
0,75 |
Полученные данные показывают, что зависимость коэффициента восстановления от скорости мяча при ударе о щит носит нелинейный характер. До скорости V= 4,55 м/с коэффициент восстановления практически одинаков и равен К= 0,81 – 0,83, а затем с увеличением скорости он начинает медленно снижаться. График зависимости коэффициента восстановления от скорости мяча при ударе о щит приводится в работе [6].
Во всех случаях высота отскока h, м составляет больше 50% от высоты выпуска мяча H, м, что соответствует официальным правилам баскетбола, в которых сказано:
- Когда баскетбольный мяч ударяется о щит, он должен отскакивать от него с минимальной высотой отскока 50%.
- Баскетбольный мяч должен быть накачан до такой величины давления воздуха, чтобы при падении на игровую поверхность с высоты около 1800 мм, измеренной от нижней точки мяча, он отскакивал на высоту не менее 1200 мм и не более 1400 мм, измеренную от верхней точки мяча [2].
Подсчитанный коэффициент восстановления для данного диапазона высот при ударе мяча о поверхность площадки составляет 0,75-0,82, что соответствует диапазону изменения коэффициента восстановления при падении мяча на щит (табл. 5).
Полученные данные коэффициента восстановления при свободном падении мяча на поверхность площадки и на горизонтально расположенный баскетбольный щит, а также наличие в спортивных залах основных и дополнительных щитов, изготавливаемых из различных материалов и имеющих разнообразные конструкции каркасов и поддерживающих опор, обосновывают необходимость разработки метода определения коэффициента восстановления при ударе мяча по вертикально расположенным баскетбольным щитам.
Определение коэффициента восстановления
Коэффициент восстановления равен отношению скорости мяча после отскока (V1) к скорости удара (V0):
![]() Имеются в виду нормальные компоненты скорости мяча.
Имеются в виду нормальные компоненты скорости мяча.
Поскольку кинетическая энергия Ek пропорциональна квадрату скорости, то можно записать:
![]() Здесь также цифры 0 и 1 соответствуют значениям до удара и после удара.
Здесь также цифры 0 и 1 соответствуют значениям до удара и после удара.
Кинетическую энергию Ek можно выразить через изменение потенциальной энергии: Ek = m∙g∙H, поэтому коэффициент восстановления можно записать через значения изменений высоты подъема мяча до удара и после:
![]()
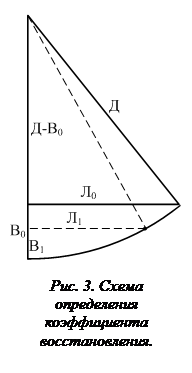
Если мяч висит на веревке длиной Д, и его отклонили в сторону на расстояние Л (как показано на рис. 3), то, исходя из теоремы Пифагора, можно записать:
![]() Отсюда изменение высоты равно:
Отсюда изменение высоты равно:![]() Теперь можно записать окончательно:
Теперь можно записать окончательно:
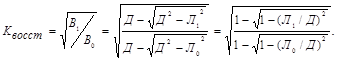 (3)
(3)
В данной формуле не учитывается эффект преобразования части кинетической энергии движения в энергию вращения мяча. Этот эффект тем меньше, чем больше длина подвеса Д.
Практическая реализация метода определения коэффициента восстановления при ударе мяча о баскетбольный щит, находящегося в рабочем состоянии, осуществляется с помощью следующего инструментария (рис. 4):

1) сборно-разборной вышки УЛТ-120М, предназначенной для строительно-монтажных, отделочных и ремонтных работ;
2) «удочки» с капроновой нитью диаметром 1,5 мм длиной от 3,07 до 3,73 м;
3) баскетбольного мяча № 7 с сеткой для транспортировки мяча.
Замеры коэффициента восстановления проводились на баскетбольных щитах (9 станций) в игровом зале санитарно-гигиенического корпуса Омского государственного медицинского университета:
- 2 основных щита (станции 1 и 4);
- 4 боковых дополнительных щита (станции 2, 3, 5, 6);
- 3 щита на передвижном бросковом модуле (станции 7, 8, 9) [3].
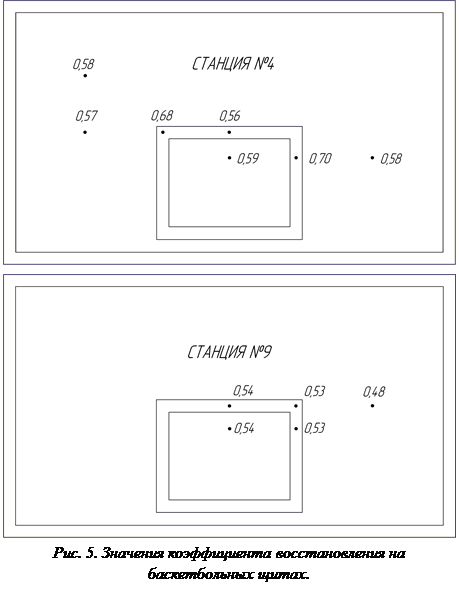
Последовательность замера коэффициента восстановления осуществлялась следующим образом. На передвижную вышку (рис. 4, поз. 1) на высоте 7,2 м от поверхности площадки закреплялась «удочка» (поз. 3) с мячом (поз. 4). Вышка подкатывалась к плоскости баскетбольного щита (поз. 5) таким образом, чтобы мяч прикасался к лицевой плоскости, а капроновая нить была параллельно плоскости. Лёгкий контакт мяча со щитом был в точке замера коэффициента восстановления. Мяч отводился на расстояние Л0, при этом капроновая нить была строго натянута (рис. 3). Затем мяч свободно отпускался. После отскока мяча, на максимальном расстоянии от щита мяч задерживался и фиксировался руками исследователя. Расстояние Л1 замерялось с помощью лазерного дальномера BoschGLМ 50. После замеров Д, Л1, Л0, по формуле (3) рассчитывался коэффициент восстановления. За счет изменения длины Д и перекатывания вышки (рис. 4, поз. 1) менялась координата на щите, в которой измерялся коэффициент восстановления. Координаты выбирались в областях взаимодействия мяча со щитом при бросках с отражением. В качестве примера на рисунке 5 представлены результаты коэффициента восстановления на основном щите (станция 4) и на сенсорном щите (станция 9) [5], который смонтирован на передвижном бросковом модуле (рис. 4, поз. 2) и используется для тестирования баскетболистов [3]. Как видно из рисунка 5, на вертикальных линиях прицельного прямоугольника коэффициент восстановления на основном щите (станция 4) выше по сравнению с другими точками этого щита, что объясняется наличием вертикальных ребер жесткости за этими линиями в каркасе баскетбольного щита. Коэффициент восстановления для сенсорного щита (рис. 4, поз. 5) ниже, чем у станции 4, так как он многослоен и демпфирует от удара мяча.
Дополнительные щиты (станции 2, 3, 5, 6) изготовлены из фанеры, которая прочно закреплена на металлических пластинах толщиной 3 мм, поэтому Квосс у них максимальный по сравнению со всеми щитами и равен 0,79. Данное значение соответствует значению Квосс при ударе мяча о пол. На передвижном бросковом модуле значение коэффициента восстановления для основного щита из оргстекла толщиной 10 мм (станция 7) составляет Квосс = 0,44, а для бокового (станция 8) Квосс = 0,50.
Предложенная схема метода и подобранный инструментарий приближают условия замеров к реальным условиям взаимодействия мяча с лицевой плоскостью щита при баскетбольных бросках с отражением.
ВЫВОДЫ
1. Коэффициент восстановления зависит от материала и конструкции щита.
2. Фактические значения коэффициента восстановления необходимы в теоретических расчётах параметров полёта баскетбольного мяча и объектов ориентирования: областей прицеливания и отражения для баскетбольных бросков с отражением мяча от щита.
3. Значение коэффициента восстановления используется для разработки методических приёмов обучения и совершенствования баскетбольных бросков с отражением мяча от щита. Например, методический приём по обоснованному выбору баскетбольных щитов с различными коэффициентами восстановления и рациональное чередование щитов при тренировке баскетбольных бросков.
4. Измерение коэффициента восстановления проводится при установке или замене баскетбольных щитов (основных, дополнительных, сенсорных) на спортсооружениях.
5. Предложенный метод определения коэффициента восстановления трудоёмок, но его использование необходимо не часто.
6. Рассматривается создание портативного прибора для определения коэффициента восстановления, который может быть использован на предприятиях, производящих баскетбольные щиты.
Рецензенты:
Кравчук А.И., д.п.н., профессор кафедры теории и методики туризма и социально-культурного сервиса, «Сибирский государственный университет физической культуры и спорта», г. Омск;
Науменко А.П., д.т.н., доцент, начальник научно-учебного центра ООО «НПЦ «Динамика», г. Омск.
Библиографическая ссылка
Притыкин В.Н., Кузнецова Н.С., Боков И.С. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ ПРИ БАСКЕТБОЛЬНЫХ БРОСКАХ С ОТРАЖЕНИЕМ МЯЧА ОТ ЩИТА // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22132 (дата обращения: 11.02.2026).



