В комплексе инженерно-строительных работ, готовым продуктом которых является завершенный объект, немаловажную часть занимают работы по созданию систем отопления, вентиляции и кондиционирования. В процессе разработки подобных комплексов, особенно с применением систем автоматизированного проектирования, часто возникает проблема грамотной формализации физических параметров текучей среды. Воздушные потоки в замкнутых объемах помещений преимущественно могут быть описаны как ламинарные и квазиламинарные (слабо возмущенные). Переход воздушных потоков в турбулентное состояние возможен при повышении числа Рейнольдса (применительно к специфике строительной отрасли – при увеличении скорости движения потока), при повышении числа Релея и Прандтля (повышение температуры газовой смеси и, как следствие, уменьшение вязкости).
Комплексы автоматизированного проектирования применительно к строительной практике (такие как ANSYS Fluent, ABAQUS CFD или CosmosFloWorks) в основе своей используют RANS-модель. В этой модели уравнения Навье-Стокса усредняются по Рейнольдсу в малом масштабе времени. Для круга строительных задач RANS-модель дает приемлемую точность результатов и, ввиду своей простоты, нашла широкое применение.
Однако при моделировании того или иного объекта инженер должен в настройках расчета указать (или уточнить) параметры турбулентного режима: масштаб и длину турбулентности. Иными словами, инженер должен указать, на сколько процентов различаются энергетические параметры потока в точках, удаленных друг от друга на длину масштаба турбулентности (далее по тексту - МТ). В противном случае задача превращается в итеративную, где критерием сходимости является требуемая температура в рабочей зоне, а функцией – МТ и/или ширина пограничного слоя вблизи отопительного прибора. Отметим, что в зависимости от геометрии системы, температурных градиентов и прочих параметров вводимые поправки будут различны от одного расчетного случая к другому. Это нашло отражение во многих трудах по теории турбулентности.
«Несмотря на значительный прогресс в подходах, основанных на решении указанной системы уравнений в рамках прямого численного моделирования… пока еще нельзя использовать их для решения задач инженерной практики. Обоснованием этого служит оценка, согласно которой для воспроизводимого спектра турбулентных вихрей отношение характерных размеров крупных и мелкомасштабных вихрей имеет порядок Re3/4. Даже на ближайшие несколько десятилетий определение всех турбулентных масштабов остается неразрешимой проблемой» [3].
Переходя к решаемой задаче, стоит рассмотреть физико-математическую модель, применяемую для расчетов. Как правило, существующие методы и модели, получившие наибольшее распространение, используют, на примере пакета CosmosFloWorks, следующий математический аппарат: уравнения сохранения массы (1), импульса (2) и энергии (3) нестационарного пространственного течения в декартовой системе координат, вращающейся с угловой скоростью Ω вокруг оси, проходящей через её начало [1; 2].
![]() (1)
(1)
![]() . (2)
. (2)
![]() . (3)
. (3)
В случае введения в расчет сжимаемых текучих сред, в дополнение к вышеперечисленным уравнениям, вводится следующее выражение, описывающие изменение плотности:
![]() . (4)
. (4)
Для учета влияния гравитации, при необходимости, вводится добавочный член:
![]() . (5)
. (5)
При проведении поверочных расчетов (моделирование классических задач докритических течений, имеющих аналитическое решение) нами была достигнута высокая сходимость расчета.
Как говорилось ранее, в процессе моделирования турбулентных течений в жилых и общественных зданиях в пакете Solid CosmoFloWorks, была обнаружена проблема описания физических процессов в пограничном слое. При достаточно точных результатах моделирования скоростей и общего характера течения газовой среды было также обнаружено явление заниженного теплообмена на поверхностях: приборы отопления имели слишком высокую температуру, а поверхности ограждающих конструкций – недостаточно высокую [7].
На предыдущих этапах изысканий данная проблема численного моделирования процессов тепломассопереноса решалась увеличением толщины пограничного слоя, увеличением шероховатости стенки и увеличением масштаба турбулентности. Пошаговое изменение величин происходило эмпирически: по достижении близких к реальным ключевых параметров (температура воздуха в рабочей зоне и на поверхности стены) изменение расчетных параметров пограничного слоя останавливалось.
Данный подход весьма трудоемок, и для каждой новой задачи необходимо проводить многокритериальную оптимизацию для достижения приемлемой точности для инженерной задачи, исходя из того что только три вышеназванных параметра доступны инженеру при решении задачи проектирования систем вентиляции и отопления.
Переходя к птицеводческим зданиям и их системам отопления, вентиляции и кондиционирования, нужно понимать, что существует большое разнообразие объемно-планировочных и технологических решений, напрямую влияющих на рассматриваемые в данной статье вопросы. В проведенном исследовании основной целью являлось уточнение численного значения МТ в совместном физическом и численном эксперименте. С этой целью была изготовлена физическая модель «помещения» (рис. 1) с соотношением сторон «высота : ширина : глубина» 1:1:1; 1:1:2 и 1:1:3. С одной из сторон модели устанавливался вентилятор – эжектор, создающий квазиламинарный поток воздуха, моделирующий распространенную схему подачи воздуха во внутренний объем птичника в условиях так называемой летней вентиляции, характеризующейся относительно высокими скоростями течения воздуха для создания охлаждающего эффекта [5; 7].
Натурная исследовательская установка состоит из внешнего корпуса, безлопастного вентилятора, анемометра Testo 416, датчиков температуры и влажности DHT22, контроллера Arduino Mega 2560. Корпус установки представляет собой куб стороной 500 мм, внутренняя поверхность которого тщательно отполирована (шероховатость не более 50 микрон). Передняя и задняя стенки в модели отсутствуют. По центру, в срезе передней грани установлен безлопастной вентилятор, позволяющий получить квазиламинарный поток воздуха.
Целью исследования являлось уточнение значений масштаба длины турбулентности потоков воздуха в отапливаемых зданиях. Определение значений масштаба длины турбулентности достигалось с помощью комбинирования натурного и численного эксперимента. При этом проводилось параметрическое численное исследование, где изменяемым параметром был масштаб длины турбулентности, а критерием сходимости – соответствие скоростей движения воздушных масс в физическом и численном эксперименте. Исходя из того, что отношение коэффициентов турбулентной диффузии и турбулентной вязкости, именуемое числом Прандтля-Шмидта, слабо меняется по самому потоку и от течения к течению, то результаты данного исследования могут быть экстраполированы на моделирование процессов тепломассопереноса в птичниках при схожих геометрических пропорциях живого сечения и температурных параметрах.

Рис. 1. Установка для исследования масштаба турбулентности
Вторым этапом эксперимента являлось создание численной модели вентилятора и модели установки. Численная модель безлопастного вентилятора учитывает все особенности внутренней и внешней геометрии, угловую скорость вращения нагнетающего вентилятора. В процессе моделирования физические свойства воздуха принимались согласно встроенным нелинейным зависимостям, приведенным на рис. 2. Надо полагать, что в пределах изменения эксплуатационных температур можно пренебречь нелинейностью физических свойств воздуха в ходе предварительных расчетов для сокращения времени расчета на ЭВМ, принимая в расчете значения для средней температуры производственного цикла в птичнике [7].
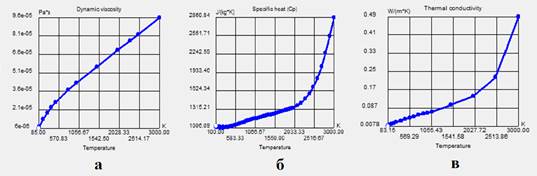
Рис. 2: а – зависимость динамической вязкости от температуры; б – зависимость теплоемкости от температуры; в – зависимость теплопроводности от температуры
На первом этапе были решены следующие задачи исследования масштаба длины турбулентности:
-
измерение скоростей истечения воздуха из безлопастного вентилятора (эжектора);
-
построение численной модели безлопастного вентилятора;
-
пересчет численной модели безлопастного вентилятора с оптимизацией масштаба длины турбулентности. В качестве критерия сходимости принимается соответствие параметров скорости истечения воздуха в численном и натурном эксперименте.
Измерение скоростей проводилось анемометром Testo 416 с диапазоном измерений от 0,4 до 40 м/с и погрешностью 0,2 м/с. Во время измерений центральное эжекционное отверстие было закрыто экраном, чтобы избежать погрешностей при измерениях. Измерения проводились в 4 точках, через 90 градусов по часовой стрелке, начиная с нижней точки сопла. Результаты измерений представлены в табл. 1
Таблица 1
Результаты натурного измерения скоростей
|
Точка 1 (0о) |
Точка 3 (180о) |
Точка 3 (180о) |
Точка 4 (270о) |
|
1,3 м/с |
1,7 м/с |
1,6 м/с |
1,4 м/с |
Таким образом, максимальная измеренная натурно скорость составила 1,7 м/с, минимальная 1,3 м/с, а средняя по сечению – 1,5 м/с [5].
Построение численной модели установки проведено в программном комплексе SolidWorks и в его CFD-приложении CosmosFlowSimulation. Принималась модель смешанного течения (ламинарное и турбулентное). Применялись уравнения Навье-Стокса, осредненные по Рейнольдсу в малом масштабе времени. Учитывалась сила гравитации. Использовалась модель реального газа (воздуха), исходные значения масштаба длины турбулентности, в которой составили 2% и 0,00054 м соответственно [5].
В модель были введены следующие допущения:
-
теплообмен в системе пренебрежимо мал;
-
не учитываются влажность воздуха и связанные с ней эффекты;
-
задача является стационарной (установившееся течение).
В качестве критерия сходимости численного эксперимента принимались следующие условия:
-
общий вид графика «параметр-итерации» (отсутствие резких скачков на конечном этапе решения показывает на устоявшееся течение) – рис. 3.
-
совпадение массовых расходов на входном и исходящем отверстии вентилятора – рис. 3.
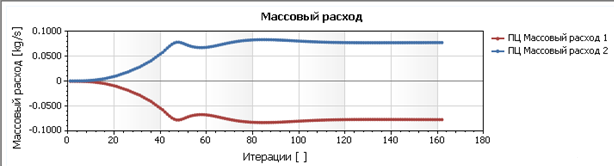
Рис. 3. Оценка сходимости расчета по расходам воздуха

Рис. 4. Распределение скоростей течения воздуха в продольном сечении модели
Невязка во входном и исходящем массовом расходе составила 0,98%, что можно считать удовлетворительной погрешностью численного эксперимента. Разница между средними по выходному сечению, результатами натурного и численного эксперимента сведена в табл. 2.
Таблица 2
Результаты натурного измерения скоростей
|
Тип эксперимента |
Скорость, м/с |
|
Натурный |
0,28 |
|
Численный |
0,31 |
Разница меж результатами составила 10,74%, что объяснимо несовершенством регистрирующей аппаратуры (большой погрешностью измерений зонда).
В качестве выводов хочется отметить, что полученные графики масштаба и интенсивности турбулентности от длины (зависимости приведены по оси симметрии, рис. 5) отображают уточненные значения физических величин, необходимых для моделирования процессов тепломассопереноса, в особенности при наличии нагонных вентиляторов, брудеров системы отопления и т.п.
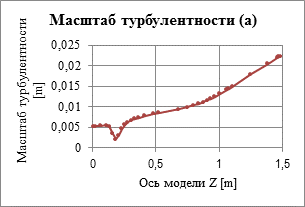
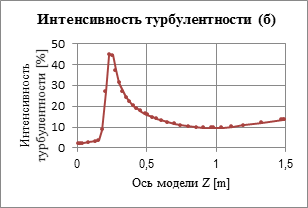
Рис. 5: а – функция масштаба турбулентности по длине модели; б – функция интенсивности турбулентности по длине модели
Что позволяет:
-
ускорить процесс расчета ввиду снижения количества итераций;
-
получить более точную картину конвективных процессов вблизи подвесного инженерного оборудования;
-
уточнить объем комфортной зоны в птичнике.
Рецензенты:
Поздеев А.Г., д.т.н., профессор, ПГТУ, ИСА, г. Йошкар-Ола;
Салихов М.Г., д.т.н., профессор, ПГТУ, ИСА, г. Йошкар-Ола.
Библиографическая ссылка
Хинканин Л.А., Хинканин А.П. ВЛИЯНИЕ МАСШТАБА ДЛИНЫ ТУРБУЛЕНТНОСТИ НА РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ВОЗДУШНЫХ ПОТОКОВ В ПТИЧНИКАХ НАПОЛЬНОГО СОДЕРЖАНИЯ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22009 (дата обращения: 28.02.2026).



