Предлагаемая работа посвящена исследованию задачи со свободными границами для нелинейного эволюционного уравнения, возникающая при математическом моделировании проблем криохирургии, когда при деструкции биологических тканей, применяются криозонды со сферическими и полусферическими аппликаторами. Для решения исследуемой задачи в работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации а также проведена конечномерная аппроксимация. В работе при 
=0 получено решение стационарной задачи, найдено приближенное решение нестационарной задачи, методом Ротэ получена аппроксимация краевой задачи в виде системы краевых задач для обыкновенных дифференциальных уравнений, с помощью функции Грина задача сведена к интегральной формулировке, для решения полученной системы интегральных уравнений применен метод нелинейных вариационных параметров. Доказана, что имеет место стабилизация решения исследуемой задачи к решению стационарной задачи за конечное время порядка 
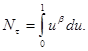Полученные результаты можно применить при конструировании и совершенствовании криоинструментов.
Эффект криогенного замораживания используется в медицине, в таких областях, как онкология, хирургия, гинекология для локального необратимого разрушения биоткани. Для этого применяются криозонды с плоской, цилиндрической или с полусферической формами охлаждающей поверхности. Работа посвящена исследованию краевой задачи со свободными границами для нелинейных эволюционных уравнений, возникающих при математическом моделировании проблем криохирургии, включая вопросы анализа и разработку конструктивных методов решения.
В работе применяются методы нелинейных интегральных, интегро-дифференциальных уравнений, метод Ротэ, метод эквивалентной линеаризации, асимптотическое интегрирование, проекционно-сеточный метод.
1. Постановка задачи.
Определение динамики температурного поля биологических тканей при деструкции тканей, когда применяются сферические и полусферические аппликаторы определяется решением следующей задачи [5,6]:
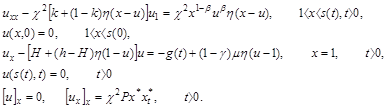(1)
В задаче (1) искомыми являются u=u(x,t), s=s(t), x*=x*(t), остальные параметры и функции известны.
Стационарная задача при =0 имеет точное аналитическое решение:
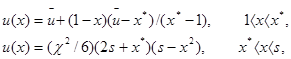(2)
где 
положительные решения нелинейной системы:
(3)
2. Интегральные уравнения задачи гипотермии.
Динамика охлаждения биоткани описывается решением следующей задачи:
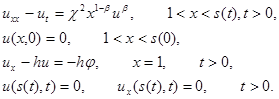(4)
Имея в виду асимптотическую устойчивость, решение задачи (4), примем u(x,t)=u(x)+v(x,t), где u(x) – решение соответствующей стационарной задачи с s(t)=s=const. Тогда для v(x,t) получаем задачу:
(5)
Рассмотрим случай 
(h>>1), тогда v(1,t)=
(t).
Решение задачи (5) будем искать в виде суммы тепловых потенциалов [3,4]:
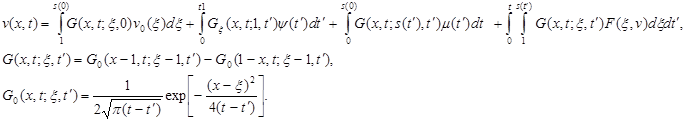(6)
Конструкция (6) удовлетворяет дифференциальному уравнению, начальному условию и краевому условию u(1,t)=(t) задачи (5) при любом выборе дифференциальной плоскости 
(t) и подлежащей определению функции s(t). Требуя, чтобы выполнялись остальные условия задачи (5) приходим к системе интегральных уравнений:
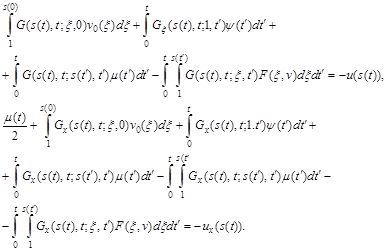(7)
Уравнения (6)-(7) образуют замкнутую систему нелинейных интегральных уравнений относительно v(x,t), (t) и s(t).
Определение пары u=u(x) и s требует решения соответствующего (4) стационарной задачи со свободной границей для уравнения типа Эмдена-Фаулера.
С помощью функции Грина определение пары u=u(x) и s сводится к решению нелинейного интегрального уравнения Вольтера 
и нелинейного уравнения 
. При =0, получаем: 
где s-положительный корень уравнения 
который определяется по формулам Кардана. Из условия u(1)
1 вытекает условие 
.
При 0<1 приближенное решение будем искать в виде: 
где А, s, b, - неизвестные постоянные параметры. Потребуем, чтобы выполнялась асимптотика, которая вытекает из дифференциального уравнения при x
s так что 
, и краевое условие при х=1, что приводит к следующим выражениям: 
, где y=s-1 положительный корень уравнения: 
.
При 
, (7) принимает вид:
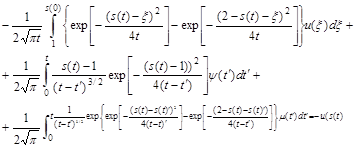(8) 
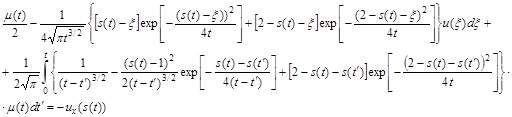(9)
Определив из нее функции 
и s=s(t), c помощью квадратуры, находим v(x,t), 1<x<s(t), t>0.
Полагая t=T, Т
первое из уравнений системы обращается в тождество, а второе трансформируется к виду: 
.
Так как 
, то ядро интегрального уравнения интегрируема, и, следовательно, 
=0. Согласно квадратуре, V(x,T) 
, и поэтому u(x,T) 
, при Т.
Используя метод Ротэ, для задачи (4) получаем следующую аппроксимацию задачи [1,2]:
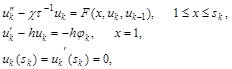(10)
где 
С помощью функции Грина, решение дифференциального уравнения (10) имеет вид:
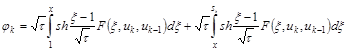. (11)
После преобразований получаем:
, 
, (12)
где индекс k – опущен, а знак «v» означает значение на k-1 временном слое, 
.
Потребуем, чтобы (12) удовлетворяло краевому условию при x=1 задачи (10). Это приводит к дополнительному нелинейному уравнению:
. (13)
Таким образом, задача (10) сведена к нелинейному интегральному уравнению (12) типа Вольтера и уравнению (13).
Конечномерная аппроксимация (12), (13) приводит к системе нелинейных алгебраических уравнений относительно узловых значений 
и числа k.
Простейшие приближенные решения для (12), (13) можно искать в виде:
1<x<s. (14)
Для u и s при этом получаем систему нелинейных уравнений, удовлетворяющее условию
. Оно содержит подлежащие определению величины 
и 
.
Приближенное решение задачи будем искать в виде:
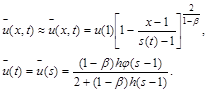(15)
Краевые условия при этом выполняются автоматически для любой функции s=s(t). Предположим, что конструкция (15) удовлетворяет дифференциальному уравнению в смысле равенства нулю интегральной невязки. В результате приходим к задаче Коши для определения s(t). Заменим du/dt конечно-разностной схемой, получаем нелинейные уравнения для определения s на данном временном слое.
3. Пространственная локализация и стабилизация за конечное время.
Для первого шага (к=1) из (12), (13) имеем:
,
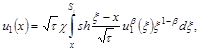
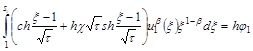. (16)
При h=
и для определения 
получаем уравнение
, (17)
и формулу для последующего определения 
:
, . (18)
На k-м шаге для получаем такое же уравнение:
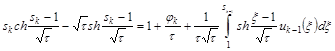(19)
и квадратуру для последующего определения 
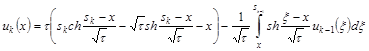. (20)
Уравнение (20) отличается от (17) только правой частью. Поэтому достаточно рассмотреть вопрос о разрешимости уравнения типа 
, где 
Такое уравнение имеет единственное решение, если функция f(x) монотонно возрастающая. Нетрудно видеть, что f(1)=1, а 
для всех x>1, 
<1. Следовательно, уравнение (17) и все последующие уравнения (20) однозначно разрешимы, причем 
таким образом, на каждом временном шаге краевая задача имеет финитное решение [2,3].
По физическому смыслу 
с увеличением к, s определяется из соответствующей стационарной задачи. Решение этой задачи можно получить формально переходя к пределу при 
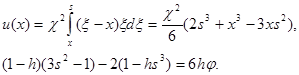(21)
Из общих теорем [1] следует, что для всех имеет место стабилизация решения задачи (1) к решению стационарной задачи за конечное время порядка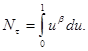
Алгоритмы получения приближенных решений реализованы на ЭВМ. Результаты численных расчетов сведены в таблицу:
|
|
|||
|
|
1 |
1 |
2 |
|
|
2 |
3 |
2 |
|
|
1.05 |
1.20 |
1.08 |
|
|
2.14 |
2.32 |
1.68 |
Рецензенты:
Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского научного центра РАН, г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного геофизического института, г. Нальчик;
Пен Р.З., д.т.н., профессор, профессор кафедры машин и аппаратов промышленных технологий ФГБОУ ВО Сибирский государственный технологический университет, г. Красноярск.
Библиографическая ссылка
Кайгермазов А.А., Кудаева Ф.Х. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СФЕРИЧЕСКИ-СИММЕТРИЧНОЙ ГИПОТЕРМИИ БИОТКАНИ // Современные проблемы науки и образования. – 2015. – № 2-2. ;URL: https://science-education.ru/ru/article/view?id=22001 (дата обращения: 08.12.2024).