Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ларин А.Г. 1 Москвичева Ю.А. 1

---

1 Нижегородский государственный технический университет им. Р.Е. Алексеева

Рассматривается движение ледокольной платформы с малой скоростью над ледяным покровом. Модель ледяного поля – тонкая изотропная однородная пластина постоянной толщины, лежащая на упругом основании гидравлического типа. Определяется напряженно-деформированное состояние бесконечной, полубесконечной пластины и полубесконечной пластины, имеющей вырез в форме ледового канала. Нагрузка от платформы считается равномерно распределенной по площади прямоугольника с варьируемым отношением длины к ширине. Исследуется влияние величины давления, формы и площади нагрузки на напряженно-деформированное состояние. Даются рекомендации по проектированию платформ.

Статья в формате PDF

282 KB

ледяной покров

напряженно-деформированное состояние

изгиб

ледокольная платформа на воздушной подушке

1. Голушкевич С.С. О некоторых задачах изгиба ледяного покрова. Л.: Воениздат, 1947. – 331 с.

2. Зуев В.А. Средства продления навигации на внутренних водных путях. Судостроение. Л.: 1986 – 208 с.

3. Зуев В.А., Грамузов Е.М., Двойченко Ю.А. Разрушение ледяного покрова. НТО им. Акад. А.Н. Крылова. В-кмежобл.правл. матер. По обмену опытом, вып. №2. Горький, 1989.

4. Лавров В.В. Деформация и прочность льда. Гидрометиздат. Л.: 1969

5. Мавлютин Р.Р. Концентрация напряжений в элементах авиационных конструкций. М.: Наука. 1981 – 141 с.

6. Справочник по строительной механике корабля под ред. Ю.А. Шиманского. Т.2. – Л.: Судостроение 1982 – 164 с.

Еще в конце прошлого века был обнаружен значительный эффект разрушения ледяного покрова и прокладки судоходного канала при движении платформы на воздушной подушке (ЛПВП) [2]. Экспериментально было замечено, что если напор воздуха в воздушной подушке (ВП) превышает толщину льда, то через щели и трещины, или через кромку разрушенного льда воздух поступает под ледяной покров и образует под ним воздушную полость. В этом случае вода (упругое основание гидравлического типа) перестает поддерживать ледяной покров, который находится только под действием сил собственной тяжести и упругости.

При вполне определенных размерах ВП в плане, зависящих от толщины льда и его физикомеханических характеристик, ледяной покров начинает самопроизвольно разрушаться. В этом случае энергетические затраты на разрушение льда не велики по сравнению с результатами по известным ледокольным средствам [2] и связаны только с энергией на образование ВП. Возможен и другой случай, когда воздушная полость не заходит под ледяной покров, но лед может разрушаться при значительном давлении в ВП [2], хотя эффект при этом несколько снижается.

В настоящей статье ставится задача оценить напряженно-деформированное состояние (НДС) ледяного покрова при разных схемах взаимодействия СВП со льдом, а также влиянием отношения длины и ширины ВП. Результаты решения могут использоваться при оптимизации проектных характеристик ЛПВП.

При разрушении ледяного покрова ЛПВП характеризуются значительными давлениями в ВП (до 10 кПа) и относительно низкими скоростями движения (до 12 км/час).

Взаимодействие ЛПВП с ледяным покровом будем полагать квазистатическим. Под разрушением ледяного покрова будем понимать возникновение таких напряжений от его изгиба, при которых появляются магистральные трещины (предвозвестники полного пролома льда).

В качестве расчетной схемы приняты случаи нагружения бесконечной и полубесконечной ледовой пластины с равномерной распределенной нагрузкой по форме квадрата и прямоугольника, а также бесконечной пластины с вырезом в плане в форме ледового канала. Эти схемы соответствуют реальным при движении ЛПВП в сплошном льду (рис. 1).

Рис. 1. Схемы взаимодействия ЛПВП со льдом

а) нагрузка на площади квадрата в бесконечной пластине;б) нагрузка в форме прямоугольника в бесконечной пластине;в) нагрузка в форме прямоугольника на полубесконечной пластине;г) нагрузка в форме прямоугольника в пластине с вырезом

Рассмотрим наименее благоприятную схему, когда подо льдом не образуется воздушная полость. Ледяной покров считаем тонкой однородной изотропной упругой пластиной на упругом основании гидравлического типа.

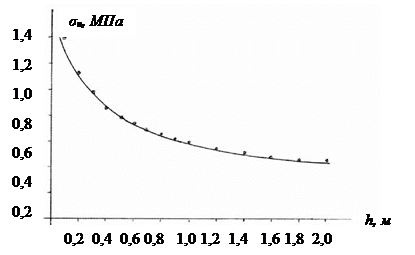
Расчет НДС ледяной пластины проводим методом конечных элементов в пакете COSMOSM. В качестве расчетных характеристик материала приняты: модуль упругости Е = 5000 Мпа, коэффициент Пуассона μ = 0,34. Предел прочности льда на изгиб принят по рекомендациям В.В. Лаврова [4], где приведен график σн = f(k) при отрицательных температурах воздуха. Этот график с достаточной точностью можно аппроксимировать зависимостью

Рис. 2. Зависимость σ = f(h) по В.В. Лаврову [4]_________ и аппроксимация • • • • •

При решении задач численным методом бесконечная пластина заменялась пластиной конечных размеров. В качестве критерия удаления внешних кромок выбрано равенство приложенного усилия суммарному отпору упругого основания. При удалении границ от места приложения нагрузки на 6 характерных длин изгиба пластиныr, ее можно считать бесконечной, с погрешностью, не превышающей 1%.

В зависимости (2):

Е, μ – модуль упругости и коэффициент Пуассона для льда;

h – толщина льда;

ρв – плотность воды;

g – ускорение свободного падения

Для выбора размеров конечного элемента был выполнен расчет для разных его размеров и проведено сравнение с аналитическим решением. Элементы разных размеров Δ «бесконечной» пластины нагружались равным по величине суммарным усилием Q и полученный прогиб под ним сравнивался с прогибом от сосредоточенной силы P той же величины, вычисленным по формуле Герца [6] для бесконечной пластины в начале координат.

Где D – цилиндрическая жесткость пластины при изгибе,

Схема нагружения показана на рис. 3

Рис. 3. Расчетная схема при определении размера элемента

При относительном размере элемента решение Герца и численное решение по предложенной методике, относительная погрешность не превышает 0,5%.

Бесконечная пластина, нагруженная равномерной нагрузкой в форме квадрата

Нагрузка равномерно распределена в форме квадрата со стороной а. Относительный размер нагрузки a/r варьировался от 0,1 до 3,5 с шагом 0,1 и от 3,5 до 5,0 с шагом 0,5. Изгибные напряжения принимались по рис. 2. В качестве расчетного принято давление равное Р = ρgh, Па (при h = 0,1 м). Безразмерные величины определялись по формулам:

где W – прогиб пластины.

График безразмерных напряжений   в ледяной пластине при постоянном давлении приведен на рис.4

Как видно из рис. 4, максимальные напряжения в рассмотренном случае возникают при безразмерной стороне квадрата a/r = 3 ÷ 3,5.

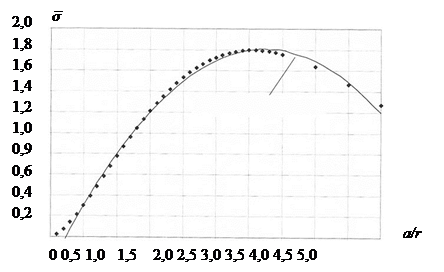
Рис. 4. График безразмерных напряжений в ледяной пластине при постоянном давлении, распределенном по площади квадрата со стороной а

Напряжения для пластины могут быть вычислены с помощью формул [6]

Изгибающий момент от сосредоточенной силы в цилиндрических координатах можно определить [6]

где:– постоянная Эйлера ();

R – текущий радиус;

P – сосредоточенное усилие;

– радиальный и тангенциальный моменты.

Подставив (6) в (5) можно видеть, что связь между напряжением и нагрузкой носит линейный характер для заданной толщины льда, формы и площади нагрузки.

Для других толщин льда давление, приводящее к образованию трещин при заданной площади и отношении сторон можно получить простым пересчетом.

Бесконечная пластина, нагруженная равномерной нагрузкой в форме прямоугольника

Нагрузка распределена в форме прямоугольника со сторонами а и в. Отношение сторон нагрузки а/в варьируется от 0,5 до 2,0 с шагом 0,1 и от 2,5 до 4,0 с шагом 0,5. Относительная площадь варьируется от 0,5 до 1,5 с шагом 0,25 и от 2,0 до 4,0 с шагом 0,5.

В качестве расчетной принята нагрузка . Результаты расчета приведены на рис.5.

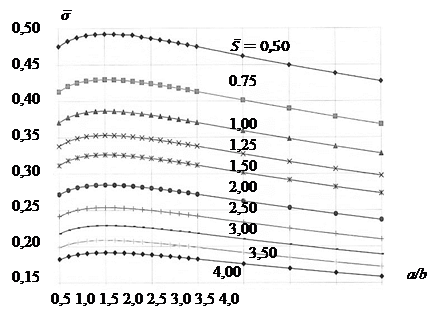
Рис. 5. Безразмерные напряжения в бесконечной пластине при постоянной нагрузке, распределенной по площади прямоугольника

Полубесконечная пластина, нагруженная равномерной нагрузкой в форме прямоугольника

Расчетные параметры нагрузки приняты как в предыдущем случае. График безразмерных напряжений в полубесконечной пластине при постоянной нагрузке, распределенной по площади прямоугольника, приведены на рис.6.

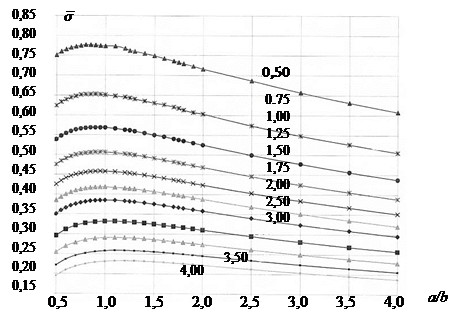
Рис. 6. График безразмерных напряжений в полубесконечной ледяной пластине при постоянной нагрузке, распределенной по площади прямоугольника со сторонами а и в

Анализ полученных данных показывает, что при относительно небольших площадях (до ) напряжения, вызываемые одинаковой по величине суммарной нагрузкой в 1,5 раза больше для полубесконечной пластины, чем для бесконечной. По мере роста площади нагрузки это отношение уменьшается.

Полубесконечная пластина с вырезом в форме канала

Нагрузка распределена в форме прямоугольника со сторонами а и в. Отношение сторон нагрузки варьировалось от 0,5 до 2,0 с шагом 0,1 и от 2,5 до 4,0 с шагом 0,5. Относительная ширина канала варьировалась от 1,0 до 4,0 с шагом 1,0. Расчетной принята нагрузка h=0,1 м.

Отношение напряжений в «полубесконечной» пластине с вырезом при постоянной нагрузке приведены в табл. 1

Таблица 1

Отношение напряжений в «полубесконечной» пластине с вырезом при постоянной суммарной нагрузке

При расчете движения в канале необходимо учитывать концентрацию напряжений в углах вырезов. Как отмечается в [5], для учета концентрации напряжений в углах вырезов необходимо выбирать меньшие размеры конечных элементов, что и было сделано. По мере уменьшения размеров элементов, величина напряжений в районах концентрации растет.

Сравнивая данные расчетов для полубесконечной пластины с вырезом в форме канала и без него, можно видеть, что напряжения на оси симметрии для одинаковых относительных площадей и отношений а/в при равной суммарной нагрузке оказываются близки. Трещины из-за повышения напряжений будут образовываться в углах выреза.

Следовательно, для расчетного случая при определении НДС следует выбирать нагружение полубесконечной пластины, т.к. он требует больших усилий.

Оптимальное соотношение сторон нагрузки при проектировании ЛПВП целесообразно принимать равным 1.

Рецензенты:

Зуев В.А., д.т.н., профессор, заведующий кафедрой кораблестроения и авиационной техники Нижегородского государственного технического университета им. Р.Е. Алексеева, г. Нижний Новгород;

Грамузов Е.М., д.т.н., профессор кафедры кораблестроения и авиационной техники Нижегородского государственного технического университета им. Р.Е. Алексеева, г. Нижний Новгород.

Библиографическая ссылка