Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Димитриев А.П. 1

---

1 ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»

Задача составления расписания учебных занятий имеет много решений. При поиске лучших решений возникает вопрос о том, когда следует остановить поиск. Исследовано несколько критериев остановки процесса, в основе которых: длительное отсутствие улучшения значения целевой функции; факт, что специфический график, создающий представление о дисперсии, примерно на одном уровне; отсутствие лучших значений в окрестности достигнутой точки. Приводятся графики, которые иллюстрируют применение второго критерия. Показано, что наибольшей значимостью обладает третий из критериев. Разработана компьютерная программа в свободно распространяемой системе программирования Turbo Delphi 2006, реализующая использование различных критериев прекращения поиска для различных алгоритмов. В качестве исходных данных для этой программы использованы в том числе ранее опубликованные наборы данных. Программа использует несколько параметров, корректируемых пользователем. Результаты экспериментов сведены в таблицы.

Статья в формате PDF

153 KB

оптимизация

расписание

целевая функция

алгоритм

1. Димитриев А.П. Модели и алгоритмы в системах автоматизированного перевода текста // Прикладная информатика. – 2013. – № 6 (48). – С.45-59.

2. Димитриев А.П. Модификация алгоритма оптимизации последовательности отбора для решения задачи коммивояжёра // Современные проблемы науки и образования. – 2015. – № 2. – С. 184.

3. Димитриев А.П., Романова Т.Ю. Моделирование составления расписания учебных занятий методом PSO на сетях Петри // Динамика нелинейных дискретных электротехнических и электронных систем : материалы 11-й Всерос. науч.-техн. конф. – Чебоксары : Изд-во Чуваш. ун-та, 2015. – С. 396-397.

4. Желтов В.П., Димитриев А.П. Стохастическая оптимизация расписания на сетях Петри. – Чебоксары : Изд-во Чуваш. ун-та, 2001. – 213 с.

5. Carling K., Meng X. On statistical bounds of heuristic solutions to location problems // J. of Global Optimization. – 2015. - 32 p. - URL: http://link.springer.com/content/pdf/10.1007%2Fs10878-015-9839-0.pdf (accessed 02.09.2015).

6. Hamming distance // Federal Standard 1037 C. - 1996. - URL: http://www.its.bldrdoc.gov/fs-1037/fs-1037c.htm (accessed 02.09.2015).

7. Kearfott R.B. On rigorous upper bounds to a global optimum // J. of Global Optimization. – 2014. – № 59. – P. 459-476. - URL: http://interval.louisiana.edu/preprints/2012-perturb-to-feasibility.pdf (accessed 02.09.2015).

8. Kryzhanovsky B.V., Kryzhanovsky V.M. The shape of a local minimum and the probability of its detection in random search // Lecture Notes in Electrical Engineering. – 2009. – Vol. 24. – P. 51 61.

Составление расписания учебных занятий в вузе является актуальной задачей. Как и в любом планировании, здесь имеются критерии планирования, на основании которых в [4] разработан критерий качества расписания. Он выражается положительным числом C.

Задача обычно имеет много решений, из которых целесообразно выбрать по возможности лучшее в соответствии со значением C. Нахождение каждого из вариантов решения данной задачи занимает некоторое время. Даже если автоматизировать процесс, рассмотрение всех вариантов практически невозможно. При анализе решений возникает вопрос о том, когда следует остановиться и принять в качестве результата наилучший из найденных вариантов. Назовем это моментом остановки.

Цель работы – выработка обоснованного критерия остановки вычислительного процесса при дискретной оптимизации, связанной с составлением расписания.

В качестве такого критерия часто выбирается достижение заданного числа итераций [5], причем авторы [5] взамен достижения такого числа предлагают использовать статистические методы. Иногда применяется условие достижения некоторой границы, при этом в [7] предлагается альтернативный метод, основанный на использовании градиента. Однако применение градиента характерно в основном для непрерывной оптимизации, а не дискретной, как в случае расписания.

Авторы работы [8] представляют вероятность нахождения локального минимума как функцию «глубины» минимума. Опираясь на ряд уже найденных минимумов, они оценивают вероятность нахождения более «глубокого» минимума и принимают решение за или против дальнейшей работы программы.

Область исследования

Предлагается несколько критериев возможности остановки вычислительного процесса:

– если при оптимизации не происходит улучшения значения C;

– если график вторых сумм по интервалам времени на периоде, формирующий представление о дисперсии этих сумм, остается примерно на одном уровне, т.е. если дисперсия близка к нулю;

– если в окрестности достигнутой точки нет лучших значений C.

Каждый из критериев требует исследования, для чего используем имитационную модель [1]. Она имеет несколько областей практической реализации, в том числе составление расписания учебных занятий. Модель универсальна для ряда задач дискретной оптимизации. Задача составления расписания в [1] представлена как задача нахождения минимума целевой функции:

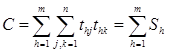, (1)

где n – число объектов, каждый из которых представляет совокупность учебных занятий соответствующей академической группы; th, j – значение j-го объекта в h-й интервал времени (учебную пару). Здесь Sh характеризует слагаемое целевой функции в h-й интервал времени. От начального интервала времени j-го объекта и до интервала времени, определяемого его параметром pj (числом занятий для группы), значение объекта равно количеству студентов для объекта tj, а в остальное время оно нулевое. Интервалы времени разделяют период времени, для которого составляется расписание (учебную неделю), на равные отрезки; всего m интервалов.

Для работы с данной моделью в [1] предложен наиболее эффективный из всех известных алгоритмов решения задачи, который будем называть алгоритмом отбора. Его суть в оптимизации последовательности отбора входных данных методом имитации отжига для поочередного размещения в оптимальных в области допустимых значений для данного объекта интервалах времени. Как альтернатива алгоритму в [1] применен муравьиный алгоритм вместо имитации отжига, но он приводил к значительно худшим результатам (C=2878682), что даже хуже, чем результаты не лучших алгоритмов, предложенных в [1] (C=2877487).

Для файла f1 [1; 2] за 20 мин работы на одном процессоре современного персонального компьютера при использовании алгоритма отбора получено минимальное значение C=2877250. Прочие алгоритмы его не достигают. Это значение и свойства полученного расписания далее используются для сравнения критериев.

Рассмотрим предлагаемые критерии.

Длительное отсутствие улучшения

Здесь имеется некоторое сходство с критерием задания числа итераций, о котором сообщалось во введении, но в действительности это число задается динамически каждый раз при улучшении C. С целью исследования данного метода разработана компьютерная программа в свободно распространяемой системе программирования Turbo Delphi 2006, реализующая использование различных критериев прекращения поиска для различных алгоритмов. Программа использует несколько параметров, корректируемых пользователем. Длительное отсутствие улучшения наблюдается для разных алгоритмов. Например, алгоритм покоординатного спуска здесь значительно менее эффективен (типичные значения C для f1 составляют 2921070), и он не приведет к лучшим значениям, даже если будет долго работать. В дополнение к рассмотренным в [1] алгоритмам исследовано применение метода «роя частиц» [3]. Так, при 900 частицах и 1 миллионе итераций изменения значений скоростей частиц (что длительно) варьировались параметры метода, использован файл исходных данных f1. У алгоритма три стандартных параметра:

– множитель скорости;

– множитель для слагаемого, представляющего разницу C между наилучшим и текущим положениями частицы;

– множитель для слагаемого, представляющего разницу C между наилучшим положением роя и текущим положением частицы. Результаты исследования методом «роя частиц» сведены в табл. 1.

Таблица 1

Значения C, полученные при различных параметрах метода «роя частиц»

Из табл. 1 следует, что метод «роя частиц» также оставляет желать много лучшего по сравнению с алгоритмом отбора. Возможно, допустимы (однако еще не открыты) алгоритмы, находящие значения C, лучшие, чем находит алгоритм отбора, поэтому даже если длительное время использовать данный алгоритм, существует вероятность обнаружения лучших вариантов значений C.

Таким образом, данный критерий достижения оптимума следует рассматривать относительно используемого алгоритма. Он не является абсолютным.

График, дающий представление о дисперсии Sh для всех интервалов периода

О том, как график, дающий представление о дисперсии величины Sh (рис. 1), связан с C, отмечено в [1]. Данный график новый и построен при минимальном из когда-либо достигнутых значений C. На каждом интервале времени график проходит почти на одном уровне, т.е. дисперсия величины, отложенной по оси ординат, близка к нулю, однако нулю она не равна.

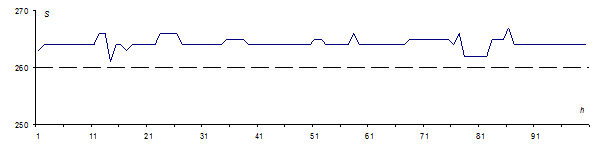
Рис. 1. График зависимости S(h),

дающий представление о дисперсии величины Sh для f1 при C=2877250.

Так как в файле f1 много объектов и получить абсолютно минимальное значение полным перебором вариантов невозможно, рассмотрим файл исходных данных f7 (табл. 2). В нем меньше и объектов, и интервалов времени: n=10, m=25.

Таблица 2

Данные файла f7 и результат оптимизации

Для решения задачи применен алгоритм отбора при следующих параметрах [1]:

– начальное число итераций – 1000;

– увеличение числа итераций при изменении температуры – 250;

– количество изменений температуры – 10;

– обмен трех объектов на расстоянии до восьми единиц (в последовательности).

Используя параметры, приведенные в табл. 2 (а также при некоторых других комбинациях параметров), за 40 с на современном компьютере получено значение C=185852. Метод покоординатного спуска из случайной точки приводил к значению 187212, а алгоритм с номером 2 [1] – к значению 186649, т.е. использованный алгоритм отбора правильно выбран как более эффективный.

C уменьшением числа объектов отклонения от среднего по сравнению с f1 (рис. 1) стали значительно больше (рис. 2). В то же время существенных качественных изменений по сравнению с размещением при значении C, равном 187212, не произошло. График второго ряда только незначительно больше отклоняется от среднего значения, чем график первого ряда. На графике для C=188966 (рис. 3), полученного генетическим алгоритмом Genitor, дисперсия больше предыдущей (нижняя точка графика почти касается ординаты со значением 100), т.е. даже при не очень значительном улучшении C происходит уменьшение дисперсии.

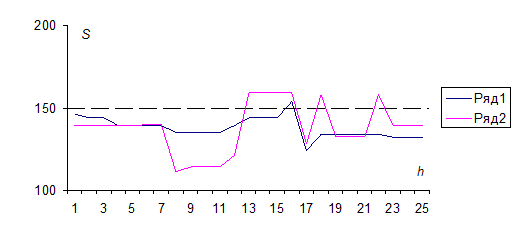
Рис. 2. График зависимости S(h), дающий представление о дисперсии величины Sh для f7:

– ряд 1 соответствует графику при C=185852;

– ряд 2 соответствует графику при C=187212.

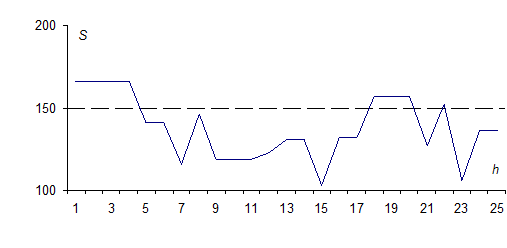
Рис. 3. График зависимости S(h),

дающий представление о дисперсии величины Sh для f7 при C=188966.

Однако нулевой дисперсия не становится. Кроме того, такой график можно построить только для некоторого класса задач. Таким образом, приблизительная «линейность» рассматриваемого графика не может считаться критерием остановки, так как она не всегда достижима, однако некоторая связь здесь присутствует.

Исследование окрестности достигнутой точки

Следующий критерий основан на исследовании окрестности достигнутой точки на наличие лучших значений C. Для этого производится полный перебор всевозможных перемещений каждой пары объектов. Тут имеется некое подобие хэммингова расстояния [6] между лучшими значениями. При использовании расстояния Хэмминга строки длины n означают результаты оптимизации (см., например, строку «Начальный интервал» табл. 2), а алфавит состоит из m символов. Для файла f1 и C=2877250 такое расстояние больше двух, так как надо одновременно изменить значения по крайней мере трех координат (начал объектов), чтобы найти лучшее значение С. Выяснение того, что меньших значений в окрестности нет, заняло около 2,5 мин машинного времени Это локальный экстремум, однако, пока не найдено меньших значений C, имеется вероятность, что он глобальный.

В то же время, начиная из точки локального экстремума со значением C, равным 2877387, методом исследования окрестности найдены лучшие значения: сначала 2877385, а затем 2877384. Это показывает, что у локального экстремума по соседству имелся лучший локальный экстремум, и следовательно, логичность метода проверки подтверждена.

Заключение

Выбору момента остановки из приведенных критериев наиболее полно удовлетворяет третий критерий, основанный на исследовании окрестности достигнутой точки. Тем не менее его применение занимает существенное машинное время.

Интерпретируя результаты исследования алгоритмов по составлению реальных расписаний учебных занятий, следует заметить, что изменения должны касаться расположения учебных занятий как в сетке часов, так и в аудиториях. Если не удается улучшить расписание перемещением только одного занятия, может потребоваться одновременное перемещение двух и более занятий.

Рецензенты:

Славутский Л.А., д.ф.-м.н., профессор кафедры автоматики и управления в технических системах ФГБОУ ВПО «ЧГУ им. И.Н. Ульянова», г. Чебоксары;

Пряников В.С., д.т.н., профессор кафедры радиотехники и радиотехнических систем ФГБОУ ВПО «ЧГУ им. И.Н. Ульянова», г. Чебоксары.

Библиографическая ссылка