Проблемы математического моделирования продуктивности сельскохозяйственных земель связаны с необходимостью учета значительного числа параметров различной физической природы, включая такие группы, как почвенные (тип, химический состав, структура, гидрология), климатические (тепло- и влаго обеспеченность, ветровая нагрузка), мелиоративное состояние (гумусовый слой, плотность сложения, засоленность), экологические и др. [2].
Для устранения описанной проблемы «проклятия размерности», присущей моделированию продуктивности сельскохозяйственных земель, предлагается использовать нечеткое множественное моделирование [4, 5], которое более эффективно, в случаях, когда существует недостаточность или неопределенность информации об исследуемой антропогенной системе; значительная часть информации получена на основе экспертных данных или эмпирических описаний процессов; параметры и входные данные не являются точными и корректно сформулированными.
Традиционные подходы, используемые в математическом моделировании, такие как построение регрессионных моделей в виде системы уравнений, аддитивной или мультипликативной свертки, а также искусственные нейронные сети [1, 2, 3, 5, 7], в данном случае малопригодны из-за слишком высокой размерности математических моделей. В связи с этим в качестве инструментария для моделирования продуктивности сельскохозяйственных земель был выбран нечетко-множественный подход, программная реализация которого предусмотрена в ряде программных комплексов для компьютерного математического моделирования.
Совокупность ключевых показателей, определяющих плодородие и продуктивность сельскохозяйственных земель в острозасушливых условиях нижнего Поволжья, в частности Волгоградской области, представлена в таблице 1 [6].
Таблица 1
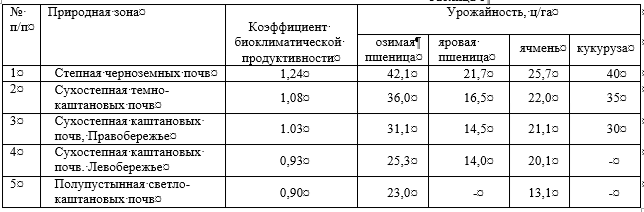
Для построения математической модели в качестве базовых моделируемых параметров были приняты коэффициент биоклиматической продуктивности и урожайность зерновых культур, которые изменялись в пределах от 0,5–1,5 и 10–45 соответственно в зависимости от природно-климатических зон.
Разработана модель для оценки продуктивности сельскохозяйственных земель, которая позволяет провести лингвистическую оценку и ранжирование рисков с учетом как качественных, так и количественных факторов. Теоретической основой модели продуктивности земель является теория нечетких множеств, предусматривающая построение функции принадлежности для моделируемых показателей, правил логического вывода с использованием значений лингвистических переменных и последующую дефаззификацию [8, 9].
Построение нечеткой модели реализовывалось в среде MATLAB с использованием модуля Fuzzy Logic Toolbox [8]. Структура разрабатываемой модели представлена на рис. 1.
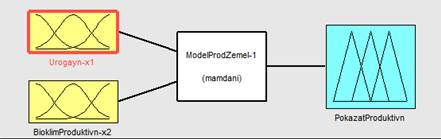
Рис. 1. Структура нечеткой модели с использованием алгоритма Мамдани
Реализация непосредственно нечеткого вывода модели осуществлялось на основе следующих стадий алгоритма Мамдани (Mamdani).
1. Фазификация — задание нечеткости с помощью функции принадлежности (ФП) для терм-множеств входных и выходных переменных на основе их лингвистических определений [3]:
x1 — лингвистическая переменная «Урожайность»;
х2 — лингвистическая переменная «Коэффициент биоклиматической продуктивности»;
y — лингвистическая переменная «Уровень продуктивности сельскохозяйственных земель».
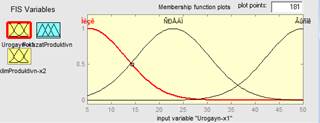
Для входной лингвистической переменной х1 и выходной у терм-множество состоит из трех термов T = {Низкий (Н), Средний (С), Высокий (В)}, которые характеризуют соответственно низкий, средний и высокий уровень этих переменных. Для входной лингвистической переменной х2 терм-множество включает два терма T = {Низкий (Н), Высокий (В)}, которые характеризуют низкий и высокий уровень этих переменных [9]. На рисунке 2 приведены графики функций принадлежности терм-множеств входных лингвистических переменных.
 а)
а) 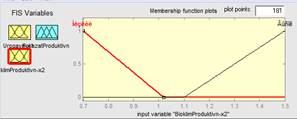 б)
б)
Рис. 2. Функции принадлежности: а) для входной переменной х1; б) для входной переменной х2
Для выходной переменной у (лингвистическая переменная «Уровень продуктивности сельскохозяйственных земель») терм-множество состоит из трех термов: Низкая продуктивность земель (LOW); Средняя продуктивность земель (MIDDLE); Высокая продуктивность (HI), представленных на рисунке 3.
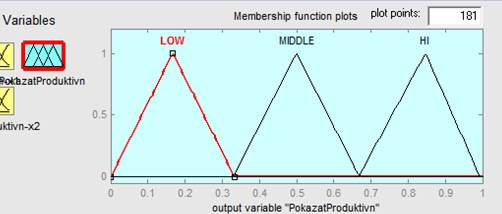
Рис. 3. Функции принадлежности для выходной переменной У
2. 3адание правил разрабатываемой модели нечетко-логического вывода. В алгоритме Мамдани база правил задана в виде структуры с двумя входами и одним выходом (рис. 1).
Правила нечетко-логического вывода, реализуемые моделью, записываются в виде «ЕСЛИ Х = а, ТО У = в» и отражают логические взаимосвязи входных лингвистических переменных хi и выходной у, где i=1,2. Эти правила формируются на основе общих теоретических представлений продуктивности сельскохозяйственных земель и позволяют смоделировать механизм логического вывода. Сформулированные правила нечетко-логического вывода представлены в таблице 1 (фрагмент).
Таблица 1
Фрагмент базы нечетких продукционных правил
|
Номер правила |
Антецедент |
Консеквент |
|
1 |
х1=Низк ˅ х2=Низк |
y= LOW |
|
2 |
х1=Средн |
y= MIDDLE |
|
3 |
х1=Высок ˅ х2=Высок |
y= HI |
Базы правил из таблицы 1 вводится в систему нечеткого вывода в окне «Rule Editor».
3. Дефазификация представляет собой процесс определения числовых значений выходной переменной.
Разработанная в среде Fuzzy Logic Toolbox система нечеткого вывода позволяет получить оценку моделируемой продуктивности сельскохозяйственных земель на этапе дефазификации.
Исходные значения входных параметров следует вводить в интерфейсе Rule Viewer окна графического вывода (рис. 4).
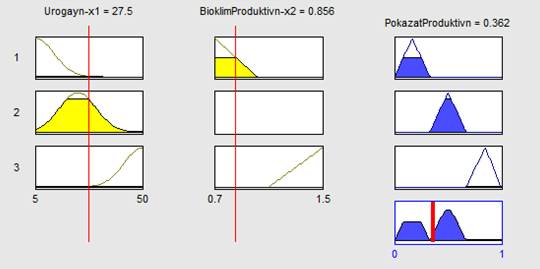
Рис. 4. Окно нечеткого вывода моделируемых показателей
При величине урожайности 27,5 ц/га значение лингвистической переменой х1 соответствует терму Средний (С). При величине х2 = 0,856 значение лингвистической переменой x2 соответствует терму Низкий (Н).
По заданным значениям х1 и x2 активизируются правила 1 и 2. Результирующее значение выходной переменной У соответствует значению 0,386.
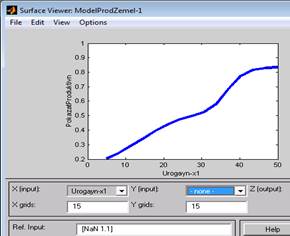 а)
а) 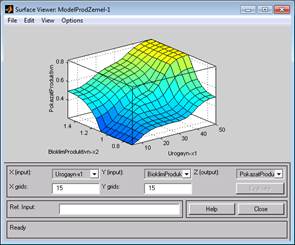 б)
б)
Рис. 5. а) График функции зависимости обобщенного показателя продуктивности земель от величины урожайности зерновых культур; б) поверхность отклика разработанной системы нечеткого вывода
На рисунке 5 представлена численная зависимость обобщенного показателя продуктивности сельскохозяйственных земель от величины урожайности зерновых культур, построенная при величине коэффициента биоклиматической продуктивности, равном 1,1, нелинейность которой определяется продукционными правилами системы нечеткого вывода.
Разработанная методом нечеткого вывода и реализованная в среде Fuzzy Logic Toolbox программного комплекса MATLAB основа нечеткого вывода обобщенных оценок продуктивности сельскохозяйственных земель обладает широкими возможностями адаптации к диапазонам возможного изменения и модельным значениям входных показателей, а также их функций принадлежности, задаваемых экспертами.
Рецензенты:
Рогачев А.Ф. д.т.н., профессор, зав. кафедрой «Математическое моделирование и информатика» ФГБОУ ВПО «Волгоградский ГАУ», г.Волгоград;
Бородычев В.В. д.с.-х.н., профессор, директор Волгоградского филиала ГНУ ВНИГиМ, г. Волгоград.
Библиографическая ссылка
Мелихова Е.В. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И ПРОГРАММНАЯ РЕАЛИЗАЦИЯ УРОВНЯ ПРОДУКТИВНОСТИ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ЗЕМЕЛЬ МЕТОДОМ НЕЧЕТКОГО ВЫВОДА // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=21438 (дата обращения: 11.02.2026).



