Постановка задачи динамической управляемости исследуемого типа манипуляторов
Динамические ограничения структуры с гибкими связями рассмотрены на основе тросового манипулятора с гибким подвесом объекта перемещения [2,3]. В каждый момент времени на любой из тросов системы действуют три силы – сила тяжести, обусловленная массой троса, сила, приложенная к тросу, наматываемому на барабан и сила, приложенная к грузу, состоящая из веса груза и сил двух тросов, участвующих в перемещении груза.
Эскиз кинематической схемы манипулятора с подвесом схвата на гибких звеньях представлен на рис. 1.
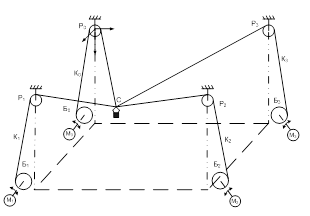
Рис. 1. Кинематическая схема манипулятора
Конструктивно манипулятор состоит из канатов К0 ÷ К3 (в дальнейшем звеньев), одни концы которых соединены в точке крепления схвата. Вторые концы звеньев пропущены через шкивы P0 ÷ P3 и закреплены на барабанах Б0 ÷ Б3 соответственно. Изменение положения схвата в пространстве достигается за счет изменения длин звеньев при вращении барабанов с помощью моторредукторов М0 ÷ М3.
В динамике данный механизм представляет собой сложную маятниковую систему [1, 4, 5]. Рассмотренные в работах [1,2] соотношения справедливы только тогда, когда все три троса находятся в напряженном состоянии. Однако в системе применяются только гибкие связи, ограничивающие возможные перемещения груза только в одном направлении. Рассмотрим плоскую систему, конструктивно схожую с исследуемой (рисунок 2). При условии ![]() и
и ![]() колебания груза соответствуют колебаниям физического маятника. В случае, когда
колебания груза соответствуют колебаниям физического маятника. В случае, когда ![]() или
или ![]() , одна из связей деформируется и начинается неуправляемое колебание не только груза, но и другой, недеформированной, связи.
, одна из связей деформируется и начинается неуправляемое колебание не только груза, но и другой, недеформированной, связи.
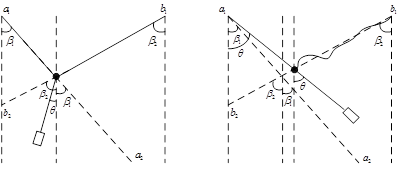
Рис. 2. Неуправляемые колебания плоской системы с гибкими связями
В исследуемом типе механизмов будут происходить аналогичные процессы. Для пространственного случая при использовании 3 тросов для манипулирования объектом зона управляемости будет ограничена четырьмя плоскостями: тремя плоскостями, образованными прямыми, которые содержат гибкие связи и плоскостью основания зоны обслуживания. Если центр масс груза при колебательных движениях вышел за границы этой зоны, то система становится неуправляемой.
Получение аналитических выражений, описывающих зону управляемости.
Рассмотрим геометрические соотношения, позволяющие оценить параметры, влияющие на управляемость системы (рис. 3).
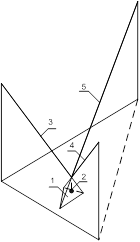
Рис. 3. Геометрическое представление зоны регулирования
1-зона управляемости, 2 – центр масс груза, 3,4,5 – гибкие связи
Составим уравнения плоскостей, образованных парами связей. Обозначим X и Y – геометрические размеры зоны обслуживания; xкр, yкр, zкр – координаты точки крепления груза; xгр, yгр, zгр – координаты центра масс груза; ψx, ψy, ψz – углы между вектором скорости и соответствующими ортами системы координат; l – расстояние между точкой крепления и центром масс груза. Для тросов 0 и 1:
![]()
Для тросов 1 и 2:
![]()
Для тросов 2 и 3:
![]()
Для тросов 0 и 3:
![]()
Для тросов 0 и 2:
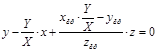
Для тросов 1 и 3:
![]()
Определим зависимость координат центра масс груза от скорости и направления движения, для этого воспользуемся соотношением.
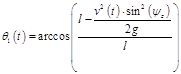 (1)
(1)
Тогда:
![]() (2)
(2)
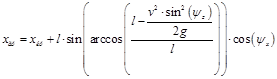 (3)
(3)
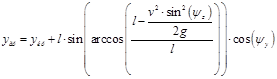 (4)
(4)
Поскольку центр масс груза не должен пересекать плоскости, образованные соответствующими прямыми, а, следовательно, координата по оси z груза должна быть больше, чем соответствующая ее координата z плоскости с координатами x и y, равными координатам груза соответственно, то систему неравенств удобней составлять относительно координаты z. Преобразуем соответствующие уравнения плоскостей.
Для тросов 0 и 1:
![]() (5)
(5)
Для тросов 1 и 2:
![]() (6)
(6)
Для тросов 2 и 3:
![]() (7)
(7)
Для тросов 0 и 3:
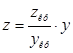 (8)
(8)
Для тросов 0 и 2:
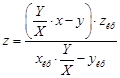 (9)
(9)
Для тросов 1 и 3:
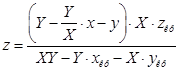 (10)
(10)
Составим для примера систему неравенств для 0,1 и 2 тросов (11). Система неравенств, связывающая скорость, направление движения и текущие координаты точки подвеса груза с возможностью управления системой:
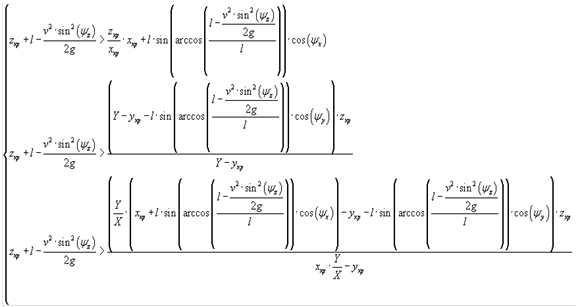 (11)
(11)
Построим компьютерную модель, позволяющую оценить распределение зоны управляемости. Анализ результатов моделирования показал, что максимальное отклонение груза будет в случае, когда вектор ![]() лежит в плоскости, параллельной плоскости XY. Кроме того, вектор должен лежать в вертикальной плоскости, перпендикулярной плоскости пересечения и расстояние от него до плоскости должно быть минимальным. Рассмотрим полуплоскости с рабочими тросами 012 и 023 при z = 1.25 м. Размеры зоны обслуживания X и Y возьмем в соответствии с размерами созданного для исследований натурного макета (X = 2.5 м, Y = 1.3 м).
лежит в плоскости, параллельной плоскости XY. Кроме того, вектор должен лежать в вертикальной плоскости, перпендикулярной плоскости пересечения и расстояние от него до плоскости должно быть минимальным. Рассмотрим полуплоскости с рабочими тросами 012 и 023 при z = 1.25 м. Размеры зоны обслуживания X и Y возьмем в соответствии с размерами созданного для исследований натурного макета (X = 2.5 м, Y = 1.3 м).
Результаты моделирования и заключение
Определим для данной плоскости граничные значения скорости (рис. 4):
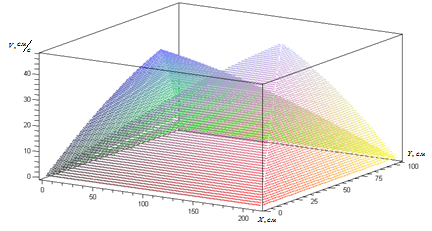
Рис. 4. Зависимость максимальной скорости регулирования от положения точки подвеса в плоскости зоны обслуживания
Анализ полученного распределения показывает, что значение максимальной рекомендуемой скорости варьируется в значительных пределах в зависимости от положения точки крепления в горизонтальной плоскости X0Y. Вид зависимости, исходя из неравенств на рис. 3, математически не зависит от массы груза и приложенных к тросам сил (считаем, что предельную скорость манипулятор может обеспечить), и характер распределения максимальной рекомендуемой скорости при изменении данных параметров будет таким же.
На рис. 5 представлена зависимость рекомендуемой максимальной скорости от положения точки крепления груза по вертикали при x = 50 см, y = 50 см. Диапазон изменения координаты z был выбран исходя из конструкции макета для проведения натурных испытаний.
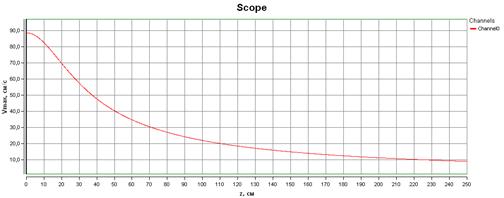
Рис. 5. Зависимость максимальной скорости регулирования от положения точки подвеса груза по вертикали
Вид зависимости максимальной скорости регулирования от положения точки крепления по вертикали имеет экспоненциальный характер. При этом представленные в данной статье математические соотношения показывают, что относительно вертикальной оси максимальная возможная скорость будет меняться пропорционально изменению площади зоны обслуживания и общий вид зависимости при проектировании реальных манипуляторов со значительной площадью обслуживания будет сохраняться. При увеличении высоты зоны обслуживания манипулятора зона управляемости уменьшается. При соблюдении ограничений по скорости регулирования положение точки крепления груза будет стабильным и колебательные процессы не будут распространяться на гибкие звенья механизма.
Работа выполнена в рамках гранта (проекта) РФФИ № 14-084-3148.
Рецензенты:
Прокопенко Н.Н., д.т.н., профессор, зав. кафедрой «ИСиРТ», зам. директора по НИР, ФГБОУ ВПО «ИСОиП (филиал) ДГТУ», г. Шахты;
Сапронов А.А., д.т.н., профессор, генеральный директор ООО Научного предприятия «Электронные информационные системы», р.п. Каменоломни.
Библиографическая ссылка
Валюкевич Ю.А., Алепко А.В., Дубовсков В.В., Яковенко Д.М. ОПРЕДЕЛЕНИЕ ДИАПАЗОНА ДИНАМИЧЕСКОЙ УПРАВЛЯЕМОСТИ МАНИПУЛЯТОРА С ГИБКИМИ СВЯЗЯМИ // Современные проблемы науки и образования. 2015. № 2-2. ;URL: https://science-education.ru/ru/article/view?id=21431 (дата обращения: 28.02.2026).



