Математические модели, возникающие при изучении ряда прикладных задач, приводят к необходимости решения краевых задач для нагруженного дифференциального уравнения третьего рода. Такие примеры можно найти в математической физике, математической биологии и других областях.
В работе изучен численный метод решения краевой задачи третьего рода для нагруженного оператора Штурма-Лиувилля. Для этой задачи установлены условия однозначной разрешимости.
В настоящей работе будем изучать численный метод решения задачи
(1)
(2)
(3)
где 
– оператор Штурма-Лиувилля, 
– фиксированная точка интервала 
, 
и 
– положительные числа. Коэффициент 
в уравнении (1) предполагается отличной от нуля хотя бы в одной точке 
.
Определим условия однозначной разрешимости задачи (1)-(3).
Теорема 1. Пусть 
и для всех 
выполнено условие
. (4)
Тогда решение задачи (1)-(3) существует, единственно и принадлежит классу 
.
Пусть 
и 
– решения задач:
, (5)
. (6)
Отметим, что задачи (5), (6) при выполнении условий теоремы 1 однозначно разрешимы и их решения принадлежат классу . Как установлено в работе [1], необходимым и достаточным условием однозначной разрешимости задачи (1)-(3) является условие
(7)
при этом её решение 
представляется через решения задач (5) и (6) в виде:
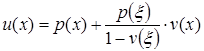. (8)
Покажем, что выполнение условия (4) гарантирует (7), что достаточно для однозначной разрешимости задачи (1)-(3). Введем обозначение
(9)
и оценим снизу выражение 
. С этой целью получим верхнюю оценку наибольшего значения 
решения задачи (6) на 
. Из принципа максимума [2], [6] для задачи (6) и условий на 
следует, что 
для всех . Наибольшее значение функции не достигается в точках 
и 
в силу краевых условий.
Пусть 
– точка максимума . Из равенства
(10)
в силу 
следует [3]:
.
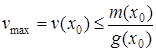Тогда
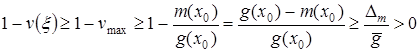. (11)
Теорема доказана.
Далее будем считать, что выполнены условия B: 
Имеет место
Теорема 2. Если выполнены условия В и (4), то решение задачи (1)-(3) принадлежит классу 
.
Перейдем к численному решению задачи (1)-(3). На отрезке [0,1] введем равномерную сетку 
Шаг 
сетки выберем меньше половины меньшего из отрезков 
Номер 
выберем из условия 
Пусть сеточная функция 
– решение конечно-разностной задачи
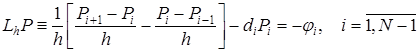, (12)
а сеточная функция 
– решение конечно-разностной задачи
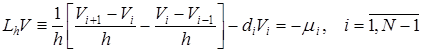, (13)
где
(14)
Введем обозначения:
(15)
, (16)
и в качестве приближенного решения задачи (1)-(3) на сетке 
выберем функцию 
, которая выражается через решения задач (13) и (14) по формуле
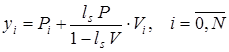. (17)
Имеет место
Теорема 3. Пусть выполнены условия B и (4). Тогда сеточная функция , определенная по формуле (17), сходится при 
к решению задачи (1)-(3) со вторым порядком точности по шагу 
в равномерной метрике.
Получим априорную оценку погрешности 
в равномерной метрике на сетке . Пользуясь представлением (8) решения задачи (1)-(3), получаем:
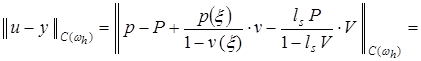
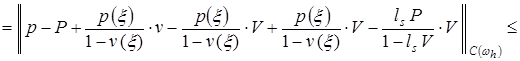
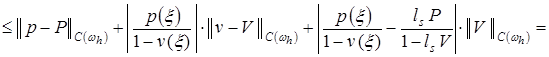
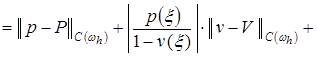
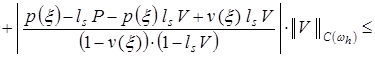
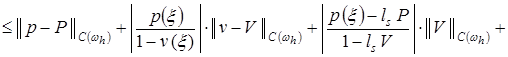
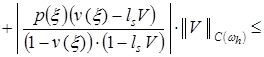
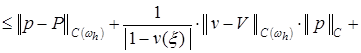
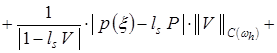
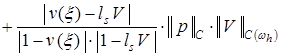. (18)
Оценим слагаемые в правой части (18). Как известно [4], конечно-разностные схемы (12) и (13) сходятся соответственно к решениям дифференциальных задач (5) и (6) с порядком 
, и, следовательно, существуют положительные постоянные 
и 
, не зависящие от , что
. (19)
Значения 
и 
аппроксимируются 
и 
соответственно с точностью [5], то есть существуют 
и 
, не зависящие от , что
. (20)
Для решения задачи (5) известна априорная оценка:
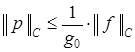. (21)
Учитывая (10), из априорной оценки
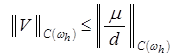
получаем:
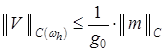. (22)
Получим нижнюю оценку выражения 
. Заметим, что в силу (14), 
. Оценим сверху максимальное значение 
сеточной функции 
. В силу условий на коэффициенты и правую часть задачи (13), для неё имеет место принцип максимума третьей разностной краевой задачи [4], из которой следует, что 
. Если 
, где 
, то в силу 
, из уравнения (13) получаем оценку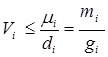 
. Если 
, то из левого краевого условия (13) следует, что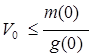 
. Если 
, то из краевого условия (13) следует, что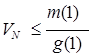 
. Таким образом, если 
, то
.
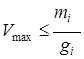Тогда
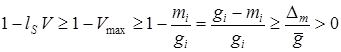. (23)
Применяя оценки (19)-(23), из (18) получаем:
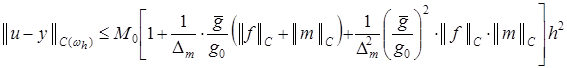, (24)
где 
.
Из априорной оценки (24) следует доказательство теоремы 3.
При 
, в силу принципа максимума для задачи (6), 
, и в силу принципа максимума для задачи (13), 
. В этом случае 
, и, как следует из (24), 
. Аналогичный результат получен в работе [2].
При 
может наблюдаться неустойчивость решения задачи (1)-(3), а предположенный численный метод может быть непригодным для ее решения с требуемой точностью. Например, если 
для всех 
, то, как следует из оценки (24), 
. В этом случае выход состоит в решении задач (5) и (6) с более высоким порядком точности, чем 
, а также в аппроксимации значений 
и 
соответствующего порядка.
Рецензенты:
Шхануков-Лафишев М.Х., д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления Кабардино-Балкарского, г. Нальчик;
Ашабоков Б.А., д.ф.-м.н., профессор Высокогорного Геофизического Института, г. Нальчик.
Библиографическая ссылка
Абрегов М.Х., Нахушева Ф.М., Бечелова А.Р. ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ТРЕТЬЕГО РОДА ДЛЯ НАГРУЖЕННОГО ОПЕРАТОРА ШТУРМА-ЛИУВИЛЛЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18715 (дата обращения: 04.11.2025).