Совершенствование бинарных парогазовых установок (ПГУ) связано с повышением температуры газа перед газовой турбиной, начальных параметров пара, усложнением тепловых схем установок, комбинированной выработкой электрической и тепловой энергии, реализацией их конкурентных преимуществ (в частности, термодинамической эффективности и маневренных характеристик) в системах теплоэнергоснабжения. Большой комплекс научных исследований в обоснование создания ПГУ высокой энергетической эффективности проведен научными школами ОАО ВТИ, НИУ «МЭИ», Саратовского ГТУ имени Гагарина Ю.А., Ивановского и Новосибирского ГТУ и другими организациями. Указанными исследованиями установлено, что повышение термодинамической эффективности ПГУ связано с усложнением их схем и приводит к снижению надежности работы ПГУ в системах теплоэнергоснабжения [1-4].
Управление надежностью при создании энергетического оборудования, установок в целом и систем энергообеспечения на их основе с целью оптимизации конструктивных, технологических, схемных и эксплуатационных решений требует разработки методов и методик расчета единичных показателей надежности (ПН) элементов энергооборудования, главным образом безотказности. Поэтому расчет ПН элементов энергооборудования ПГУ должен базироваться на основе вероятностных методов, позволяющих учесть статистическое рассеяние характеристик прочности и нагруженности с использованием теории случайных величин и случайных функций. Модели надежности энергооборудования и энергоустановок в целом создаются на основе анализа их функционального назначения с учетом действительных факторов и условий работы, достоверности исходной информации, требуемой точности результата оценки надежности. Поэтому методы расчета показателей надежности ПГУ и систем теплоэнергоснабжения на их основе должны базироваться на вероятностных моделях, учитывающих как схемные решения, так и требования потребителей по покрытию электрических и тепловых нагрузок. Разработанный авторами в [3,4] комплекс вероятностных методов и моделей расчета единичных, комплексных и интегральных ПН позволил выявить влияние термодинамических параметров и расходных характеристик рабочих тел, конструктивных и схемных решений на их численные значения, что позволяет учесть факторы надежности при оптимизации параметров и схемных решений ПГУ. Очевидно, что точность полученных расчетных значений ПН элементов оборудования и ПГУ в целом определяется точностью математических моделей, точностью принимаемых исходных данных и погрешностью расчетов, т.е. расчетные значения ПН являются вероятностно неопределенными. Таким способом ставится задача учета неопределенности расчетных значений ПН элементов энергооборудования, ПГУ в целом и систем теплоэнергоснабжения на выбор оптимальных параметров и устойчивость полученных оптимальных решений.
Основные методические положения
Задача оптимизации термодинамических параметров рабочих тел, конструктивных характеристик оборудования и схемных решений отопительных ПГУ в системах теплоэнергоснабжения ставится следующим образом: максимизировать (минимизировать) критерий оптимальности R [X, Y, Z] при условии, что расчетные значения принятых ПНр окажутся не ниже нормативных (оптимальных) значений ПН*, т.е.:
R [X, Y, Z] → max (min) при условии ПНр ≥ ПН*, (1)
где X, Y, Z – соответственно, комплекс оптимизируемых термодинамических параметров рабочих тел, конструктивных характеристик оборудования и схемных и компоновочных решений, заданных внешних условий функционирования ПГУ в системах теплоэнергоснабжения и исходных технико-экономических факторов.
Расчетные значения принятых ПНр определяются схемными решениями ПГУ, значениями комплексных и единичных показателей надежности элементов основного энергетического оборудования.
Решение поставленной задачи рассмотрим на примере оптимизации термодинамических параметров и схемных решений структурно сложных ПГУ с комбинированной выработкой электрической и тепловой энергии в условиях, когда расчетные значения показателей надежности отдельных элементов ПГУ являются вероятностно неопределенными. Как показано в [3], рассчитанные значения интенсивностей отказов котла-утилизатора ПГУ λ являются случайными величинами. Точность расчетов значений λ определяется точностью математической модели термонапряженного состояния трубного пучка КУ, точностью принятого метода расчета безотказности и точностью исходных данных и расчетов. Это обусловливает неопределенность полученных решений, т.е. неопределенность исходной информации о значениях безотказности трубного пучка КУ при расчете значений коэффициентов готовности КГ, блока ПГУ в целом. Все это определяет необходимость решения задачи оптимизации термодинамических параметров и технических решений в условиях неопределенности.
В основу учета неопределенности информации о рассчитанных значениях интенсивностей отказов КУ λ положено следующее. Рассчитанные значения коэффициентов готовности КГ, зависящие от интенсивности отказа трубного пучка λ, представляются случайной величиной, распределенной по нормальному закону с параметрами Мк0 и S0, дифференциальная функция которой запишется как р (к/МК0, S0). Здесь МК0 есть математическое ожидание показателя надежности ПГУ (например, значение коэффициента готовности блока КГ), а S20 - дисперсия случайной величины к. Для плотности вероятности р (к/МК0, S0) справедливы соотношения
![]() (2)
(2)
Если критерий эффективности выбора оптимальных параметров и технических решений, например чистого дисконтированного дохода (ЧДД), представить в виде R(х, к), где каждое значение к реализуется с вероятностью р (к/МК0, S0), то ожидаемое значение критерия эффективности ![]() определится как
определится как
![]() (3)
(3)
где х – оптимизируемый термодинамический параметр рабочего тела или техническое (схемное) решение.
Пусть «истинное» значение показателя надежности к1, полученное по результатам эксплуатации ПГУ, также является случайной величиной, плотность вероятности которой запишется в виде р(к/МК1, S1). При этом следует отметить, что эта функция обладает свойствами аналогичными (2). Кроме того, истинное значение величины к1 может быть как больше, так и меньше расчетного значения к0, однако априори информативность значения к1, полученного по результатам эксплуатации, существенно выше, чем для расчетного к0, т.е. S1 значительно меньше S0. Информативность значений к0 и к1 оценивается коэффициентом вариации ν, определяемого как отношение [4]
![]() . (4)
. (4)
Значения MК1 и S1 можно оценить, пользуясь плотностью вероятности получения к1 в виде р(MК1/ MК0, S0, S1). Для приведенных плотностей вероятностей справедливо равенство:
![]() (5)
(5)
Тогда по аналогии с (3) ожидаемое значение критерия эффективности R(х,к) при истинных значениях MК1 и S1 запишется в виде:
![]() (6)
(6)
Из (3) и (6) следует, что значения оптимальных параметров и технических решений, определенных по максимуму критериев ![]() и
и ![]() , различны. Кроме того, для расчетных значений к0 и истинных значений к1 величины ожидаемых значений
, различны. Кроме того, для расчетных значений к0 и истинных значений к1 величины ожидаемых значений ![]() и
и ![]() также различны.
также различны.
Для определения влияния неопределенности информации о показателях надежности КУ на изменение оптимальных параметров и технических решений разложим целевую функцию вблизи экстремума, определенного при математическом ожидании показателя надежности MК0, в ряд и ограничимся квадратными членами разложения:
![]() (7)
(7)
где ![]() и
и ![]() — первая и вторая производные критерия эффективности по к;
— первая и вторая производные критерия эффективности по к; ![]() и
и ![]() - первая и вторая производные критерия эффективности по х;
- первая и вторая производные критерия эффективности по х; ![]() - производная критерия эффективности по к и х.
- производная критерия эффективности по к и х.
Интегрируя выражение (7) с учетом плотности вероятности р (к/МК0, S0), получим:
![]() (8)
(8)
Максимум критерия эффективности R(х,к) соответствует х = х![]() , тогда:
, тогда:
![]() . (9)
. (9)
Интегрируя выражение (7) с учетом плотности вероятности р(к/МК1, S1) и принимая во внимание соотношение (3) и (6), получим:
![]() (10)
(10)
Оптимальное значение х при истинных значениях показателя надежности к с учетом (6) и (10) определится как:
![]() (11)
(11)
Максимум критерия эффективности при истинных значениях показателя надежности к определится как:
![]() (12)
(12)
где ![]() — разность дисперсий случайных величин значений расчетных и «истинных» показателей надежности к, и
— разность дисперсий случайных величин значений расчетных и «истинных» показателей надежности к, и ![]() является мерой повышения информативности о неопределенности информации о показателях надежности.
является мерой повышения информативности о неопределенности информации о показателях надежности.
Из (9), (11) и (12) следует, что степень изменения оптимизируемого параметра х в зависимости от изменения показателя надежности определится как:
![]() (13)
(13)
а разность максимальных значений критериев эффективности составит:
![]() (14)
(14)
Анализ (14) показывает, что если решается задача только учета неопределенности информации о значениях показателей надежности при оптимальных параметрах или технических решениях, то величина ![]() зависит от величины и знака
зависит от величины и знака ![]() и значения
и значения ![]() . Принимая во внимание то обстоятельство, что истинное значение к1 более информативно, чем к0, т.е.
. Принимая во внимание то обстоятельство, что истинное значение к1 более информативно, чем к0, т.е. ![]() больше нуля, то знак величины
больше нуля, то знак величины ![]() определяется знаком
определяется знаком ![]() .
.
Таким образом, величина ![]() зависит как от значений
зависит как от значений ![]() , так и от изменения информативности «истинных» и расчетных значений показателей надежности, которая определяется значениями коэффициентов вариации.
, так и от изменения информативности «истинных» и расчетных значений показателей надежности, которая определяется значениями коэффициентов вариации.
Расчетно-теоретические исследования
Разработанные методические положения учета неопределенности информации о показателях надежности КУ ПГУ использованы для оценки устойчивости оптимальных решений при определении сравнительной эффективности отопительных ПГУ, выполненных по схемам с одноконтурным, двухконтурным и трехконтурным котлами-утилизаторами электрической мощностью 110 МВт. Сравнительный анализ эффективности проведен для схем бинарных ПГУ, отличающихся числом уровней давлений генерируемого в КУ пара и выполненных на базе ГТУ типа PG6111FA фирмы General Electric мощностью 77 МВт со следующими характеристиками: степень повышения давления в компрессоре 15,8, расход воздуха через компрессор 203,3 кг/с, температура продуктов сгорания после турбины 600оС. В качестве паровой принята турбина типа Т- 25/33-7,6/0,12 ОАО «Калужский турбинный завод» с параметрами свежего пара высокого давления 8,6 МПа и 535 ОС. В основу расчета конструктивных характеристик КУ положен разработанный и зарегистрированный программный комплекс [5]. В таблице 1 представлены результаты расчетов энергетических характеристик отопительной ПГУ при различных температурах наружного воздуха. При этом тепловая мощность ПГУ при расчетной температуре наружного воздуха составляет 89,5 МВт.
Таблица 1
Энергетические характеристики отопительной ПГУ, выполненной по различным схемам
|
Наим. |
Температура наружного воздуха |
Мощность ГТУ |
Мощность ПТУ |
Тепловая мощность газоводяного подогревателя |
Тепловая мощность отборов пара |
|
|
(°С) |
(МВт) |
(МВт) |
(МВт) |
(Гкал/ч) |
|
Одноконтурный КУ |
+30 |
66,70 |
27,08 |
5,97 |
21,58 |
|
+15 |
77,42 |
25,59 |
6,45 |
21,59 |
|
|
-1,8 |
85,97 |
22,03 |
6,88 |
70,50 |
|
|
-26 |
89,18 |
19,33 |
7,83 |
70,80 |
|
|
Двухконтурный КУ |
+30 |
66,70 |
31,24 |
5,97 |
21,58 |
|
+15 |
77,42 |
31,42 |
6,45 |
21,59 |
|
|
-1,8 |
85,97 |
22,90 |
6,88 |
70,50 |
|
|
-26 |
89,18 |
19,79 |
7,83 |
70,80 |
|
|
Трехконтурный КУ |
+30 |
66,70 |
31,29 |
5,97 |
21,58 |
|
+15 |
77,42 |
33,55 |
6,45 |
21,59 |
|
|
-1,8 |
85,97 |
25,28 |
6,88 |
70,50 |
|
|
-26 |
89,18 |
22,11 |
7,83 |
70,80 |
Полученные показатели энергетической эффективности использованы для расчета величины ЧДД сравниваемых вариантов отопительной ПГУ, которые приведены в таблице 2. Из таблицы следует, что наиболее эффективной является схема ПГУ с трехконтурным КУ.
Таблица 2
Показатели эффективности ПГУ, выполненных по различным схемам
|
Наименование |
Обознач. |
Ед.изм. |
I давление |
II давления |
III давления |
|
Мощность ПГУ |
NПГУ |
МВт |
103,02 |
108,84 |
110,6 |
|
Электрический КПД ПГУ |
ηПГУ |
- |
0,4711 |
0,4977 |
0,5074 |
|
Коэффициент готовности ПГУ |
КГ |
- |
0,9758 |
0,9629 |
0,9493 |
|
Чистый дисконтированный доход |
ЧДД |
млн руб. |
1956,2 |
2156,7 |
2849,4 |
|
Изменение ЧДД |
ΔЧДД |
млн руб. |
273,10 |
193,40 |
0,0000 |
С использованием разработанной методики с учетом (14) проведено исследование влияния неопределенности и информативности исходной информации о значениях коэффициента интенсивности отказа КУ на сравнительную эффективность различных схем ПГУ. Результаты расчетов представлены на рисунке 1.
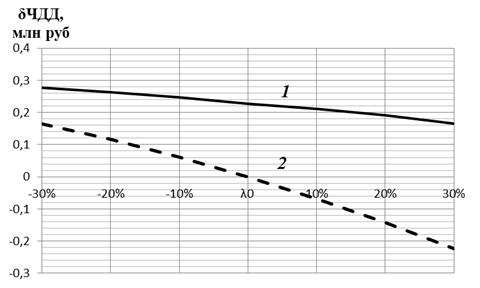
Рис. 1. Влияние неопределенности и информативности показателя безотказности
КУ ПГУ на изменение величины ЧДД: 1- величина информативности «истинного» значения коэффициента безотказности![]() = 0,5
= 0,5 ![]() ; 2 -величина информативности «истинного» значения коэффициента безотказности
; 2 -величина информативности «истинного» значения коэффициента безотказности ![]() =
= ![]() .
.
Из рисунка 1 следует, что повышение информативности «истинного» значения коэффициента интенсивности отказа КУ приводит к повышению ожидаемого значения величины ЧДД. Кроме того, отклонение «истинного» значения интенсивности отказа на 20% приводит к изменению ЧДД на 0,1-0,5 млн руб. Приведенные значения влияния неопределенности информации о расчетных значениях интенсивности отказа КУ существенно ниже значений изменения величины ЧДД при переходе от схемы с трехконтурным КУ к схеме с двухконтурным КУ. Это свидетельствует об устойчивости вывода об экономической эффективности схемы ПГУ с трехконтурным КУ.
Заключение
1. Разработана вероятностная методика учета неопределенности информации о единичных и комплексных показателях надежности энергетического оборудования парогазовых установок на выбор рациональных схемно-параметрических решений.
2. Установлено, что повышение информативности «истинных» показателей надежности приводит к повышению эффективности принятых оптимальных технических решений. Отклонение «истинных» значений показателей надежности ПГУ в сторону отрицательных значений приводит к снижению численных значений критерия эффективности.
3. Неопределенность и информативность расчетных значений интенсивности отказов не оказывают влияния на вывод об экономической эффективности ПГУ с трехконтурным котлом-утилизатором.
Работа выполнена при финансовой поддержке Минобрнауки РФ по НИР № 1579 в рамках государственного задания
Рецензенты:
Хрусталев В.А., д.т.н., профессор кафедры «Тепловые и атомные электрические станции» ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.», г. Саратов;
Семенов Б.А., д.т.н., профессор, заведующий кафедрой «Промышленная теплотехника» ФГБОУ ВПО «Саратовский государственный технический университет имени Гагарина Ю.А.», г. Саратов.
Библиографическая ссылка
Анкудинова М.С., Ларин Е.А., Обозов К.Э. МЕТОД УЧЕТА НЕОПРЕДЕЛЕННОСТИ ИНФОРМАЦИИ О НАДЕЖНОСТИ ПРИ ОПТИМИЗАЦИИ СХЕМ И ПАРАМЕТРОВ ПГУ В СИСТЕМАХ ТЕПЛОЭНЕРГО-СНАБЖЕНИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18271 (дата обращения: 12.03.2026).



