В работах [2, 3] и [1, 4] рассмотрены две различные математические модели для описания свободной конвекции в воздушном зазоре навесных вентилируемых фасадов (НВФ). Хотя они обе основаны на приближении Буссинеска, варианты которого подробно изложены в [5], тем не менее в основе их лежат разные дифференциальные уравнения. Кроме того, они основаны на различных дополнительных допущениях.
В обеих моделях рассматривается плоский, вертикальный слой воздуха заданной ширины и высоты, соответствующим ширине воздушного зазора и высоте здания. Ось z – направлена вверх, а ось х – горизонтально поперек зазора (рис.1).
Плотности тепловых потоков через стенки зазора q1 и q2 (рис.1), а отношение их проекций на ось х: 
.
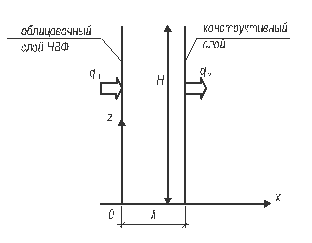
Рис. 1. К постановке задачи для плоского слоя.
В обеих моделях предполагается, что скорость имеет только вертикальную составляющую и зависит только от координаты х.
Избыточная температура Т, по сравнению с температурой внизу зазора, в первой модели [2, 3] зависит только от х, а во второй модели [1, 4] от х и z.
Избыточное давление р, по сравнению с барометрическим атмосферным, в обеих моделях зависит только от z.
При обезразмеривании основных величин так, как принято в работе [3], распределение скорости по первой модели имеет вид [1, 2]:
, (1)
а распределение температуры:
. (2)
Распределение скорости по второй модели [1, 4] имеет следующий вид [4]:
, (3)
где коэффициенты С1 и С2 определяются по формулам 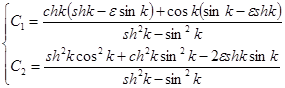[4]:
, (4)
Трансцендентное уравнение для определения k, входящего в формулы (3) – (4), имеет вид [4]:
, (5)
где R – число Релея. Распределение температуры для второй модели имеет вид [4]:
, (6)
Сравнивая формулу (1) с формулой (3) и формулу (2) с (6) трудно предположить, что в некотором предельном случае они совпадут.
Отметим также разницу в дополнительных допущениях обеих моделей. В первой модели предполагается, что расход поперек воздушного зазора равен нулю [3]:
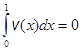, (7)
Условие (7) представляется естественным для свободной конвекции в зазоре с горизонтальными рассечками.
Во второй модели требования (7) – нет. Дополнительными допущениями этой модели является отсутствие прогрева слоя воздуха в самом низу зазора [1, 4]:
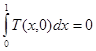, (8)
Основанием для гипотезы об эквивалентности этих двух моделей при ε→1 могут являться графики скорости и температуры, приведенные в работе [4] для ε = 0,8. Они довольно близки к графикам функций (1) и (2) – соответственно. Для того чтобы найти выражения для скорости и температуры при ε = 1, сначала необходимо найти k, соответствующее значению ε = 1.
Для данного значения ε = 1 формулы для коэффициентов С1 и С2 (4), после преобразований примут вид:
(9)
Тогда уравнение для определения k (5), после преобразований, можно записать в виде:
. (10)
Единственным решением этого уравнения в области действительных чисел является k = 0. Это же подтверждается графиком левой части уравнения (10), приведенным на рис. 2. Таким образом, при ε = 1 
k = 0 для любых чисел Релея R.
При k = 0 невозможно непосредственно получить значения С1 и С2, а также вид функций скорости и температуры, т. к. выражения (9), (3), (6) приводят к неопределенности типа 
. Тем не менее имеется возможность рассчитать скорость при малых k по формуле (3), где координаты С1 и С2 находятся по формулам (9).
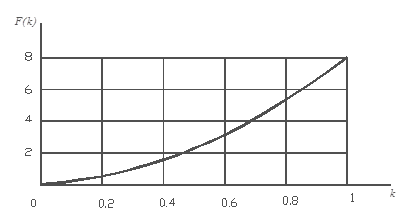
Рис. 2. График левой части уравнения (10)
На рис. 3 приведены графики распределения скорости. Из этого рисунка видно, что при k = 0,01 графики скорости, построенные по зависимостям (1) и (3), совпадают с точностью до графического разрешения. Это еще раз подчёркивает правомерность выдвинутой гипотезы о
совпадении математической модели [1, 4] с моделью [2, 3] при ε→1.
После преобразований формулы (3) при ε = 1 получим следующие выражение для скорости:
, (11)
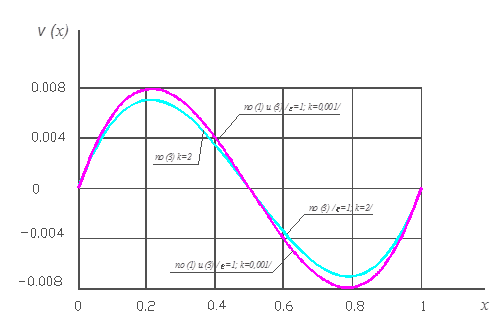
Рис. 3. Распределение скорости поперек воздушного зазора, рассчитанные по формулам (1) и (3) при ε = 1 и различных k.
Входящие в формулу (11) выражения необходимо разложить в ряд Тейлора для малых k, а
значит и kх, т. к. 0 ≤ х ≤ 1. Разложение тригонометрических и гиперболических функций по малому параметру k дает:
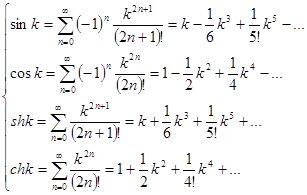, (12)
Получим разложение в ряд Тейлора для комбинаций этих функций, которые входят в выражение для v(х) (11) и войдут для Т(х) (6).
, (13)
где
,
Если в (13) обозначить n = 2l; l = 0, 1, 2, 3…; то формула (13) примет вид:
, (14)
Аналогично, получим следующие выражения:
, (15)
, (16)
Для произведений гиперболических и тригонометрических функций, с учетом (12), получим следующие выражения:
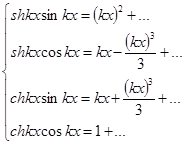, (17)
Используя формулы (12), (16), (17), выражение для скорости (11) примет вид:
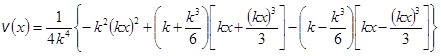, (18)
Окончательно, из (18) получаем:
, (19)
Выражение (19) полностью совпадает с выражением (1).
Далее рассмотрим выражение для температуры (6), которое при ε = 1 примет вид:
, (20)
С учетом разложений гиперболических и тригонометрических функций в ряд Тейлора (12) – (17), можно записать
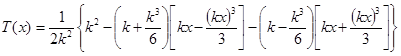, (21)
Или окончательно, при k→0:
, (22)
Видно, что формула (22) полностью совпадает с формулой (2).
Таким образом, распределение скорости и температуры (3) и (6) переходят в распределение (1) и (2) при ε = 1. Отметим, что ε = 1 соответствует случаю, когда тепловой поток через облицовочный слой НВФ равен по величине и направлению тепловому потоку через конструктивный слой. В этом случае, в частности, получаем линейное распределение температуры поперек воздушного зазора, а распределение скорости соответствует нулевому расходу, т.е. в зазоре должны быть как восходящие, так и нисходящие потоки воздуха.
В заключение заметим, что плотность теплового потока q1 определяется температурами атмосферы и внутри зазора, термическим сопротивлением облицовки и радиационным тепловым потоком. Плотность теплового потока q2 определяется температурами внутри зазора и здания, а также термическим сопротивлением конструктивного слоя.
Математическая модель, принятая в работах [1, 4], является более общей. В частном случае (q1 = q2), она переходит в математическую модель работ [2, 3].
Рецензенты:
Зуев В.А., д.т.н., профессор, заведующий кафедрой «Кораблестроение и авиационная техника» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород;
Грамузов Е.М., д.т.н., профессор, заведующий кафедрой «Аэро-гидродинамика, прочность машин и сопротивление материалов» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Библиографическая ссылка
Косолапов Е.А., Федотов А.Б., Машенков А.Н. АСИМПТОТИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ ДВУХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СВОБОДНОЙ КОНВЕКЦИИ В ВОЗДУШНОМ ЗАЗОРЕ НАВЕСНЫХ ФАСАДОВ ЗДАНИЙ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18064 (дата обращения: 19.04.2024).