Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Борзых В.Э. 1 Шалкина Т.Н. 2 Николаева Д.Р. 1

---

1 ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет»

2 ФГБОУ ВПО «Тюменский государственный нефтегазовый университет»

В статье рассмотрен подход к разработке математической модели оценивания профессиональных компетенций студентов ВУЗа в процессе профессиональной подготовки. Обосновывается актуальность и значимость оценки сформированности профессиональной компетентности выпускников ВУЗа. Определены покомпонентные критерии, уровни их сформированности и представлена к рассмотрению модель оценки профессиональной компетентности выпускников ВУЗа. На основе описанной модели разработана система измерения профессиональной компетентности обучаемого. Выделены этапы моделирования процесса построения математической модели измерения, а также приведены основные алгоритмы оценки профессиональной компетентности. В статье предложен новый оригинальный подход в области построения модели оценивания профессиональных компетенций, основанный на теории. Представлены результаты экспериментального исследования по определению наиболее статистически значимой модели оценивания профессиональных компетенций с применением множественного корреляционно-регрессионного анализа.

Статья в формате PDF

172 KB

анализ размерностей

теория подобия

система оценивания

профессиональная компетенция

математическая модель

1. Алабужев П.М. Теория подобия и размерностей. Моделирование : учебное пособие для вузов / П.М. Алабужев, В.Б. Геронимус, Л.М. Минкевич. – М.: Высшая школа, 1968. – 208 с.

2. Аскеров Э.М. Автоматизация многокритериального оценивания профессиональных компетенций будущих специалистов / Э.М. Аскеров, И.Д. Рудинский // Информатизация образования и науки. – 2008. – № 3 (7). – С. 82-89.

3. Заварихин А.Е. Разработка моделей и инструментальных средств управления образовательной деятельностью (на примере дистанционной технологии обучения для экономических специальностей): дис. ... канд. экон. наук: 08.00.13 / А.Е. Заварихин. – Оренбург, 2004. – 184 с.

4. Махныткина О.В. Моделирование и оптимизация индивидуальной траектории обучения студента : автореф. дис... канд. тех. наук: 05.13.10 / О.В. Махныткина. – Новосибирск, 2013. – 23 с.

5. Попов Г.В. Оценка профессиональных компетенций / Г.В. Попов, Т.В. Забегалина, Л.И. Назина // Методы менеджмента и качества. – 2007. – № 6. – С. 40-43.

6. Сибикина И.В. Модели и алгоритмы формирования и оценки компетенций выпускника вуза : автореф. дис... канд. тех. наук: 05.13.10 / И.В. Сибикина. – Астрахань, 2012. – 16 с.

7. Уразбахтина Л.Р. Триадная форма представлений ключевых компетенций / Л.Р. Уразбахтина, И.Б. Герасимова, А.Г. Карамзина // Проблемы качества образования : материалы Всероссийской XXII научно-методической конференции. – Уфа; Москва, 2012. – С. 225-228.

Профессиональная подготовка студентов в настоящее время производится на основании Федеральных государственных образовательных стандартов высшего профессионального образования третьего поколения (в частности – ФГОС ВПО III+), определяющих требования к результатам освоения основных образовательных программ (ООП) подготовки в терминах компетентностного подхода. В основе этих изменений лежит идея о переходе к оценке уровня подготовки выпускника высшего учебного заведения (ВУЗа) в форме измерения компетенций. Экономические и социальные перемены в современном российском обществе выдвигают принципиально новые требования к профессиональной квалификации выпускников. Все это предопределяет необходимость разработки методов оценивания уровня сформированности профессиональных компетенций студентов, необходимых для последующего мониторинга учебного процесса в ВУЗе и может служить основой для управленческих решений.

Теоретический анализ. На основании анализа научной литературы относительно существующих подходов к оценке профессиональных компетенций выявлены; основные принципы построения математической модели и системы оценивания результатов обучения; многокомпонентность содержания понятия «профессиональной компетенции», ее междисциплинарный характер, способы и дидактические средства формирования профессиональных компетенций; необходимость разработки математической модели оценивания уровня сформированности профессиональных компетенций с целью совершенствования качества образования с учетом требований нормативных документов и рынка труда. В основу работы было положено определение, где профессиональная компетенция рассматривается как интегральная оценка качества подготовленности выпускников, которая должна включать в себя не только оценку индивидуальных образовательных достижений, воплощенных в виде усвоенных студентом знаний и умений, но и оценку личностных профессионально-значимых сформированных мотивационных показателей, характеризующих готовность студента к реализации профессиональных функций [2-7].

Таким образом, модель оценивания профессиональных компетенций должна определяться как комплекс оцениваемых характеристик студента-выпускника, который содержит:

• множество оценок, полученных за дисциплины, сгруппированные по компонентам оценивания;
• множество оцениваемых результатов внеучебной деятельности студента;
• оценка его профессиональной мотивации к обучению и к будущей профессиональной деятельности.

Моделирование процесса оценивания профессиональных компетенций студентов-выпускников ВУЗа выполнялось в четыре этапа. На первом этапе необходимо сформировать компетентностную модель выпускника, для чего проводится анализ нормативной и информационной базы (ФГОСВПО, ООП, требования со стороны работодателей, общественных объединений и т.д.), где предопределяется эталонный уровень требований, предъявляемый для направления образовательной деятельности, и это составляет теоретическую основу математической модели оценивания профессиональных компетенций. На втором этапе выполняется сбор данных результатов учебных достижений студента за весь период обучения до текущего момента, а также результаты его творческой, интеллектуальной и научно-исследовательской и других видов деятельности, анализ коэффициентов взаимосвязи дисциплин в рамках компетентностно-ориентированной образовательной программы. Третий этап заключается в обработке полученных результатов, вычислении составляющих для математической модели оценивания профессиональных компетенций и её построение. На четвертом этапе выполняется проверка адекватности и качества модели с помощью соответствующего инструмента, анализ и визуализация полученных данных, рекомендации по корректировке процесса формирования компетенций.

Таким образом, задача оценивания профессиональных компетенций студента-выпускника сводится к поэтапному представлению результатов учебной и других видов деятельности. Разработанная математическая модель оценивания результатов обучения в виде оценок профессиональных компетенций описывается тремя определяющими величинами, это: покомпонентная оценка учебных достижений студента , оценка личностных характеристик студента , оценка профессиональной мотивации студента ; и одной определяемой, это: оценка профессиональной компетенции , где – количество профессиональных компетенций, – учебный период (аттестация, семестр, учебный год и т.д.):

Требуется определить функциональную зависимость между рассматриваемыми величинами, характеризующими оценку профессиональных компетенций.

Метод моделирования. Для решения поставленной задачи был использован подход «условного» моделирования – условное подобие, который заключается в замещении модели-оригинала по определенной договоренности, приписанной этой модели, «условной» моделью, в основе которой лежит теория подобия и анализ размерностей [1].

Рассмотрим систему и физическую систему , при этом .

И пусть – основные единицы измерения системы (размерности величин рассматриваемой системы) и , тогда:

(1)

где .

Проведем соответствие между системами и такое, что .Пусть , , …, .

Согласно π-теореме:

(2)

где .

Для выполнения условия (2) необходимо, чтобы физические величины являлись первичными величинами. В качестве первичных величин выбирают те величины, размерности которых являются независимыми функциями, т.е. при любых ,,..., справедливо выражение:

(3)

Пусть и выполняется условие (3), тогда формула (2) примет вид:

(4)

Перепишем формулу (4) с учетом условия (1):

(5)

Приравняем показатели степеней левой и правой частей уравнения (5) при одинаковых основаниях, получим систему:

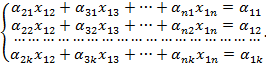
Найдем , решив систему любым известным и удобным способом. Таким образом, получив показатели переменных для системы , имеем возможность записать аналитическое выражение функции от переменных , выполним обратный переход от системы к системе :

Аналогично, рассмотрев все комбинации соответствия , получим множество всех решений для записи функциональной зависимости от :

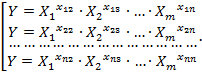
Экспериментальная часть. Ранее установлено, что математическая многокомпонентная модель оценивания профессиональных компетенций представлена как система всесторонних оценок образовательной деятельности студента-выпускника ВУЗа. На основе принятой идеальной физической модели требуется установить зависимость между результатом оценивания профессиональных компетенций и системой показателей этих оценок. Сравним систему оценивания профессиональных компетенций с механической системой , в которой любая физическая величина имеет размерность, выраженная в виде монома от основных величин:

(6)

где М – размерность массы, L – размерность длины, Т – размерность времени, . Выбор основных размерных величин, через которые выражаются все остальные, это вопрос соглашения экспертов. Размерности других физических величин механической системы напрямую связаны с их определением и, как следствие, со способами их измерения.

Пусть , что соответствует физической величине «сила», – «работа», – «ускорение», – «скорость» и (таблица 1). Так как , , ,, то с учетом формулы (6) получим комплекс выражений:

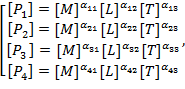
или

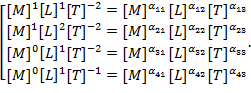
Проверим, могут ли физические величины для выбранной нами системы являться первичными, для этого вычислим определитель, составленный из показателей правой части уравнений системы:

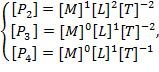
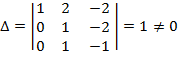
Так как , то величинымогут быть определены как первичные, и размерности соответствующих величин являются независимыми функциями от , тогда, применительно к механической системе, уравнение (2) примет вид:

(7)

отсюда получим:

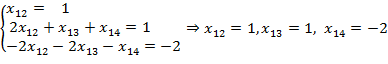(8)

С учетом найденных показателей (8) выполним перевод уравнения (7) к параметрам системы модели-оригинала и получим аналитическое выражение модели-оригинала оценивания профессиональных компетенций:

Аналогично, рассматривая случаи, когда оценка профессиональной компетенции соответствует физическим величинам, характеризующим работу и другие варианты замены, получим результаты вычислений, которые отражены в таблице 1.

Таблица 1

Сводная таблица вариаций «размерной» модели

Таким образом, получены четыре типа функциональной модели для оценки профессиональных компетенций. Возникает проблема выбора модели, которая наилучшим образом отражает результаты оценивания профессиональных компетенций. Разрешить данный вопрос позволит применение множественного корреляционно-регрессионного анализа на основе вычислительного эксперимента.

Предложенная методика оценивания профессиональных компетенций апробирована в ходе эксперимента, в котором оценивался уровень сформированности профессиональных компетенций у студентов-выпускников направления 230100 – Информатика и вычислительная техника за весь период обучения на момент окончания ВУЗа. Для проведения статистического исследования в качестве эмпирической базы на этапе предварительной подготовки были использованы исходные данные учебной, научно-исследовательской и творческой деятельности студентов с I по IV курс обучения контрольной группы, представленные учебно-методическим отделом, а также результаты экспертных опросов. В качестве экспертов выступили потенциальные работодатели, профессорско-преподавательский состав, выпускники и студенты ВУЗа. Все вычислительные операции были выполнены с использованием программ статистической обработки информации: SPSS 21, MS Excel, ПК Эксперт (программный комплекс экспертного оценивания методом парного сравнения).

Итак, по результатам множественного корреляционно-регрессионного анализа (таблица 2) и теоретико-логическим заключениям наиболее адекватной, в случае поставленного эксперимента, признается математическая модель оценивания профессиональных компетенций № 4 (таблица 1):

Таблица 2

Обобщенные результаты корреляционно-регрессионного анализа

Результаты численного эксперимента подтвердили, что применение разработанного метода обеспечивает получение адекватной математической модели, способной провести объективное и достоверное оценивание профессиональных компетенций выпускников ВУЗа.

Вывод. Таким образом, для решения поставленной задачи, а именно: вывод обобщённых расчетных зависимостей параметров математической модели процесса оценивания профессиональных компетенций может быть применен новый оригинальный подход, основанный на теории подобия и анализа размерностей. Проведённые вычислительные эксперименты подтвердили достоверность результатов, адекватность и эффективность разработанных моделей и алгоритмов оценивания профессиональных компетенций, позволили определить наиболее статистически значимую модель.

Рецензенты:

Аксёнов Б.Г., д.ф.-м.н., профессор, заведующий кафедрой математики, ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет», г. Тюмень;

Мальцева Т.В., д.ф.-м.н., профессор, проректор по научной и инновационной работе, ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет», г. Тюмень.

Библиографическая ссылка