При разработке комплексов для подготовки оператора транспортных человеко-машинных систем одной из актуальных задач является определение характеристик внутренних помех и их локализации [2; 4; 6-8]. Рассмотрим нестационарную систему, замкнутую обратной связью и имеющую внутреннюю помеху (рис. 1).
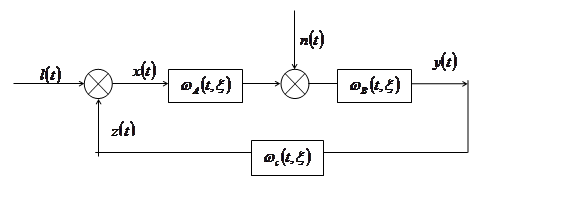
Рис. 1. Замкнутая система с помехой.
В режиме функционирования производятся измерения 
и
; можно считать известными математические ожидания 
и корреляционные функции 
, 
. Пусть далее известны:
- импульсная переходная функция всей системы 
;
- импульсная переходная функция 
части объекта регулирования, где действием помех можно пренебречь;
- импульсная переходная функция 
объекта по отношению к помехе;
- импульсная переходная функция 
обратной связи.
Требуется определить статистические характеристики помехи 
, 
. Можно показать, что для стационарных систем, если помеху 
привести к выходу системы (
), то среднее значение стационарной помехи, приведенной к выходу
,
.
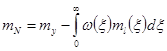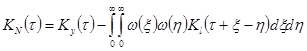В случае необходимости могут быть найдены спектральные характеристики приведенной помехи. В частности, спектральная плотность 
вычисляется по формуле:
,
где 
- частотная характеристика системы, соответствующая импульсной переходной функции 
.
При приведении помехи к выходу рассматриваемую структурную схему можно изобразить в виде, приведенном на рис. 2.
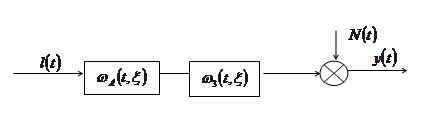
Рис. 2. Преобразованная структурная схема.
Справедливо
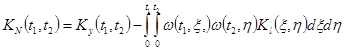
(знания , , для отыскания корреляционной функции помехи, приведенной к выходу системы, не требуется).
Часто знания статистических характеристик приведенной помехи может оказаться недостаточным, и необходимо выявить место ее возникновения, то есть возникает задача структурной локализации помехи. В общем случае задача сводится к отысканию импульсных переходных функций и звеньев системы. А именно, требуется определить такую функцию части функционирующей системы, которая максимально подавляет помеху, а также функцию , которая, наоборот, максимально пропускает ее. В связи с этим структурную локализацию помехи целесообразно производить последовательным переносом 
через звенья 
системы против хода сигнала ошибки, определяя характеристики помехи в каждой узловой точке структурной схемы исследуемой системы. Необходимо исходить из априорных данных о системе, задаваясь импульсными переходными функциями 
, ее звеньев, сохраняя условия:
,
.
Определим статистические характеристики помехи в узловой точке структурной схемы (рис. 3).
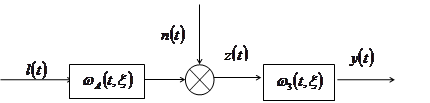
Рис. 3. К определению статистических характеристик помехи.
Для системы с постоянными параметрами, внутренние помехи в которых стационарны, можно записать выражение, справедливое для установившегося режима:
,
,
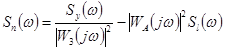- спектральная плотность помехи.
Рассмотрим приложение указанных методик к разработке авиационных тренажеров [1; 3; 5; 9; 10]. Примем:
- передаточные функции
,
;
- статистические характеристики возмущения
,
;
- статистические характеристики выходной координаты
, 
.
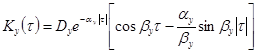Предполагалась справедливость гипотезы о некоррелированности внутренней помехи и входного сигнала системы (входной сигнал (или возмущение) регистрируется).
Требуется найти статистические характеристики .
Схему на рис. 1 преобразуем в схему на рис. 3. При 
получим
,
где
, 
,
, 
,
,
,
,
,
.
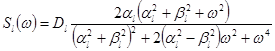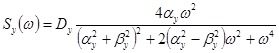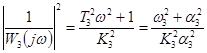Спектральная плотность помехи определится в виде
.
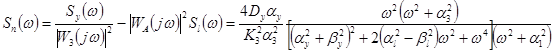Таким образом, получили нижеприводимый алгоритм для определения характеристик помехи.
1. Из уравнения динамики определяются передаточные функции
,
, 
.
2. Определяется спектральная плотность помехи
,
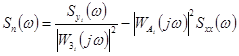изменяя узловые точки.
Замечания. 
и 
определяются по уравнениям движения; 
, 
аппроксимируются аналитическими выражениями.
Рецензенты:
Родионов Ю.В., д.т.н., профессор, декан автомобильно-дорожного института ПГУАС, заведующий кафедрой «Эксплуатация автомобильного транспорта», г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры «Информационно-вычислительные системы» Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Дулатов Р.Л. ИДЕНТИФИКАЦИЯ ПОМЕХ, НЕ КОРРЕЛИРОВАННЫХ С ВХОДНЫМ СИГНАЛОМ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17837 (дата обращения: 15.10.2024).