Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Терентьев А.В. 1

---

1 ФГБОУ ВПО «Санкт-Петербургский Государственный морской технический университет»

Проводится аналитический и численный анализ статического поведения стержня трубчатого поперечного сечения, потерявшего устойчивость. Переменное вдоль длины стержня поперечное сечение имеет постоянный внутренний и переменный внешний диаметры. При помощи варьирования функционала энергии получено нелинейное дифференциальное уравнение, определяющее равновесное положение стержня для случаев нагружения его сжимающей силой и изгибающими моментами. Рассмотрены случаи статического изгиба с большой амплитудой, вызванные действием осевой сжимающей силы и заданными изгибными деформациями в определенных поперечных сечениях. Для определения статического положения стержня используется метод локальных вариаций. Получены формы равновесия стержня при значительных изгибных деформациях. Произведено сравнение точного аналитического решения с численным решением для симметричной формы равновесия стержня. Выявлено хорошее соответствие между аналитически и численными решениями, подтверждающее правильность использования алгоритма.

Статья в формате PDF

125 KB

переменное поперечное сечение

метод локальных вариаций

сжимающая посткритическая сила

изгибные деформации

1. Баничук Н.В., Черноусько Ф.Л. Вариационные задачи механики и управления. — М.: Наука. 1973. — 240 с.

2. Павленко Ю.Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392с.

3. Работнов Ю.Н. Механика деформируемого твердого тела. — М.: Наука, 1988. — 712 с.

4. Lagoudas D.C., Tadjbaksh I.G. Active flexible rods with embedded SMA fibers// Smart Materials and Structures . – 1992. Vol.1 – p. 162–167

5. Yalcintas M., Coulter J.P., Don D.P. Structural modeling and optimal control of electroreological material based adaptive beams// Smart Materials and Structures. – 1995. p. 207–214

Постановка задачи

Цель данной работы заключалась в проведении анализа посткритического поведения сильно деформированного стержня [5]. Рассмотрен стержень трубчатого поперечного сечения, имеющий переменный осевой момент инерции:

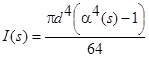, (1)

где , — внешний переменный диаметр по длине стержня, — внутренний диаметр поперечного сечения. Единственное ограничение, накладываемое на функцию , следует из физического смысла задачи:

(2)

Далее выбираем функцию в следующем виде:

, (3)

где с — некоторые константы.

Задание функции в виде (3) обеспечивает довольно гладкую симметричную зависимость момента инерции от осевой координаты. Например, если , то толщина стержня стремится к нулю по ее концам. Внешний диаметр посередине стержня превышает на 10% внутренний диаметр, который постоянен по его длине.

Положение равновесия стержня определяется углом , определяемым между горизонталью и касательной к изогнутой оси стержня (см. рис. 1 для случая сжатия осевой силой), выбранном в виде неизвестной функции. Данный угол является функцией материальной координаты .

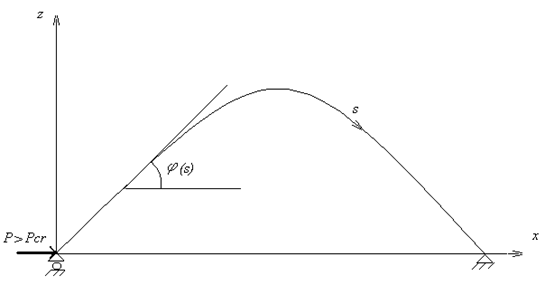
Рис. 1. Сильно изогнутый стержень под действием сжимающей силы

Для того чтобы получить уравнения, определяющие статическое равновесие стержня, подвергнем минимизации следующий функционал потенциальной энергии [2]:

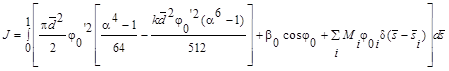(4)

Условие стационарности данного функционала определяет устойчивое положение равновесия стержня. Первое слагаемое в квадратных скобках представляет вклад линейной компоненты в потенциальную энергию, второе относится к нелинейной компоненте. Постановка задачи (4) учитывает нагружение и сжимающей силой, и изгибающими моментами. Данное выражение записано в безразмерной (разделено на множитель ). В (4): — безразмерная осевая координата, — значение безразмерной статической осевой сжимающей силы, — отношение внутреннего диаметра к длине стержня, — символ Кронекера и — изгибающий момент в точке .

Вариация функционала энергии (4) относительно неизвестной функции приводит к следующему дифференциальному уравнению:

(5)

Рассмотрим шарнирно-опертый стержень, при этом данное дифференциальное уравнение следует решать с кинематическим условием:

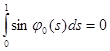, (6)

которое означает, что боковое перемещение стержня равно нулю на правом конце.

Решение для симметричной конфигурации стержня

Аналитического решения данной задачи для произвольной функции не существует, так что необходимо применить какой-то численный алгоритм. Используется алгоритм метода локальных вариаций [1], который ограничивается симметричной конфигурацией трубки, так что распределение изгибающих моментов должно быть симметрично при .

При задача имеет хорошо известное аналитическое решение для случая нагружения осевой сжимающей силой. Элементарный линейный анализ устойчивости дает величину статической силы потери устойчивости , а нелинейный анализ закритического поведения для > определяет положение трубки в виде эластики Эйлера [3]. Данный случай служит обычной задачей для проверки численного алгоритма.

В случае задания распределенных моментов вводим их осевыми деформациями , заданными на верхнем фибре трубки (т.е. на расстоянии от нейтральной оси) при заданном поперечном сечении [4]. Деформации на расстоянии от нейтральной оси должны быть такими же по величине и иметь противоположный знак. Изгибающий момент, действующий в данном поперечном сечении, определяется формулой (в размерном виде).

Метод локальных вариаций позволяет определить изгибающие моменты , действующие в данном поперечном сечении стержня, в виде:

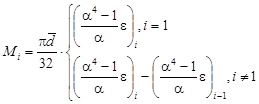(7)

где .

Если деформация задана только в точке , то сосредоточенный изгибающий момент вычисляется только в точке .

Для проверки численной процедуры произведено сравнение найденной формы стержня с имеющимися аналитическими результатами. Данный тест относится к равномерному распределению функции вдоль оси стержня. Параметры численной процедуры выбраны следующими: N=16..1024 — число интервалов по оси стержня, h =— шаг варьирования. Величина статической осевой силы . Если функция определяется по алгоритму метода локальных вариаций [1], то боковое перемещение и соответствующее горизонтальное перемещение находятся в виде:

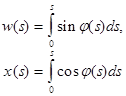(8)

На рисунке 2 представлены две формы равновесного положения стержня (точное решение и решение, полученное по методу локальных вариаций). Хорошее соответствие между двумя кривыми на рисунке 2 доказывает, что принятая численная процедура может быть использована для определения закритического статического положения стержня после потери устойчивости.

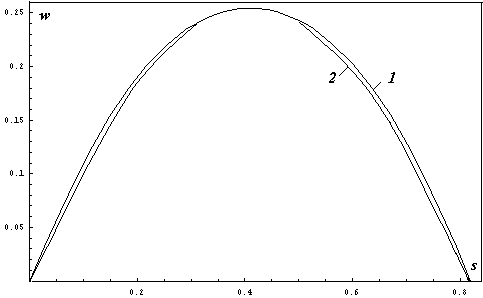
Рис. 2. (при , ) кривая 1 представляет закритическое положение стержня, соответствующее эластики Эйлера, найденной в форме эллиптических интегралов (точное решение), а кривая 2 определяет форму равновесия, полученную с помощью алгоритма метода локальных вариаций

На рисунке 3 показано положение равновесия, которое определяется двумя симметрично расположенными (,) сосредоточенными моментами (). Изгиб существует только между точками, где приложены моменты, внешние части стержня остаются прямыми.

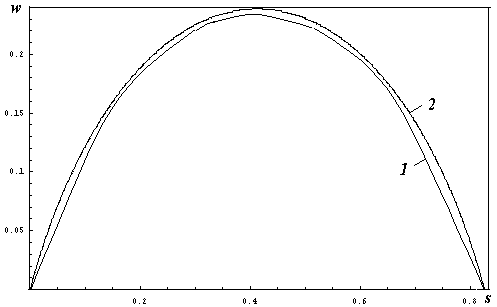
Рис. 3. (при , ) кривая 1 представляет точное решение, а кривая 2 определяет численное решение

Алгоритм решения нелинейной задачи статического изгиба определяет то, что положение равновесия должно быть симметричным.

Выводы

Произведен статический анализ шарнирно-опертого стержня. Для того чтобы получить решение, определяющее статическое положение стержня, был использован метод локальных вариаций. Сопоставление численного и аналитического решений позволило подтвердить правильность используемого алгоритма.

Рассмотренная система представляет некоторые особенности механических систем, используемых в практических приложениях, а именно в химической и нефтегазовой промышленности.

Рецензенты:

Картузов Е.И., д.т.н., профессор кафедры теоретической механики Санкт-Петербургского Государственного морского технического университета, г. Санкт-Петербург;

Сорокин С.В., д.т.н., профессор кафедры сопротивления материалов Санкт-Петербургского Государственного морского технического университета, г. Санкт-Петербург.

Библиографическая ссылка