Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Для математического моделирования процесса самообучения рассмотрена мотивация обучающегося для получения знаний по организационно-экономическому компоненту вектора знаний. Современные требования к конечному результату профессиональной подготовки в вузе – это подготовленный квалифицированный специалист, готовый применить полученные знания, умения и навыки на конкретном предприятии, в конкретной ситуации.В связи с переходом страны к рыночным отношениям и проводимыми реформами профессионально подготовленный выпускник среди прочих задач должен уметь решать вопросы экономики и управления [10].Практически во всех дисциплинах специальности рассматриваются организационно-экономические вопросы, присущие данному предмету. Профессиональная подготовка в вузе распределена как во времени, так и в пространстве и объединяет множество дисциплин, методик, моделей обучения [2], при этом особое значение приобретает познавательная деятельность обучающегося, определяемая мотивацией и позволяющая ему овладевать необходимыми знаниями[6].

Основные положения

Учебный процесс по подготовке профессионала в рамках методологии[1]рассматривается как целостная система управления образовательным процессом по единому интегрированному вектору знанийна всех стратах обучения. Учебный процесс распределён во времени, информация по отдельным дисциплинам передаётся в отдельные промежутки времени – занятия, что позволяет рассматривать учебный процесс как совокупность отдельных этапов, на которых особое значение приобретает управление познавательной деятельностью обучающегося посредством повышения его уровня самоорганизации и самообучения при непрерывном снижении степени явного участия преподавателя в управлении обучением[1,6,8].

С учётом факторов восприятия и забывания, структура математической модели познавательной деятельности обучающегося может быть представлена следующим образом  (рис. 1)[3,6]:

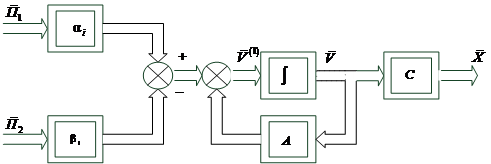
Рис. 1.Структура модели познавательной деятельности обучающегося

Коэффициенты  позволяют учесть интенсивность восприятия информации по каждому компоненту вектора знаний в каждом предмете,  – интенсивность и время обучения,  – интенсивность забывания информации по каждому компоненту в каждом предмете, – функция забывания , матрица – характеризует механизм и скорость усвоения знаний, – свёртка компонентов вектора знаний в единую оценку .

Каждый из группы обучающихся, усваивает только субъективную часть информации, обусловленную мотивацией и соответствующую его интересам, наклонностям, способностям, работоспособности, знаниям, умениям, трудолюбию, накопленному опыту, уровню подготовки[1,2,6].

Специфическая особенность обучающегося как преобразователя информации проявляется в том, что он не является пассивным приёмником, воспринимающим с помощью органов чувств информацию от окружающей среды, а активно взаимодействует с окружающей средой с целью получения требующейся ему информации и является инициатором такого взаимодействия.

С точки зрения управления процессом обучения функции самоуправления обучающимся можно выделить и распределить по уровням:– мотивация , – критерии оценки знаний ,– цели и задачи обучения ,– методология обучения ,– содержание предмета изученияи представить обучающегося как многоуровневую (многослойную) систему управления[3,4,5].

Математическую модель многоуровневой (многослойной) системы управления самообучением построим для организационно-экономического компонента() вектора знаний.

Нижний уровень управления – содержание предмета изучения:основные экономические вопросы и задачи управления производственными процессами,основные задачи проведения технико-экономических расчётов, критерии технико-экономической эффективности управления, технико-экономические расчёты по оценке технико-экономической эффективности отдельных агрегатов и систем в целом Анализ образовательного процесса в пространстве вектора знаний показывает, что организационно-экономический компонент присутствует во всех учебных дисциплинах.Cтруктура подготовки специалистов по направлению «Автоматизация технологических процессов и производств» по организационно-экономическому компоненту в пространстве состояний стратифицирована по предметам, изучаемым в каждом семестре, чтопозволяет получать непрерывные экономические знания и умение решать экономические вопросы при изучении дисциплин специальности на протяжении всего срока обучения [9,10].

Математическая модель нижнего уровня управления включает замкнутый контур самообучения и самоконтроля уровня знаний в соответствии с множеством состоянийпрогнозируемых результатов познавательной деятельности обучающихся по предметно-содержательной составляющей знания  (рис.2) [5,7,8,9].

Механизм управления с использованием интеллектуального оператора обучающегося  в нулевом слое описывается выражением

.

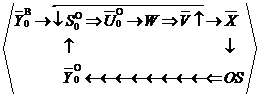Рис. 2. Диаграмма управления предметно-содержательной составляющей знаний

Переменные на приведенной диаграмме представлены векторами состояния , выхода , управления  и воздействия окружающей среды . Операторы преобразования переменных обозначены:  – интеллектуальный оператор управления;  – оператор, отражающий динамические процессы управления познавательной деятельностью;  – оператор, отражающий взаимосвязь обучающегося с окружающей средой. Двойные стрелки использованы для обозначения выходов операторов.

Динамическая часть, обозначенная , задаётся в пространстве состояний уравнениями:

Управление механизмом познавательной деятельности – первый уровень управления – совокупность методов, приёмов и способов познавательной деятельности, которыми владеет обучающийся – задаётся интеллектуальным оператором обучающегося  (рис.3).

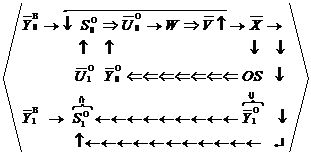
Рис. 3.Диаграмма управления механизмом познавательной деятельности

Большое значение здесь имеет общий уровень подготовки учащегося, желание приобретать знания и, конечно, влияние окружающей среды, которое может быть и положительным и отрицательным.

Изменение структуры и параметров внутреннего оператора  обеспечивает управляющее воздействие  с выхода оператора . Механизм управления  направлен на приспособление обучающегося к методологии обучения соответственно уровню знаний обучающегося. Как и в любой другой деятельности человека, огромное значение имеет контроль, который в данном случае осуществляется анализом полученных результатов. Это могут быть и оценки, полученные за выполненные задания, и, что очень важно, самооценка результатов. На основании анализа происходит переоценка, коррекция,вариация способов обучения и может быть определено выражением

Коррекция структуры и параметров управляющего интеллектуального оператора осуществляется управляющим воздействием .

 

Следующий уровень управления познавательной деятельностью обучающегося – формирование критериев оценки знаний. В соответствии с компетенциями, которыми должен обладать обучающийся, производится коррекция тем и содержания организационно-экономической составляющей в изучаемых предметах, коррекции подлежат и методы освоения знаниями [3,4,6,8]. Диаграмма этого уровня содержит три контура управления. Во внешнем контуре управления критериями оценки знаний находится интеллектуальный оператор , на выходе которого формируются два управляющих воздействия:  – управление предметно-содержательной компонентой обучения и  – управление методологией познавательной деятельности обучения[6].

Механизм интеллектуального управления  во втором слое описывается выражениями

,

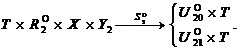
которые образуют математическую модель обучающегося как трёхслойную обучающуюся систему (рис. 4).

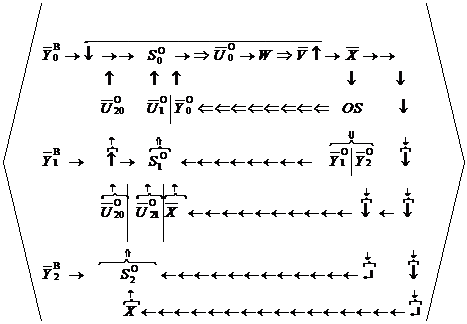
Рис. 4. Диаграмма управления критериями оценки знаний

Управление целями и задачами познавательной деятельности обучающегося может быть описано выражением

Здесь происходит синтез целей и задач управления познавательной деятельностью обучающегося – появляется четвёртый контур интеллектуального управления целями и задачами (рис. 5).

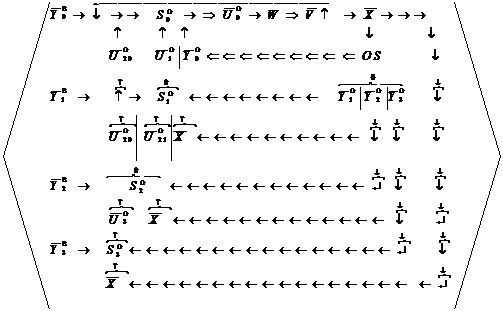
Рис. 5. Диаграмма управления целями и задачами

Математическая модель управляющей части обучающегося как четырёхслойной обучающейся системы включает в себя интеллектуальное управляющее воздействие , формируемое в четвёртом контуре, которое направлено на управление третьим контуром посредством воздействия на интеллектуальный оператор . Таким образом, математическая модель этого контура имеет вид:

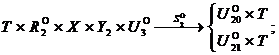
Основная задача пятого контура – управление мотивацией обучающегося – знание и умение решать организационно-экономические вопросы и применять эти знания на практике. Посредством множества управляющих воздействий , формируемых в пятом контуре интеллектуального управления, производится выбор целей и задач из множества вариантов интеллектуального управления (рис. 6).

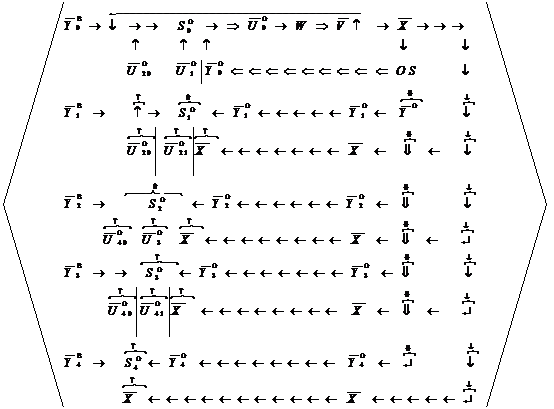
Рис. 6. Диаграмма управления мотивацией обучающегося

Математическая модель пятислойной структуры обучающегося с учётом его динамических особенностей описывается следующей системой выражений:

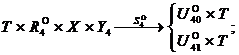
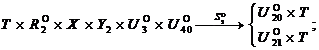
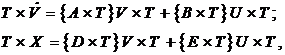
Выводы

Управляющая часть обучающегося как многослойная интеллектуальная система представляет собой целостную многослойно распределённую интеллектуально управляемую систему, а совокупность управляющих воздействий различных слоёв образует единый внутренний вектор управляющих воздействий [7,9].

Таким образом, многослойная математическая модель профессиональной самоподготовки обучающегося по организационно-экономическому компоненту вектора знаний образует вложенную структуру с подчинением каждого низшего уровня управления высшему.

Рецензенты:

Кошев А.Н., д.х.н., профессор кафедры «Информационно-вычислительные системы» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;

МачневВ.А.,д.т.н., профессор, профессор кафедры «Основы конструирования механизмов и машин» ФБГОУ ВПО «Пензенская государственная сельскохозяйственная академия», г. Пенза.