1
Гарькина И.А.
1
Данилов А.М.
1
Сорокин Д.С.
1
1 ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства»
Предлагается методика объективизации оценки оператором характеристик объекта в процессе нормального функционирования целостной человеко-машинной системы. Актуальность исследований определяется необходимостью получения требуемых имитационных характеристик тренажных и обучающих комплексов по подготовке операторов мобильных систем. Методика оценки основывается на специально разработанном функционале, позволяющем производить сравнение динамических характеристик двух систем: оператор – реальный объект и оператор - модель объекта. В функционале учитываются апериодичность или колебательность объекта, собственные частоты колебаний, безразмерные коэффициенты затухания, а также иные инварианты матрицы уравнений движения. C использованием функционала определены области равных оценок, позволяющие получить класс объекта при заданной балльности шкалы. Приводится практическая реализация методики.
Ключевые слова: эргатические системы
подготовка операторов
управляющие воздействия
связь с параметрами объекта
функционал качества
области равных оценок
классификация объектов
имитационные характеристики тренажеров.
1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э.В., д.т.н., проф. Данилова А.М. – Пенза: ИИЦ ПГУ. – 2005. – 146 с.
2. Будылина Е.А., Гарькина И.А., Данилов А.М. Приближенные методы декомпо-зиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. – 2013. – № 3. – С. 150-156.
3. Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов // Фундаментальные исследования. – 2014. – № 6 (часть 4). – С. 698-702.
4. Будылина Е.А., Данилов А.М., Пылайкин С.А., Лапшин Э.В. Тренажеры по подготовке операторов эргатических систем: состояние и перспективы // Современные проблемы науки и образования. – 2014. – № 4; URL: www.science-education.ru/118-13874.
5. Гарькина И.А., Данилов А.М. Аппроксимационные задачи при разработке ими-таторов транспортных систем: распараллеливание вычислительных процессов / Вест-ник Таджикского технического университета. –№ 4 (24). – 2013. –С.75-80.
6. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое и компьютерное мо-делирование сложных систем. – Пенза: ПГУАС. – 2011. – 296 с.
7. Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения систем-ных методологий, теорий идентификации и управления / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). – 2009. – № 2. – С. 77-81.
8. Гарькина И.А., Данилов А.М., Петренко В.О. Решение приближенных уравне-ний: декомпозиция пространственного движения управляемого объекта // Современные проблемы науки и образования. – 2014. – № 5; URL: www.science-education.ru/119-14766.
9. Гарькина И.А., Данилов А.М., Прошин И.А. Тренажеры модульной архитектуры для подготовки операторов транспортных систем / XXI век: итоги прошлого и проблемы настоящего (плюс) Серия: технические науки. Машиностроение и информационные технологии. - №12(16). – 2013. –С. 37-42.
10. Гарькина И.А, Данилов А.М., Пылайкин С.А. Транспортные эргатические си-стемы: информационные модели и управление / Мир транспорта и технологических машин. – №1(40). – 2013. – С.115-122.
11. Гарькина И.А., Данилов А.М., Пылайкин С.А. Тренажеры и имитаторы транс-портных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. – №3(42). – 2013. – С.115-121.
12. Данилов А.М., Гарькина И.А., Гарькин И.Н. Управление объектами на подвиж-ном основании: оптимизация конструктивной и структурной схем / Региональная архитектура и строительства. – 2014. - №3 (20). – С.102-108.
13. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ. – 2011. –№2. – С.18-23
14. Данилов А.М., Домке Э.Р., Гарькина И.А. Формализация оценки оператором характеристик объекта управления / Известия ОрелГТУ. Информационные системы и технологии. – 2012. – № 2 (70). – С.5-11.
15. Планирование эксперимента. Обработка опытных данных: монография / И.А.Гарькина [и др.]; под ред. проф. А.М.Данилова. – М.: Палеотип. – 2005. – 272 с.
Известно, стиль управления оператора эргатической системы, описываемой уравнением движения
(
, 
- вектор управления, 
- возмущающие воздействия), определяется собственными частотами колебаний и коэффициентами демпфирования объекта [10…15]. Поэтому актуальна объективизация оценки оператором управляемости объекта в процессе нормального функционирования целостной человеко-машинной системы [1…9]. Для классификации объектов воспользуемся функционалом
|
 , 
|
(1)
|
- корни характеристического полинома; 
- положительные весовые константы, 
- класс объекта в заданной N-балльной шкале.
В частности, для систем второго порядка области равных оценок на плоскости 
определятся в виде:
для колебательных систем относительно инвариантов
(
- след матрицы 
, 
=
; 
, 
(устойчивость), 
(колебательность), для рассматриваемых систем 
).
Из 
следует:
или
.
При фиксированном 
справедливо:
,
),
Так как 
и 
, то из выражений для 
и двойного неравенства 
получим:
.
Таким образом, области 
на плоскости 
определятся системой неравенств:
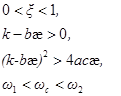
а области 
соотношениями
.
Здесь 
-множество на плоскости 
определяемое системой неравенств
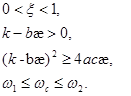
Для описания множеств и областей изучим поведение 
и 
как функций двух переменных k и .
Меньший корень 
уравнения
соответствует большему корню 
и возрастает с возрастанием k (непосредственно следует из уравнения и соотношения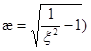 
.
Справедливо
;
.
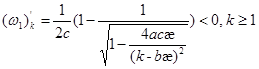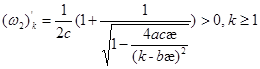Откуда следует 
.
Из выражений для 
и установленного выше неравенства 
следует
при 
.
При =0 (
имеем:
Нижняя граница области возрастает с возрастанием (убывает с возрастанием 
):
.
.
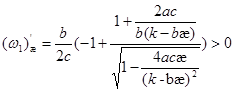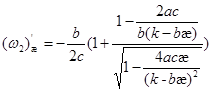Если для функционала 
, то при малых и при таких, что 
(то есть при , близких к 1) справедливо 
, и верхняя граница возрастает по (убывает по ) при , близких к нулю (при , близких к 1); при , близких к корню (при , близких к корню 
) имеет место 
.
Области (соответственно ) представлены на рис.1.
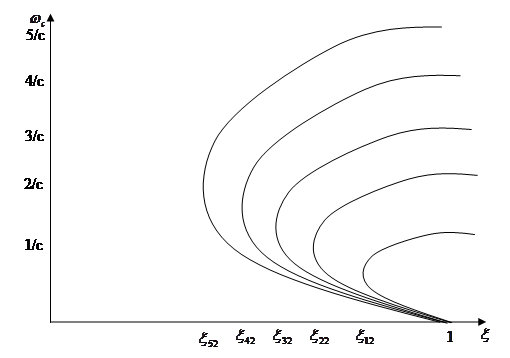
Рис.1. Области
Рассмотрим далее неколебательные системы (
).
Прежде всего отметим, для каждой из компонент 
справедливо
,
,
,
так что
,
, 
, 
.
Определим области равных оценок относительно инвариантов и 
.
Подставляя в 
и 
значения и через и 
, получим
; 
.
Откуда
|
|
(2)
|
|
|
(3)
|
Для неравенства (3) в силу 
дискриминант
.
Поэтому (3) выполняется при
|
 ,
|
(4)
|
|
 ,
|
(5)
|
то есть вне отрезка 
, где 
- корни трехчлена
,
, 
.
Отметим
для всех 
.
Действительно, если бы было
,
то из этого следовало бы
.
Так как 
, то
, 
, 
.
Полученное противоречие свидетельствует о справедливости (5) для всех .
Поэтому неравенства (2) и (4) несовместимы.
С другой стороны при всех
,
так как
при всех в силу
.
Таким образом, область решения системы неравенств (2) и (4) совпадает с областью решения неравенства (4). Поэтому для построения областей равных оценок достаточно построить лишь кривые
;
при 
(области равных оценок приводятся на рис.2).
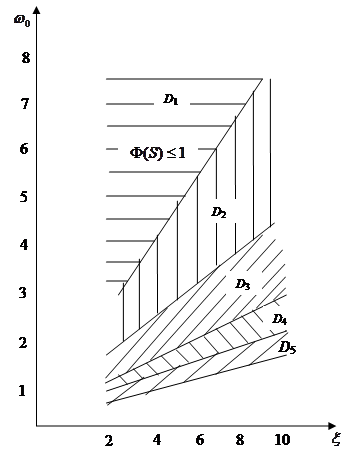
Рис.2. Аппроксимация областей равных оценок
Полученная методика многократно использовалась для оценки психофизиологической напряженности человека-оператора при управлении объектом, а также для оценки имитационных характеристик тренажных и обучающих комплексов, используемых для подготовки операторов транспортных систем [1…3,14].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, директор автомобильно-дорожного института ПГУАС, профессор кафедры «Эксплуатация автомобильного транспорта», г. Пенза;
Кошев А.Н., д.х.н., профессор, профессор кафедры информационно-вычислительных систем Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Сорокин Д.С. КЛАССИФИКАЦИЯ ОБЪЕКТОВ ЭРГАТИЧЕСКИХ СИСТЕМ ПО ИХ ДИНАМИЧЕСКИМ ХАРАКТЕРИСТИКАМ // Современные проблемы науки и образования. – 2014. – № 6.
;
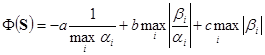URL: https://science-education.ru/ru/article/view?id=16136 (дата обращения: 20.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
