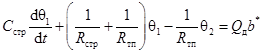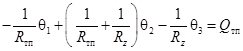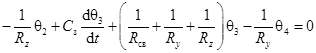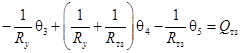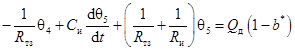Среди материалов, применяемых в качестве теплозащитных покрытий, резиновые смеси на основе каучука занимают особое место благодаря совокупности присущих им физико-механических и теплозащитных свойств [4] При этом наиболее эффективным способом достижения требуемого качества поверхности покрытий является абразивная обработка после каландрования и вулканизации. Шлифование резинового покрытия вызывает значительные механические и тепловые нагрузки в зоне контакта инструмента и обрабатываемого материала. Превышение допустимых значений этих нагрузок приводит к трещинам и прижогам на обработанных поверхностях, к выгоранию связки абразивного круга, затуплению и повышенному износу зерен, что в целом снижет производительность и качество обработки [5].
Цель работы
Целью физического моделирования параметров тепловых сопротивлений электросиловой схемы замещения процесса шлифования являлось установление закономерностей, отражающих влияние режимов шлифования на качество обработанной поверхности резиновых теплозащитных покрытий.
Материалы и методы исследования
Для определения температурносиловых параметров при абразивной обработке теплозащитных покрытий предложена электротепловая математическая модель и методика расчета параметров тепловых процессов. Для построения математической модели использован метод электрических аналогий, предполагающий представление технологических и тепловых подсистем в виде эквивалентных электрических цепей [1].
Составляющие силы резания при шлифовании по осям y, z имеют вид [3]:
|
Py = Pзy np B
Pz = Pзz np B |
(1) |
где ![]() Pзy , Pзz - радиальная и тангенциальная составляющие силы резания при микрорезании единичным зерном,Н; np - средневероятное число зерен, участвующих в резании на единице площади контакта круга с заготовкой, 1/мм2; В – ширина контакта в круге с заготовкой, мм;
Pзy , Pзz - радиальная и тангенциальная составляющие силы резания при микрорезании единичным зерном,Н; np - средневероятное число зерен, участвующих в резании на единице площади контакта круга с заготовкой, 1/мм2; В – ширина контакта в круге с заготовкой, мм; ![]() – длина контакта круга с заготовкой, мм.
– длина контакта круга с заготовкой, мм.
Силы резания при микрорезании единичным зерном определяются следующим образом:
|
|
(2) |
|
|
где β – угол между равнодействующей силой резания и скоростью резания (β = 34°); β1 – угол сдвига при резании; а – толщина среза зерна, мм; τ – среднее касательное напряжение в плоскости сдвига, МПа; bz – ширина среза зерна, мм; m – коэффициент трения стружки о поверхность зерна, (m = 0,46).
Для расчета угла сдвига β1 использовалась следующая зависимость:
|
|
(3) |
где g – передний угол резца (зерна), g = -45°; k – коэффициент продольной усадки стружки, k=2.
Средневероятное число зерен, участвующих в резании на единице площади контакта круга с заготовкой, определяется выражением:
|
|
(4) |
где cср – средневероятный размер зерна в круге, мм (c= 0,5-0,63); w* – скорость погружения зерен в обрабатываемый материал, мм/с; K* – концентрация режущего материала в круге, %;
v – скорость резания при шлифовании (v = 4,52 м/с); e – относительная критическая глубина заделки зерен в поверхностном слое круга (e=0,7…0,8).
Выражение для расчетной скорости погружения w*, характеризующей удельную производительность процесса обработки, при шлифовании периферией круга имеет вид:
|
|
(5) |
где vg – окружная скорость заготовки при круглом шлифовании, мм/с; t – глубина резания, мм; D – диаметр круга, мм.
Длина контакта шлифовального круга с заготовкой в формуле (1) определяется для внутреннего шлифования следующим образом:
|
|
(6) |
где d – диаметр заготовки, мм.
Тепловая мощность источников тепла, возникающих пи абразивной обработке теплозащитных покрытий, определяется на основе теплофизического анализа процесса шлифования. Общая тепловая мощность процесса шлифования распределяется между отдельными источниками тепловыделения в зоне контакта зерна с обрабатываемым материалом.
На рис. 1 представлена схема движения тепловых потоков, используемая в качестве основы при моделировании тепловых процессов при шлифовании теплозащитных покрытий.
В зоне абразивной обработки возникают три источника теплоты. Теплота деформации Qд, возникающая в области плоскости сдвига обрабатываемого материала, распределяется между стружкой Qдb* и изделием Qд (1-b*). При относительном движении стружки и абразивного зерна возникает теплота в результате трения по передней и задней поверхности режущего зерна Qтп и Qтз соответственно. Теплота от каждого источника распределяется между всеми телами, участвующими в процессе. Без потери точности и без отклонения от реальной физики процесса в целях упрощения математического описания введем понятие итоговых потоков теплообмена через контактные поверхности режущего выступа абразивного зерна. Итоговый тепловой поток между стружкой и передней поверхностью режущего зерна на площадке контакта обозначим Qп, а между обрабатываемым материалом и задней поверхностью зерна – Qз.
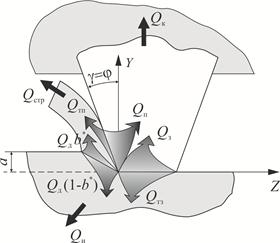
Рис. 1. Схема движения тепловых потоков при шлифовании
Qстр представляет тепловой поток, уходящий с движущейся стружкой. Тепловой поток Qи возникает в результате отвода тепла внутрь изделия в процессе его вращения. И, наконец, Qк характеризует теплоотвод в режущее зерно и связку шлифовального круга.
Обозначим через Q общую тепловую мощность процесса резания, приходящуюся на одно зерно. Тогда в соответствии с рис. 1 уравнения теплового баланса в зоне абразивной обработки будут иметь вид:
|
Q = Qстр + Qи + Qк =
Qстр = Qд
Qи = Qд (1 - Qк = Qп + Qз |
(7) |
Мощность источника теплоты деформации Qд [Вт] определяется следующим образом:
|
|
(8) |
PZO , PNO – совокупные средневероятные силы, действующие на режущие зерна.
|
|
(9) |
где m2 – коэффициент трения зерен с заготовкой по задней поверхности зерна (m2= 0,46); mz и my – коэффициенты, учитывающие распределение сил шлифования между зерном и связкой (mz = 0,95; my = 0,90); l2 – длина контакта зерна с обрабатываемым материалом по задней поверхности.
Нормальная составляющая силы резания PN может быть представлена в виде:
![]() .
.
Длина контакта зерна с покрытием по задней поверхности определяется выражением:
|
|
(10) |
где c – коэффициент затупления зерна (c=0,2–0,3 для острого круга, c=0,5 для затупившегося круга).
Коэффициент перераспределения тепла в стружку может быть представлен следующим образом:
|
|
(11) |
где w – коэффициент температуропроводности, м2/с.
Мощность источника тепла от трения стружки по передней поверхности зерна Qтп [Вт] может быть представлена следующим образом:
|
|
(12) |
Мощность источника тепла от трения заготовки по задней поверхности:
|
|
(13) |
Для построения математической модели процесса абразивной обработки с учетом тепловых и упругих систем использовался метод электрической аналогии [2], позволяющий описать тепловые и механические процессы. Фрагмент замещающей или эквивалентной схемы, отражающей динамику упругих и тепловых процессов в зоне абразивной обработки, представлен на рис. 2. Потенциалы в узловых точках эквивалентной системы отражают средние температуры характерных элементов исходной системы.
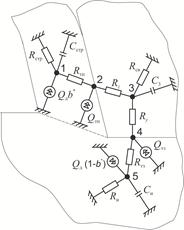
Рис. 2. Электротепловая схема замещения зоны контактного взаимодействия в процессе абразивной обработки
Тепловое сопротивление между стружкой и передней поверхностью зёрен Rтп [ºС/Вт] может быть представлено в следующем виде:
|
|
(14) |
где lм – коэффициент теплопроводности обрабатываемого материала, Вт/(м∙ºС); l1 – длина контакта стружки с передней поверхностью, мм.
Тепловое сопротивление между изделием и задней поверхностью зерен:
|
|
(15) |
Тепловое сопротивление стружки (отвод тепла со стружкой):
|
|
(16) |
Сопротивление отводу тепла в заготовку:
|
|
(17) |
Тепловое сопротивление потоку тепла в зерно со стороны стружки:
|
|
(18) |
где lз – коэффициент теплопроводности материала зерна; Lc»1.
Тепловое сопротивление потоку тепла в зерно со стороны заготовки:
|
|
(19) |
|
где |
|
Тепловое сопротивление отводу тепла от зерна в связку круга
|
|
(20) |
где lk – теплопроводность контакта зерна и связки.
Емкостные элементы Cи, Cз, Cстр [Дж/ºС] (рис. 2), учитывающие теплоемкость изделия, зерен шлифовального круга и стружки, определялись из выражений:
|
Ci = ci ρi Vi , |
(21) |
где ci – удельная теплоемкость соответствующих участков зоны обработки, [Дж/ (кг/ºС)]; ρi – плотность материалов, кг/м3; Vi – объемы изделия, зерен шлифовального круга и стружки в зоне обработки, м3.
Математическая модель, полученная по эквивалентной схеме методом узловых потенциалов, будет иметь следующий вид:
|
|
(22) |
|
|
|
|
|
|
|
|
|
|
|
где θi – средние температуры в узловых точках эквивалентной системы.
Результаты исследования и их обсуждение
Для оценки применимости представленной модели были выполнены расчеты силы резания при шлифовании и температуры в области контактного взаимодействия абразивного инструмента и обрабатываемого изделия при различных режимах обработки. В качестве примера на рис. 3 представлены отдельные результаты расчета, выполненные на основе представленной в работе математической модели.
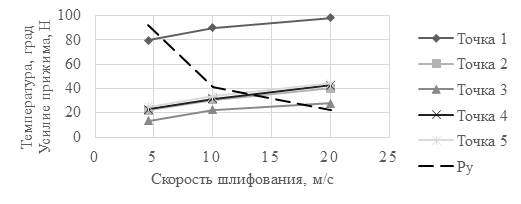
Рис. 3. Зависимость усилия прижима Py шлифовального круга и температуры в характерных точках 1-5 зоны резания от скорости шлифования
Экспериментальные исследования силовых и температурных характеристик процесса шлифования теплозащитного покрытия проводились в производственных условиях на модернизированном токарно-винторезном станке модели 166. При проведении экспериментов использовался абразивный круг 1-180х20х32 25AF36OBF 30 м/с. Исследования проводились на изделиях, подлежащих препорации для проверки адгезии покрытия согласно технологической инструкции контроля качества покрытия.
Результаты экспериментов подтвердили достоверность расчетов силовых и температурных характеристик процесса шлифования теплозащитных резиновых покрытий, максимальная относительная погрешность составила по усилию прижатия – 15%, по значениям температуры в зоне обработки – 12%.
Выводы
Приведена методика определения тепловых сопротивлений математической модели абразивной обработки теплозащитного покрытия, входящих в систему уравнений для расчета температуры и усилия прижатия шлифовального круга к изделию в зоне контакта. Использование метода электротепловой аналогии и метода узловых потенциалов позволяет встраивать приведенную модель в более сложные системы в качестве составной части для построения математической модели процесса шлифования с учетом динамического поведения технологического оборудования и комплексного воздействия тепловых и упругих процессов.
Исследования выполнены при финансовой поддержке Министерства образования и науки по гос. заданию (базовая часть) №2014/152, НИР №1460
Рецензенты:
Симонов Ю.Н., д.т.н., профессор, зав. кафедрой МТО ФГБОУ «ПНИПУ», Пермский национальный исследовательский политехнический университет, г. Пермь.
Щицын Ю.Д., д.т.н., профессор, зав. кафедрой СП и ТКМ ФГБОУ «ПНИПУ», Пермский национальный исследовательский политехнический университет, г. Пермь.
Библиографическая ссылка
Никитин С.П., Ханов А.М., Сиротенко Л. Д., Трофимов Е.О., Матыгуллина Е.В. РАСЧЕТ ТЕПЛОВОГО СОПРОТИВЛЕНИЯ ЭЛЕМЕНТОВ ЗОНЫ РЕЗАНИЯ ПРИ ШЛИФОВАНИИ ТЕПЛОЗАЩИТНЫХ ПОКРЫТИЙ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15981 (дата обращения: 23.02.2026).




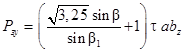
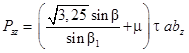
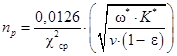 ,
,
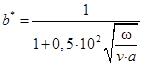 ,
,
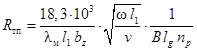 ,
,
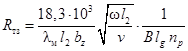 .
.
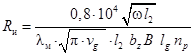 .
.
 ,
,
 ,
,
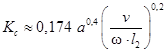 .
.