В последнее время в энергосистемах активно внедряется концепция гибких систем передачи переменного тока (FACTS). Данная концепция предполагает широкое применение регулируемых компенсирующих устройств, в том числе устройств продольной компенсации. Однако, применение таких устройств может приводить к возникновению колебаний на подсинхронных частотах вращения турбогенераторов – электромеханическому резонансу.
Часто при исследовании электромеханического резонанса (ЭМР) в энергосистемах пренебрегают действием насыщения стали ротора и статора синхронных машин [1, 5]. Это делается для упрощения процесса моделирования. В данной работе выполняется бифуркационный анализ математической модели энергосистемы. В этой математической модели учитывается насыщение, но пренебрегается АРВ и управлением турбиной. Учет насыщения в осях q и d приводит к повышению точности модели.
При учете насыщения стали в исследовании устойчивости принимают следующие допущения:
1) Поток рассеяния существует только в воздушном зазоре по пути основного магнитного потока. Следовательно, он не сильно влияет на насыщение стального сердечника. Таким образом, индуктивности рассеяния не зависят от насыщения стали. В результате насыщаются лишь взаимные потоки рассеяния ψmq и ψmd.
2) Потоки рассеяния обычно небольшие и их путь совпадает с основным магнитным потоком. Таким образом, насыщение может быть определено только через поток в воздушном зазоре.
3) Отношение насыщения между потоком в воздушном зазоре и магнитодвижущей силой (МДС) под нагрузкой такое же, как и без нагрузки. Это позволяет представлять характеристики насыщения через кривую насыщения холостого хода.
При исследовании используются современные методы нелинейной динамики для анализа действия (влияния) насыщения машины на ЭМР в реальной модели энергосистемы.
Рассмотрим энергосистему турбина – генератор – шина бесконечной мощности, представленную на рисунке 1. Модель и параметры выбраны для нагруженного генератора.
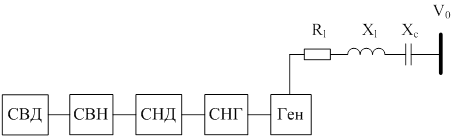
Рис.1 Схема системы турбина – генератор – компенсированная нагрузка. Механическая система (турбина) состоит из: ступени высокого (СВД), ступени низкого (СНД) давления, связей между ступенями (СВН и СНГ) и генератора (Ген)
Чтобы получить аналитические формулы потокосцеплений ψmd и ψmq в функции токов, представляем данные опытов, изображенные на рисунке 2, по следующим полиномам третьего порядка:
![]()
![]()
В которых dn и qn – постоянные. Очевидно, что взаимные потокосцепления рассеяния ψmd и ψmq – нелинейные функции токов генератора id, iq, if и iQ.
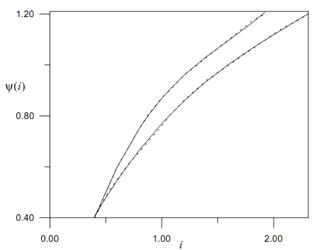
Рис. 2. Зависимости потокосцеплений ψ от токов i
Потокосцепления рассеяния осей d и q ψd и ψq могут быть определены из взаимных потокосцеплений рассеяния ψmd и ψmq следующим образом:
![]()
![]()
![]()
![]()
где Xle – реактивность утечки.
Модель энергосистемы описывается системой 16 нелинейных ОДУ первого порядка, 6 из которых относятся к электрической подсистеме, остальные 10 – к механической [1, 4, 5]. Механическая подсистема состоит из турбины со ступенями высокого (СВД) и низкого (СНД) давления, двух связей между ними (СВН и СНГ) и генератора. Одна подсистема расположена между ступенями высокого и низкого давления турбины, другая – между ступенью низкого давления турбины и генератором (рисунок 1).
В данном случае не учитывается динамика АРВ и управление турбиной [3]. Учитывается динамика демпферных обмоток оси q и насыщение генератора. В результате получим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где
![]()
![]()
здесь Xle, Xlf и XlQ - реактивности утечки;
id, iq, if, iQ, ecd, ecq, ω1, θ1, ω2, θ2, ω3, θ3, ω4, θ4, ωr и δr - переменные системы. При моделировании использовались следующие параметры генератора и линии в о.е.:
Rf=0.001252, Ra=0.0045, RQ=0.009957, Rl=0.00172,
Xl=0.08366, Xle=0.145, Xlf=0.1061, XlQ=0.3819,
d0= -0.1626, d1=1.7374, d2= -0.8939, d3=0.1876,
q0=0.0635, q1=0.9808, q2= -0.3244, q3=0.0489.
Механические коэффициенты демпфирования, инерционности и жесткости в о.е.:
D1=0.02677, D2=0, D3=0.0415, D4=0, D5=0.06832,
M1=0.4930, M2=0.03107, M3=2.8383, M4=0.1156, M5=1.6512,
K12=107.611, K23=61.705, K34=141.413, K45=175.208.
Для случая без насыщения значения d0, d2, d3, q0, q2 и q3 в уравнениях 1 и 2 были приняты равными нулю [3]. Рабочие состояния (н.у.) определены путем подстановки нулей вместо производных переменных состояния в систему уравнений.
На рисунке 3 показана зависимость действительных и мнимых частей собственных значений от µ при Pe=0.9, Qe=0.4358 и υt=1.0, где µ - относительный уровень компенсации. Было получено 14 комплексных и 2 действительных собственных значения. Поскольку матрица Якоби действительна, комплексно сопряжены каждые комплексные величины собственных значений, существует 7 колебательных режимов. Из них 2 режима – электрические и 5 – механические. Режим с наименьшей частотой – режим качания или электромеханический режим, остальные 4 механических режима – режимы вращения. Два из режимов вращения, третий и четвертый, сильно демпфируются и имеют большие частоты (1030 рад/с и 1450 рад/с). Следовательно, они не будут взаимодействовать с электрическими режимами при реальных уровнях компенсации. Два действительных собственных значения отрицательны, одно относится к обмоткам поля, второе – к демпферным обмоткам.
При небольших µ, частоты электрических режимов приблизительно 314 рад/с. С увеличением µ, подсинхронная и сверхсинхронная частоты разделяются. Сверхсинхронная частота демпфируется, тогда как подсинхронная – нет. Рассмотрим подробнее подсинхронную частоту и как связанный с ней режим взаимодействует со вторым и первым режимами вращения.
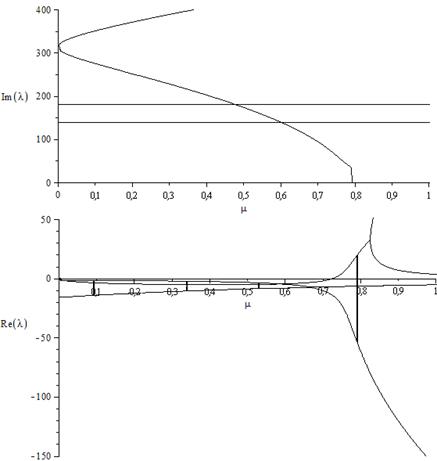
Рис.3. Зависимость действительных и мнимых частей собственных значений
от µ при Qe=0.4358, Pe=0.9 и υt=1.0 (Без насыщения)
При увеличении µ частота подсинхронного электрического режима уменьшается и достигает частоты второго режима вращения (199 рад/с) при µ=0.88103. Из этого следует, что собственные значения второго режима вращения сдвигаются вправо и, пересекая мнимую ось, попадают в правую половину комплексной плоскости при µ=Н=0.88103. Следовательно, второй режим вращения теряет устойчивость из-за бифуркации Хопфа [2]. В данном случае частота электрического режима пересекает второй режим вращения при значениях µ<1 вследствие одной области взаимодействия.
При потере устойчивости точки равновесия из-за этого взаимодействия, при увеличении µ устойчивость не восстанавливается. Из этого можно заключить, что в данном случае существует лишь одна точка бифуркации Хопфа.
Рассмотрим влияние насыщения стали. На рисунке 4 показана зависимость действительных и мнимых частей собственных значений от µ. При увеличении µ частота подсинхронного электрического режима уменьшается и достигает частоты второго режима вращения (199 рад/с) при µ=0.842003.
Из этого следует, что собственные значения второго режима вращения сдвигаются вправо и, пересекая мнимую ось, попадают в правую половину комплексной плоскости при µ=Н=0.842003. Таким образом, второй режим вращения теряет устойчивость из-за бифуркации Хопфа.
На рисунке 5 изображена зависимость угла ротора δr от уровня компенсации µ. Определили, что точка бифуркации Хопфа ‑ µ=Н=0.842003. Сравнивая рисунки 4 и 5, видим, что при учете насыщения бифуркация Хопфа происходит при меньшем значении, а именно при 0.842003, тогда как без учета насыщения 0.881003. Другими словами, точка бифуркации Хопфа сместилась влево [2].
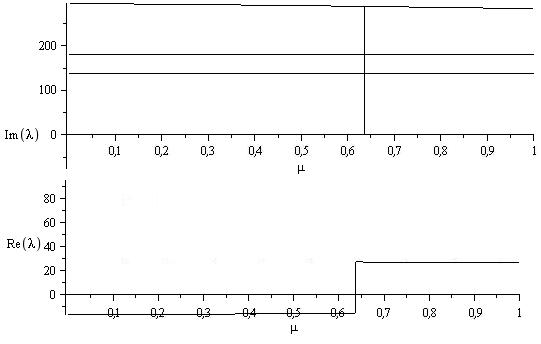
Рис.4. Зависимость действительных и мнимых частей собственных значений от µ при Qe=0.4358, Pe=0.9 и υt=1.0 (С учетом насыщения)
Насыщение стали приводит к уменьшению области демпфирования, дестабилизируя систему. Чтобы показать, что дестабилизация происходит из-за насыщения стали, на рисунке 5 изобразили зависимость участков бифуркации Хопфа на плоскости Ре‑ µ при Qe=0.4358 и υt=1.0.
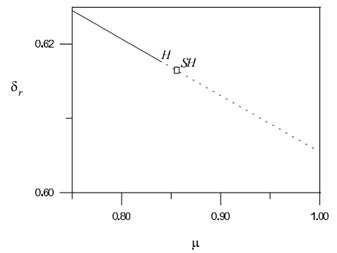
Рис. 5. Зависимость угла ротора генератора δr от уровня компенсации µ при Qe=0.4358, Pe=0.9 и υt=1.0. Непрерывная линия соответствует устойчивому равновесию, пунктирная – неустойчивому
Все режимы, расположенные левее пунктирной кривой, демпфируются, тогда как второй режим вращения, расположенный правее пунктирной кривой, не демпфируется. Из рисунка 5 следует, что насыщение стали снижает уровень компенсации для всех значений Ре, при котором происходит подсинхронный резонанс. Чем меньше значение Ре, тем больше дестабилизирует насыщение стали систему.
Вывод
В процессе исследования показано, что в энергосистемах, использующих устройства FACTS, возможно появление на подсинхронных частотах вращения турбогенераторов нежелательных резонансных режимов – электромеханического резонанса.
Переход к электромеханическому резонансу может осуществляться посредством бифуркации Хопфа.
При учете насыщения стали турбогенераторов бифуркация Хопфа возникает при меньших уровнях компенсации, следовательно, область демпфирования уменьшается, делая энергосистему менее устойчивой.
Рецензенты:
Горелов В.П., д.т.н., профессор, заместитель зав. кафедрой «Электроэнергетические системы и электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Новосибирская государственная академия водного транспорта», г. Новосибирск;
Сальников В.Г., д.т.н., профессор кафедры «Электроэнергетические системы и электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Новосибирская государственная академия водного транспорта», г. Новосибирск.
Библиографическая ссылка
Рысев П.В., Рысев Д.В., Фёдоров В.К. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ВОЗНИКНОВЕНИЯ ЭЛЕКТРОМЕХАНИЧЕСКОГО РЕЗОНАНСА ОТ НАСЫЩЕНИЯ МАГНИТОПРОВОДА СТАТОРА ГЕНЕРАТОРА // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=15473 (дата обращения: 23.02.2026).



