При определении технологических потерь электрической энергии в электрических сетях необходимо учитывать температуру провода [2, 4, 5]. На кафедре «Электроснабжение промышленных предприятий» Омского государственного технического университета создан комплекс программ Ом1, позволяющий определять температуру проводов и, с ее учетом, потери электрической энергии в воздушных линиях электропередачи по четырем методам расчета. Приведенный анализ показал целесообразность использования двух подходов, основанных на методах №1 (У) [3] и №4 [6]. Метод №1 (У) для расчета неизолированных проводов представляет усовершенствованную версию, отличающуюся от исходной (метод №1 [1]) использованием уравнений (1, 2).
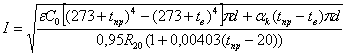, (1)
, (2)
где tпр – температура провода, °C, tв – температура воздуха, °C, d – диаметр провода, м, R20 – сопротивление провода при температуре 20°C, αк – коэффициент теплоотдачи конвекцией, ε - степень черноты поверхности провода, С0 – коэффициент излучения абсолютно черного тела, равный 5,67.10-8 Вт/(м2.К4), – мощность нагрева 1 м провода солнечным излучением, 
– коэффициенты аппроксимации.
Уравнения (1, 2) являются базовыми для разработанного алгоритма (метод №1(У), программа Ом1.1) расчета потерь, представленного на рисунке 1.
Метод №4 обладает более широкими возможностями, чем метод №1(У). Он позволяет находить потери в изолированных и неизолированных проводах. Представленный на рисунке 2 алгоритм (метод №4, программа Ом1.2) соответствует произвольному изменению условий эксплуатации проводов и варианту, когда коэффициенты теплоотдачи теплового излучения и конвекции зависят от температуры наружной поверхности провода, т.е. 
и 
. Нахождение температуры для изолированных проводов в этом случае может быть получено итерационным методом на основе уравнения:
(3)
где k – номер итерации; 
– температура окружающей среды (воздуха), °С; 
– потериактивной мощности при температуре 20 °С, Вт/м; 
– площадь поверхности проводника, 
;
– температура наружной поверхности изоляции провода, °С.
Коэффициент 
определяется выражением:
, (4)
где
– тепловое сопротивление изоляции; 
– коэффициент теплопроводности изоляции; 
– мощность притока теплоты на единицу длины и в единицу времени солнечной радиацией.
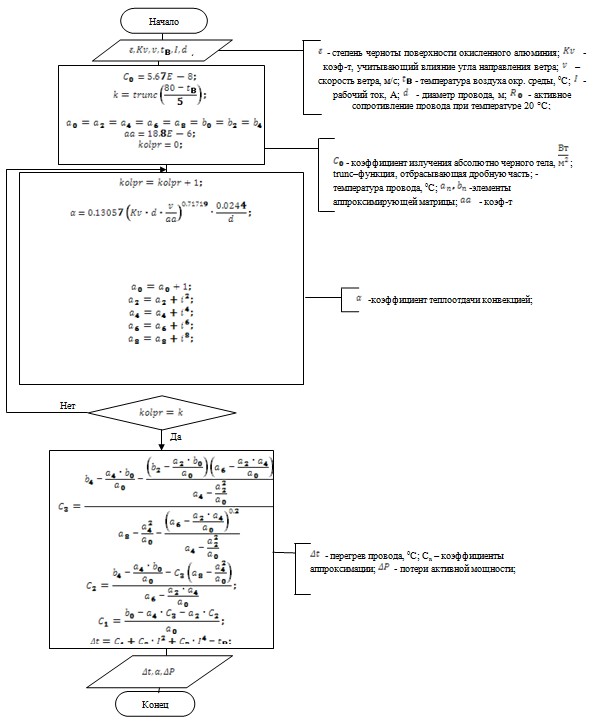
Рис. 1. Алгоритм расчета программой Ом1.1
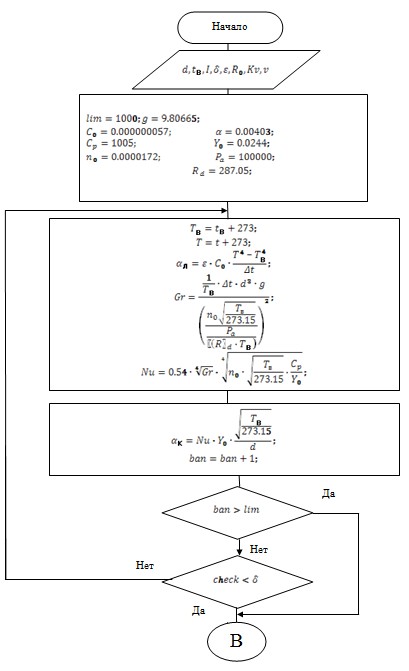
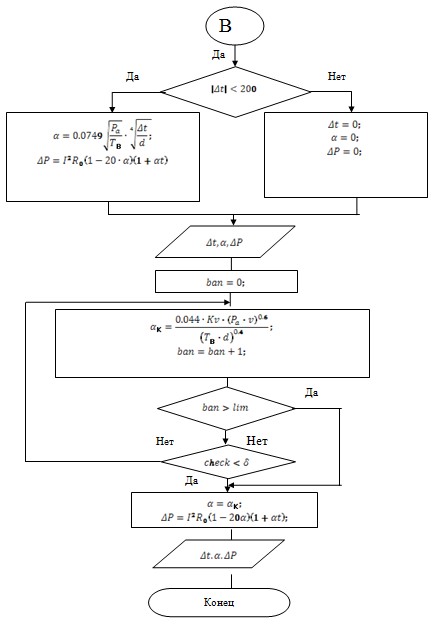
Рис. 2. Алгоритм расчета программой Ом1.2
Выражение (3) для неизолированных проводов (Sиз = 0) упрощается и, соответственно, преобразуется к уравнению:
(5)
Наиболее высокая точность определения
реализована по закону Стефана-Больцмана:
, (6)
где Tвнеш – абсолютная температура поверхности изоляции, K; Tв – абсолютная температура воздуха, K; 
, K.
Исходя из критериальных уравнений конвективного теплообмена и критериев Нуссельта и Прандтля, выведено уравнение коэффициента теплоотдачи при естественной и вынужденной конвекциях для изолированных и неизолированных проводов с учетом атмосферного давления:
, 
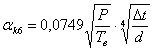(7)
где P – атмосферное давление, Па; 
– коэффициент угла атаки ветра; v – скорость ветра.
Достоверность расчетов по входящим в состав комплекса Ом1 программ Ом1.1 и Ом1.2 проведена на основании сравнения с расчетами, основанными на стандартах CIGRE, IEEE и МКЭ [7].Численное моделирование было проведено для провода марки
429-AL1/56-ST1 A/.
Условия численного эксперимента: провод 429-AL1/56-ST1 A (диаметр 
м, 
Ом/м); токовая нагрузка600А; температурный коэффициент электрического сопротивления
град-1; степень черноты поверхности провода 
;поправочный коэффициент на угол атаки ветра 
;температура воздуха
;скорость ветра 2 мс;cолнечная радиация 980 Вт/м2;высота над уровнем моря 300 м; Расчеты по методу №4 проводились с предположением наличия вынужденной конвекции.
Приведенные в таблице 1 обозначения расшифровываются следующим образом: CIGRE – метод, основанный на стандарте расчета линий электропередач, разработанный Международным Советом по большим электроэнергетическим системам; IEEE – метод, основанный на стандарте расчета линий электропередач, разработанный Институтом инженеров электротехники и электроники; МКЭ – метод расчета температуры проводника, основанный на современном численном методе – методе конечных элементов.
Результаты сравнения приведены в таблице 1.
Таблица 1
Результаты сравнения
|
Метод |
Без учета солнечной радиации |
С учетом солнечной радиации |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
CIGRE |
– |
– |
– |
– |
55,70 |
0,00 |
4,50 |
3,15 |
3,57 |
|
IEEE |
– |
– |
– |
– |
53,30 |
4,31 |
0,00 |
1,30 |
0,89 |
|
МКЭ |
– |
– |
– |
– |
54,00 |
3,05 |
1,31 |
0,00 |
0,41 |
|
№1(У) |
47,40 |
14,90 |
11,10 |
12,20 |
51,50 |
7,54 |
3,38 |
4,63 |
4,24 |
|
№4 |
49,40 |
11,30 |
7,32 |
8,52 |
54,40 |
2,33 |
2,06 |
0,74 |
1,15 |
°С
%
%
%
Наряду с величинами температуры провода, в таблицах представлены значения отклонений температур, определяемые по формулам:
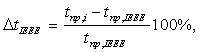(8)
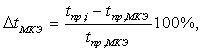
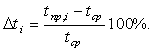(9)
где 
– значение температуры провода, найденное по методу CIGRE; 
– значение температуры провода, найденное по методу IEEE; 
– значение температуры провода, найденное по методу МКЭ; 
– значение температуры провода, определяемое соответствующим методом, 
– отклонение от среднего значения температуры для i-го метода.
Вывод: результаты расчетов по всем методам с учетом солнечной радиации близки друг к другу, что свидетельствует о возможности практического применения всех методов.
Рецензенты:
Харламов В.В., д.т.н., профессор, заведующий кафедрой «Электрические машины и общая электротехника» ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск;
Черемисин В.Т., д.т.н., профессор, директор Научно-исследовательского института энергосбережения на железнодорожном транспорте (НИИЭ ОмГУПС), заведующий кафедрой «Подвижной состав электрических железных дорог» ФГБОУ ВПО «Омский государственный университет путей сообщения», г. Омск.
Библиографическая ссылка
Петрова Е.В., Гиршин С.С., Горюнов В.Н., Бубнов А.В., Кузнецов Е.А. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ПОТЕРЬ В ПРОВОДАХ ВОЗДУШНЫХ ЛИНИЙ С УЧЕТОМ ТЕМПЕРАТУРЫ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=15251 (дата обращения: 20.04.2024).