Взаимодействие разреженных потоков твердых частиц является чрезвычайно сложным процессом, который сопровождается как столкновениями между отдельными частицами, так и взаимодействием (перекрытием) потоков в целом. Такие виды взаимодействия приводят к изменению структуры и формы потоков, а также образованию новых – отраженных [1]. Проведенный ранее анализ литературных источников по взаимодействию дисперсных потоков [2,3] показал, что большинство известных работ относятся к определению числа взаимных столкновений частиц; другие же стороны взаимодействия остаются малоизученными. Это обусловлено сложностью характера взаимодействия разреженных потоков, который сопровождается как столкновениями частиц, перераспределением объемной плотности, так и изменением формы и структуры потоков. В некоторых случаях в результате таких взаимодействий могут образоваться новые частицы (дробление в результате столкновений). Однако такой характер взаимодействия является достаточно редким для большинства твердых материалов, определяется многими факторами и наблюдается при скоростях более 20 м/с. Такие режимы практически не являются рабочими в смесительных устройствах, чаще имеют место в аппаратах, предназначенных для дробления и измельчения.
При пересечении и наложении разреженных потоков можно выделить и различить взаимодействия на макро- и микроуровнях [3,4]. К макроуровню относится взаимодействие потоков в целом, их полное или частичное наложение, пересечение и т. д. Основной целью изучения макровзаимодействия является исследование процесса наложения потоков.
Взаимодействие на микроуровне характеризуется непосредственно столкновениями частиц в пересекающихся потоках. Данный тип взаимодействия может приводить к изменению формы и структуры потоков, что очень важно. Наиболее существенное проявление взаимодействия частиц на микроуровне происходит в зонах перекрытия (пересечения) потоков с высокой концентрацией частиц [3], и, несомненно, как сказано выше, этот эффект влияет на движение потоков в целом (макроуровень).
Столкновения частиц в дисперсных потоках в зависимости от типа процесса может иметь как положительное, так и отрицательное влияние. На принципе контакта частиц в разреженных потоках выполнены устройства для проведения химических реакций, гранулирования и другие. Здесь количество межчастичных столкновений приводит к увеличению времени взаимодействия и повышению эффективности процесса [1–3]. При расчете и проектировании таких устройств подбирают такие режимы движения частиц, при которых число столкновений максимально. Однако столкновения частиц внутри потоков при смешении и измельчении сыпучих сред могут также оказывать негативное влияние на конечный продукт [2].
При проведении процессов смешения непредсказуемое хаотическое поведение взаимодействующих (сталкивающихся частиц) приводит к нарушению упорядоченной (требуемой) структуры потока, приводит к образованию локальных зон со скоплением частиц одного из компонентов, что повышает степень неоднородности [2].
В процессе измельчения материалов ударом столкновения между частицами внутри потока или с отраженными приводят с уменьшению скоростей движения, а, следовательно, к понижению степени измельчения [3]. Столкновения частиц в смесителях сыпучих материалов неоднозначно влияют на однородность смеси. В некоторых случаях взаимодействия частиц могут способствовать взаимному проникновению компонентов и приводить к улучшению качества смеси [2]. Однако непредсказуемый характер отражений делает процесс смешения неуправляемым и хаотичным. При этом также возникают трудности по смене режимов работы смесителя в случае перехода на другие материалы.
Для определения присутствия столкновений между частицами взаимодействующих дисперсных потоков принято использовать понятие длины свободного пробега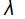 
[1].
Вследствие того, что количество соударений частиц, зависит главным образом от их концентрации в зоне взаимодействия [3], необходимо знать характер его изменения в потоке по длине и удалению от центра – начала формирования.
Расчетная схема для вычисления концентрации частиц приведена на рисунке 1.
Выделим в потоке элемент, находящийся на расстоянии sL1 от вершины потока, определяемый углом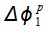 
и шириной 
.
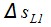Размеры величин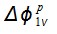 
и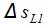 
, соответствующие 
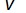-му угловому диапазону, определяются геометрическими параметрами потока и размерами частиц.
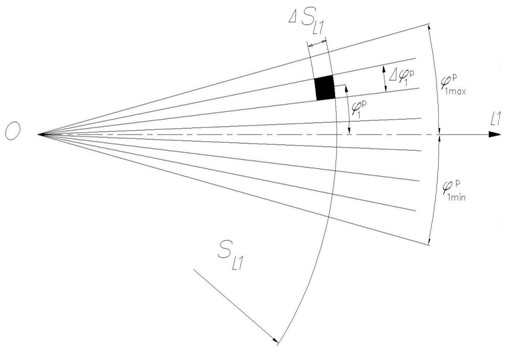
Рис. 1. Схема для определения концентрации частиц в расширяющемся дисперсном потоке
Площадь указанного элемента может быть определена выражением:
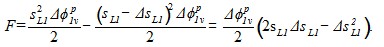. (1)
Для определения числа частиц в элементе потока воспользуемся выражениями дифференциальной функции распределения по углам рассеивания [3]. Число частиц в выделенном элементе:
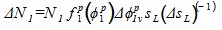. (2)
Тогда концентрация частиц в выделенной области потока вычисляется по формуле:
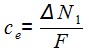, (3)
с учетом (2):
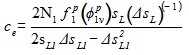. (4)
По формуле (4) можно определить концентрацию частиц в дисперсном расширяющемся потоке в зависимости от угла рассеивания и расстояния от места вылета частиц из распылителя.
Концентрацию частиц обоих потоков сs в зоне перекрытия определим как сумму концентраций частиц каждого из материалов:
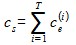. (5)
При расчете суммарной концентрации в зоне взаимодействия необходимо учитывать как форму и структуру потоков, так и взаимное расположение.
Столкновения между частицами взаимодействующих потоков имеют место при выполнении условия:
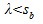. (6)
Здесь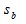 
– ширина зоны взаимодействия.
На рисунке 2 приведена расчетная схема для определения ширины зоны перекрытия потоков.
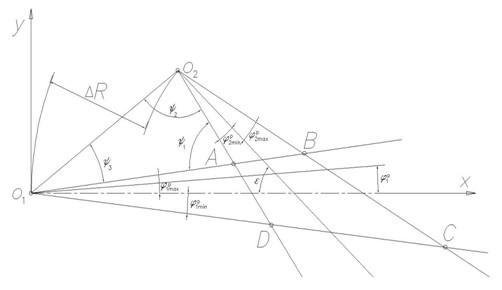
Рис. 2. Расчетная схема для определения ширины зоны перекрытия взаимодействующих потоков
При расчете в качестве исходных геометрических характеристик зоны перекрытия считаем заданными значения расстояни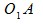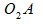й 
, 
и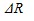 
. Определим значения углов 
:
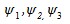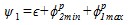. (7)
Соотношение значений углов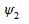 
и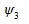 
найдем из выражения:
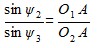. (8)
Следующим этапом является определение минимального значения ширины зоны перекрытия (расстояние АВ на расчетной схеме).
Находим расстояние от начала потока одного из компонентов (например с индексом 1) до точки В :
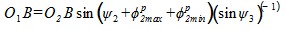. (9)
Здесь
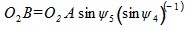. (10)
Значения углов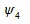 
и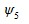 
вычисляются из выражений:
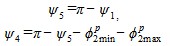. (11)
Тогда наименьшая ширина зоны перекрытия потоков определяется как разность:
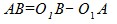. (12)
Аналогично рассчитывается максимальная ширина области взаимодействия потоков (Д С).
Макроуровень, в отличие от микроуровня, относящегося к столкновениям отдельных частиц, имеющим локальный характер, описывает взаимодействие струйных течений в целом. В случае проведения процессов смешения макровзаимодействие проявляется наложением (перекрытием) потоков и влияет на образование смеси [3]. В других процессах (ударном измельчении, разделении суспензий) макровзаимодействие наблюдается при наложении потоков, образованных при ударе. В этом случае влияние макровзаимодействия на конечный результат практически отсутствует.
Таким образом, исследование макроуровневого взаимодействия наиболее целесообразно проводить при исследовании смешения сыпучих сред.
В зависимости от расположения распылителей и формы разреженных факелов их перекрытие может быть как полным, так и частичным [4].
От степени перекрытия, взаимного расположения потоков и параметров распределения частиц в них зависит однородность получаемой смеси [4], качественным показателем которой является коэффициент неоднородности смеси. С точки зрения минимизации данного показателя наиболее предпочтительным является организация зоны перемешивания в местах полного перекрытия.
Рецензенты:
Мурашов А.А., д.т.н., заведующий кафедрой математических и естественнонаучных дисциплин Московского финансово-юридического университета, г. Ярославль;
Епархин О.М., д.т.н., профессор, директор Ярославского филиала ФГБОУ ВПО «Московский государственный университет путей сообщения», г. Ярославль.
Библиографическая ссылка
Лебедев А.Е., Зайцев А.И., Шеронина И.С. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССОВ ВЗАИМОДЕЙСТВИЯ ПЕРЕСЕКАЮЩИХСЯ РАЗРЕЖЕННЫХ ПОТОКОВ // Современные проблемы науки и образования. – 2014. – № 5. ;URL: https://science-education.ru/ru/article/view?id=14975 (дата обращения: 11.10.2024).