Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Власова К.В. 1 Волхонская Е.В. 1 Коротей Е.В. 1 Пахотин В.А. 2

---

1 ФГБОУ ВПО «Калининградский государственный технический университет», Балтийская государственная академия рыбопромыслового флота

2 ФГОУ ВПО «Балтийский Федеральный Университет имени И. Канта»

В настоящей работе рассматривается возможность повышения разрешающей способности при обработке сигналов с линейной частотной модуляцией. Исследуются два сигнала, временной сдвиг между которыми настолько мал, что их корреляционные функции получены с наложением. В этом случае для решения задачи обнаружения и оценки параметров двух сигналов по отдельности нельзя применять корреляционный анализ. Однако метод, основанный на анализе функционала правдоподобия, позволяет получать достоверные оценки параметров сигналов даже в условиях их наложения. Коэффициент корреляции при этом может достигать значения 0,9. Динамический диапазон решения ограничен только соотношением сигнал/шум. При использовании предложенного метода возможно повышение разрешающей способности в 5 раз по сравнению с корреляционным анализом. В работе представлены аналитические выражения, а также полученные на их основе результаты модельных исследований. Результаты моделирования подтверждают основные положения теории.

Статья в формате PDF

475 KB

функционал правдоподобия

корреляционная функция

статистическая теория радиотехнических систем

разрешающая способность

Сигналы с линейной частотной модуляцией

1. Власова К.В., Никитин М.А., Чугайнов А.С., Кочмарский А.В. Оценка параметров ионосферного сигнала // Вестник БФУ им. И.Канта: 2012, Вып. 4. – С. 78-84.

2. Пахотин В.А., Бессонов В.А., Молостова С.В., Власова К.В. Теоретические основы оптимальной обработки сигналов. – Калининград: Изд-во РГУ им. И. Канта, 2008. – 189 с.

3. Пахотин В.А., Бессонов В.А., Власова К.В. Разрешающая способность в радиолокации. – LAPLAMBERT Academic Pablishing, 2011. – 157 с.

4. Перов А.И. Статистическая теория радиотехнических систем. – М.: Радиотехника, 2003.

5. Перов А.И. Статистическая теория радиотехнических систем : учеб. пособ. для вузов. – М.: Радиотехника, 2003. – 400 с.

6. Тихонов В.И. Оптимальный прием сигналов. – М.: Радио и связь, 1983. – 320 с.

Сигналы с линейной частотной модуляцией (ЛЧМ-сигналы) относятся к сигналам с большой базой. Они имеют узкую корреляционную функцию и малую мощность при значительной энергии. Эти положительные качества ЛЧМ-сигналов определяют их широкое использование в различных комплексах аппаратуры.

Теоретической основой при обработке ЛЧМ-сигналов является корреляционный анализ. Максимум корреляционной функции дает возможность оценить время приема ЛЧМ-сигнала и его амплитуду. Ширина корреляционной функции зависит от девиации частоты и обеспечивает высокое разрешение ЛЧМ-сигналов по времени приема.

Корреляционный анализ, используемый для обработки ЛЧМ-сигналов, имеет ограничение по разрешающей способности, связанное с критерием Релея. Критерий Релея разделяет совокупность ЛЧМ-сигналов на ортогональные, когда коэффициент корреляции между ними равен нулю, и неортогональные, когда коэффициент корреляции отличен от нуля. В настоящей работе представлен метод, позволяющий снять ограничение Релея по разрешающей способности. Он дает возможность обрабатывать ЛЧМ-сигналы как в области их ортогональности, так и в области их неортогональности. При этом разрешающая способность при обработке ЛЧМ-сигналов увеличивается и, в принципе, оказывается зависящей от отношения сигнал/шум.

Основой метода обработки ЛЧМ-сигналов является использование при обработке дополнительного вектора – вектора разности между вектором принятого сообщения и вектором копии сигнала с оцениваемыми параметрами (вектором ). При этом появляются новые возможности при обработке ЛЧМ-сигналов. Они связаны с оценкой дисперсии шума в принятой реализации, с повышением разрешающей способности при обработке ЛЧМ-сигналов, с увеличением точности оценки параметров, с возможностью нового решения задачи обнаружения сигнала. Использование вектора разности  для обработки сигналов приводит к новой технологии, возможности которой находятся лишь в начале изучения.

В настоящей работе новая технология обработки сигналов применена для решения задачи разрешения ЛЧМ-сигналов.

Основы теории

Рассмотрим основы теории обработки ЛЧМ-сигналов, используя для простоты совокупность двух ЛЧМ-сигналов. Запишем принятое сообщение  в комплексном виде

, (1)

где , – комплексные амплитуды ЛЧМ-сигналов;

– круговая частота;

, – времена приема ЛЧМ-сигналов;

;

– конечная круговая частота;

– длительность ЛЧМ-сигнала;

– аддитивный нормальный шум со средним значением, равным нулю, дисперсией и интервалом корреляции .

Запишем на основании (1) логарифм функции правдоподобия

, (2)

где – вектор оценочных параметров сигнала, отмеченных штрихами.

Частоту  и параметр будем считать известными.

Вместе с выражением для логарифма функции правдоподобия запишем функционал правдоподобия. Он более удобен для дальнейшего анализа

. (3)

Функционал правдоподобия представляет собой квадрат модуля вектора разности между вектором принятого сообщения и вектором – копией сигнала с оценочными параметрами (вектора ).

Функция правдоподобия представляет собой условную плотность распределения параметров сигнала. Максимум функции правдоподобия определяет наиболее вероятные оценочные параметры сигнала. В связи с этим, дифференцируя (3) по амплитудам и и приравнивая дифференциалы к нулю, получим систему уравнений правдоподобия

,

, (4)

где черта сверху означает интегрирование;

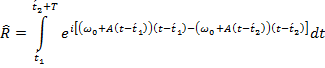
- нормированный коэффициент корреляции между двумя ЛЧМ-сигналами;

*- комплексное сопряжение.

Система уравнений (4) решается относительно и при произвольных значениях и

,

. (5)

При выражения (5) определяют классический корреляционный анализ ЛЧМ-сигналов с максимумами в точках и. Если , то выражения (5) не имеют четко выраженных максимумов, а, следовательно, не могут быть использованы для обработки ЛЧМ-сигналов в области их неортогональности. Для решения задачи разрешения ЛЧМ-сигналов, выражения (5) необходимо подставить в функционал правдоподобия (3). В этом случае используются возможности вектора, и при этом уменьшается количество неизвестных в (3). Подставим (5) в (3) и проведем алгебраические преобразования с учетом (4). В результате получим функционал правдоподобия в виде

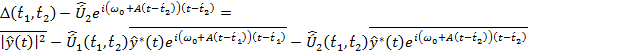. (6)

Данный функционал является поверхностью в двухмерном пространстве,. Перебирая все значения и в области их определения, можно получить полную поверхность функционала правдоподобия. Максимум поверхности функционала реализуется в точке и при и . По своему смыслу минимум значения функционала (3) определяет дисперсию шума.

Таким образом, используя минимум функционала правдоподобия, как критерий, можно полностью решить задачу разрешения двух ЛЧМ-сигналов при значениях , отличающихся от нуля.

Рассмотрим вопрос о рабочей области данного метода решения задачи разрешения двух ЛЧМ-сигналов. Для этого воспользуемся выражением для дисперсии амплитуд ЛЧМ-сигналов (дисперсии Рао – Крамера). Вывод этого выражения основан на использовании информационной матрицы Фишера, элементы которой определяются выражением

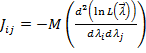, (7)

где – оператор математического ожидания.

Элементы матрицы Фишера находятся в точке минимума функционала правдоподобия при и , когда и . Выполняя дифференцирование (2) согласно (7), получим информационную матрицу Фишера

. (8)

Диагональные элементы матрицы, обратной матрице Фишера, определяют дисперсии амплитуд ЛЧМ-сигналов

, (9)

где – количество некоррелированных отсчетов шума на интервале .

Из выражения (9) следует, что в результате обработки дисперсия уменьшилась в раз. Если ввести значение дисперсии, при , то относительная дисперсия имеет простую зависимость от

. (10)

При изменении от 0 до 0,9, относительная дисперсия увеличивается на 7 дБ. Эта область изменений может быть принята за рабочую область представляемого метода решения задачи разрешения двух ЛЧМ-сигналов.

Увеличение дисперсии на 7 дБ в точке это плата за высокое разрешение сигнала. Задача разрешения двух ЛЧМ-сигналов может быть решена и при , но при этом необходимо иметь высокое (более 7 дБ) отношение сигнал/шум в принятой реализации.

Результаты модельных расчетов

Представим результаты модельных расчетов, отображающие возможность обработки принятого сообщения, содержащего два ЛЧМ-сигнала. При модельных расчетах приняты следующие параметры ЛЧМ-сигналов: амплитуды, ; начальные фазы, ; конечная частота кГц; длительность сигнала мс; время приема первого ЛЧМ-сигнала мс; время приема второго ЛЧМ-сигнала может быть различным. Отношение сигнал/шум равно 0 дБ.

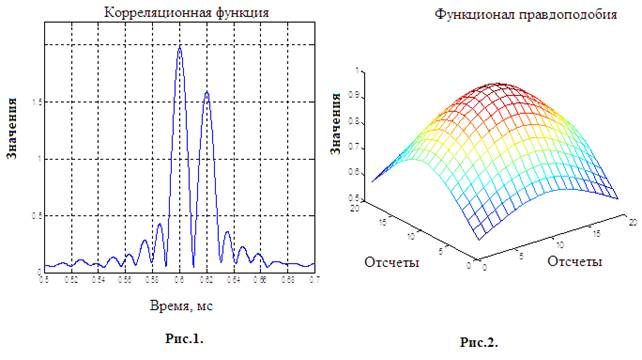
Пусть принята реализация, содержащая два ЛЧМ-сигнала. Различие времени приема мс. В этом случае коэффициент корреляции близок к нулю и корреляционный анализ дает возможность оценить по наблюдаемым максимумам на рис.1 время приема и амплитуды сигналов ЛЧМ. Поверхность обратного функционала правдоподобия показана на рис.2. Единственный максимум этой поверхности определяет оценочные параметры двух ЛЧМ-сигналов: , , , . Значение максимума поверхности оценивает дисперсию шума.

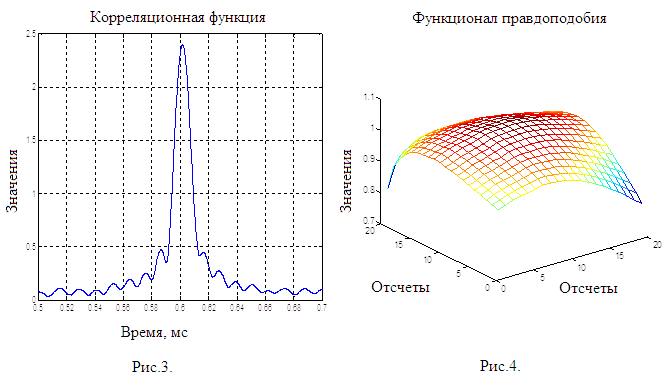
При уменьшении различия во времени приема до значения мкс, коэффициент корреляции между ЛЧМ-сигналами возрастает до значения . Корреляционная функция имеет вид одного максимума, значение которого меняется в зависимости от разности фаз двух ЛЧМ-сигналов (рис.3). Поверхность обратного функционала правдоподобия (рис.4) имеет единственный максимум, определяющий совокупность параметров: , , , .

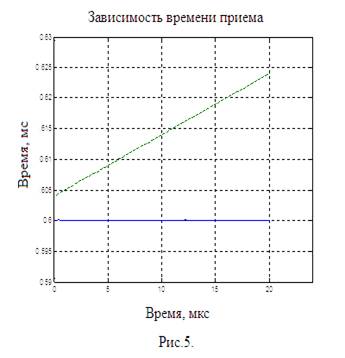
На рис.5 показаны изменения оценочных времен приема двух ЛЧМ-сигналов при следующих условиях. Значение постоянно и равно мс, значение меняется в пределах от мс до мс. Этим обеспечивается изменение коэффициента корреляции между ЛЧМ-сигналами от и ниже.

Классическое разрешение ЛЧМ-сигналов при девиации частоты кГц определено значением мкс. В результате модельных расчетов в соответствии с новым методом решения разрешение ЛЧМ-сигналов возможно при мкс. Следовательно, разрешение двух ЛЧМ-сигналов может быть увеличено по сравнению с классикой в 5 раз. Это подтверждает основные теоретические положения представляемого метода Отношение сигнал/шум, в котором возможно увеличение разрешения двух ЛЧМ-сигналов, согласно модельным расчетам, может достигать -20 дБ. Динамический диапазон представляемого метода ограничен уровнем шума в принятой реализации. Даже пятикратное уменьшение амплитуды второго ЛЧМ-сигнала позволяет с удовлетворительной точностью оценить время приема слабого сигнала и его амплитуду. Влияние боковых лепестков корреляционной функции ЛЧМ-сигналов, ограничивающий динамический диапазон корреляционного анализа, не отмечается.

Заключение

В настоящей работе представлена новая методика решения задачи разрешения двух ЛЧМ-сигналов. Она основана на использовании дополнительной информации, которую позволяет получить вектор разности между вектором принятого сообщения и вектором копии сигнала с оценочными параметрами. Новая методика снимает Релеевское ограничение на разрешающую способность и дает возможность увеличить практически разрешение двух ЛЧМ-сигналов по крайней мере в 5 раз по сравнению с методом корреляционного анализа. Динамический диапазон обработки ЛЧМ-сигналов по новой методике ограничен лишь уровнем шума. Он значительно превышает динамический диапазон обработки методом корреляционного анализа.

Исследование выполнено в рамках государственного задания на проведение научно-технических работ, договор №2013-4 ГЗ от 01 января 2013 года.

Рецензенты:

Захаров В.Е., д.ф.-м.н., профессор, заведующий кафедрой радиофизики и информационной безопасности Балтийского федерального университета им. И. Канта, г. Калининград;

Никитин М.А., д.ф.-м.н., профессор кафедры телекоммуникаций Балтийского федерального университета им. И. Канта, г. Калининград.

Библиографическая ссылка