Решение уравнения Фоккера – Планка
В работе [3] мы предложили модель финансового инструмента, которая описывается следующей системой стохастических дифференциальных уравнений (СДУ):
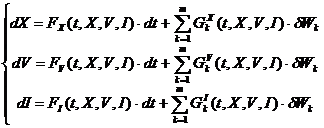, (1)
где δW – это бесконечно малый
винеровский «шум», определяемый выражением 
, 
– это случайная величина, распределенная
по нормальному закону распределения с нулевым математических ожиданием и
единичной дисперсией (
), X – цена, V –объем и I –
открытый интерес некоторого финансового инструмента.
При этом условную плотность
распределения вероятностей 
состояния системы (1)
можно найти из уравнения Фоккера – Планка (УФП) [1, 2, 5].
Далее, в работе [4]была построена модель краткосрочной торговли, которуюможно представить следующей системой СДУ:
(2)
Системе (2) соответствует следующее УФП:
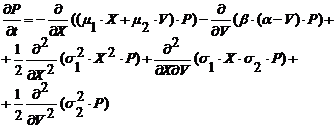, (3)
где 
.
Для решения данного уравнения воспользуемся принципом детального баланса [2].
УФП (3) можно записать в следующем виде:
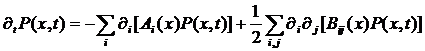(4)
Цена X и объем V являются четными переменными, то есть выполняется равенство:
,
где 
.
С учетом вышеуказанной четности, необходимые и достаточные условия детального баланса для уравнения Фоккера – Планка следующие:
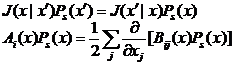, (5)
где Ps(x) – стационарная плотность распределения вероятностей, J(x|x´) – вероятность скачка.
В нашем случае x– это вектор, состоящий из цены и
объема, то есть 
, а коэффициенты сноса и
диффузии уравнения (4) могут быть записаны в следующей матричной форме:
, 
Потребуем выполнение условий детального баланса. Второе уравнение (5) приводит к следующей системе:
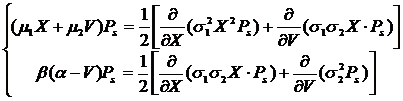(6)
Систему (6) можно переписать в следующем виде:
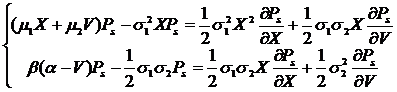
Умножим первое уравнение на σ2/(σ1X) и вычтем из него второе, получим следующее выражение:
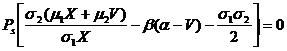(7)
При этом в качестве второго уравнения системы можно выбрать любое уравнение из (6). Тривиальное решение уравнения (7) Ps=0 нам не подходит, поэтому уравнение (7) даст следующее ограничение на решение:
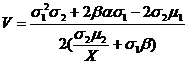(8)
Ps найдем из второго уравнения (6).
Общее решение выражается через произвольную функцию сложного аргумента:
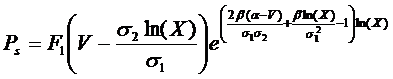(9)
В случае если объем торгов равен нулю V=0, то в модели краткосрочной торговли остается только цена X, распределения вероятностей которой будет иметь логнормальный вид:
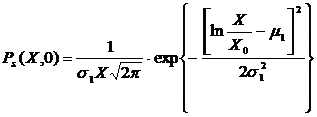(10)
Найдем решение задачи Коши для уравнения (9) с начальным условием (10).
Подставляя в общее решение (9) начальные данные (10), получим:
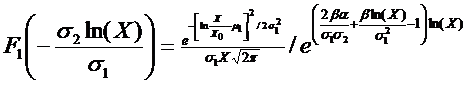(11)
Введем следующее обозначение:
,
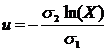откуда определяем X:
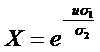
Отсюда находим функцию F1:
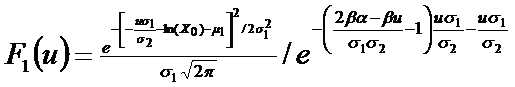(12)
Итоговое решение получается путем подстановки F1(u) в (9), где u определяется выражением:
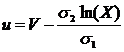
Таким образом, с помощью метода детального баланса получили стационарную плотность распределения вероятностей Ps при ограничении (8).
Численные эксперименты
В качестве примера были выбраны акции ММВБ Роснефть (ROSN). Данные были взяты за период с 11.01.2009 по 03.06.2009 с интервалом 1 день. Для процессов, которые определяются первым и вторым уравнением системы (2), были подобранны параметры (µ1=0.00005,µ2=10-8, σ1=0.02,α=1.413·107, β=0.05, σ2=4·106) и с помощью схемы Эйлера получено решение. На рисунке 1 показаны четыре версии процесса, моделирующего цены ROSNв сочетании с исходными данными:
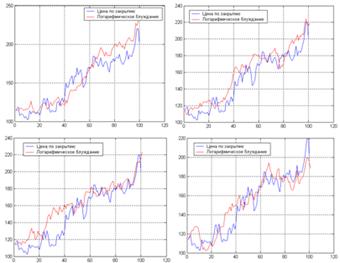
Рис. 1. Моделирование цены
В качестве меры уровня притяжения 
для процесса, моделирующего объем, было
выбрано среднее выборочное ряда V.На рисунке 2 продемонстрировано
несколько версий данного процесса, с вышеуказанными параметрами, в сочетании с
исходными данными по объему:
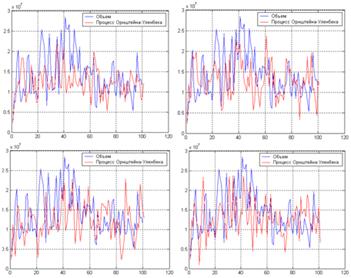
Рис. 2. Моделирование объема
Заключение
В данной работе была получена стационарная плотность распределения вероятностей для предложенной в работе [4] модели краткосрочной торговли путем решения УФП с помощью принципа детального баланса.
Для акций ММВБ Роснефть были подобраны параметры краткосрочной модели и осуществлено численное моделирование цены, объема и плотности распределения вероятностей.
При численной реализации в качестве меры уровня притяженияαдля процесса, задаваемого вторым уравнением системы (2), было предложено использовать среднее выборочное ряда V.
Дальнейшие работы могут быть связаны с идентификацией параметров предложенных моделей, вычислением ряда характеристик (среднее, дисперсия и т.д.), построением и решением модели долгосрочной торговли, учитывающей открытый интерес, выводом формул для тестирования переменной структуры параметров моделей. Также перспективным направлением является разработка краткосрочной модели, которая учитывает открытый интерес с использованием лаговых переменных.
Следует отметить, что рассмотренную в работе модель (2) можно улучшить, если в качестве второго уравнения этой системы выбрать логарифмический процесс Орнштейна –Уленбека. Выбор этой модификации будет целесообразен ввиду положительности величины объема.
Рецензенты:Семенчин Е.А., д.ф.-м.н., профессор, зав. кафедрой высшей алгебры и геометрии Кубанского государственного университета, г.Краснодар.
ЛебедевК.А., д.ф.-м.н., профессор кафедры прикладной математики Кубанского государственного университета, г. Краснодар.
Библиографическая ссылка
Кесиян Г.А. РЕШЕНИЕ УРАВНЕНИЯ ФОККЕРА – ПЛАНКА ДЛЯ СТОХАСТИЧЕСКОЙ МОДЕЛИ КРАТКОСРОЧНОЙ ТОРГОВЛИ МЕТОДОМ ДЕТАЛЬНОГО БАЛАНСА // Современные проблемы науки и образования. – 2014. – № 2. ;URL: https://science-education.ru/ru/article/view?id=12385 (дата обращения: 10.09.2024).