Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Носов Г.В. 1 Трофимович К.А. 1

---

1 ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет»

Предложена методика определения параметров экранированного однофазного шинопровода в установившемся режиме при синусоидальном токе. При этом рассчитываются сопротивление и индуктивность, сила, действующая на шины, и коэффициент теплообмена, которые находятся с учетом влияния экрана, поверхностного эффекта и эффекта близости, частоты синусоидального тока, материала шин, их температуры и температуры изоляции. Разработанная методика получена на основе уравнений электромагнитного поля, которые могут быть запрограммированы, например, в среде Mathcad для инженерного расчета параметров однофазных шинопроводов при их автоматизированном проектировании. При определенных размерах шинопровода сила, действующая на шину, равна нулю, причем с увеличением частоты тока сопротивление шинопровода возрастает, а индуктивность уменьшается. Достоверность методики подтверждается удовлетворительным совпадением результатов расчета сопротивления и индуктивности с результатами, полученными при помощи программы компьютерного моделирования Elcut.

Статья в формате PDF

166 KB

сила

индуктивность

сопротивление

шинопровод

однофазный

экран

параметры

1. Дьяконов В.П. Mathcad 8/2000: специальный справочник. – СПб.: Издательство Питер, 2000. – 592 с.

2. Методы и средства автоматизации профессиональной деятельности: учебн. пособие / А.С. Глазырин, Д.Ю. Ляпунов, И.В. Слащев, С.В. Ляпушкин. – Томск: Изд-во Томского политехнического университета, 2007. – Ч. 1. – 199 с.

3. Татур Т.А. Основы теории электромагнитного поля: справочное пособие. – М.: Высшая школа, 1989. – 271 с.

4. Теоретические основы электротехники: учебник для вузов / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПб.: Питер, 2003. – Т. 3. – 377 с.

5. Теория электрических аппаратов / под ред. Г.Н. Александрова. – М.: Высшая школа, 1985. – 312 с.

Введение

Для электропитания электрофизических установок в ряде случаев применяются однополосные экранированные однофазные шинопроводы со сплошными параллельными шинами прямоугольного сечения, расположенными согласно рисунку.

При проектировании таких шинопроводов и подключенного к ним электрооборудования необходимо знать в установившемся режиме при синусоидальном токе такие параметры, как сопротивление и индуктивность, коэффициент теплообмена поверхности шин при их заданной температуре, максимальную силу, действующую на шины, причем эти параметры должны определяться с учетом влияния экрана, поверхностного эффекта и эффекта близости [3-5]. Поэтому разработка методики расчета параметров этих шинопроводов представляется актуальной задачей. В данной статье предложена методика, полученная на основе уравнений электромагнитного поля, которые программируются в среде Mathcad [1] для автоматизированного инженерного расчета параметров рассматриваемого однофазного шинопровода.

Сопротивления и индуктивности шин при постоянном и синусоидальном токе с учетом частоты, удельной проводимости материала шин, влияния экрана, поверхностного эффекта и эффекта близости могут быть найдены при помощи программы компьютерного моделирования Elcut [2]. Однако отсутствие расчетных формул и необходимость моделирования для каждого конкретного шинопровода затрудняет анализ большого числа вариантов и ограничивает применение этой программы при инженерных расчетах. Поэтому разработка методики расчета параметров экранированного однофазного шинопровода на основе уравнений и законов электромагнитного поля актуальна и является предметом рассмотрения в настоящей работе.

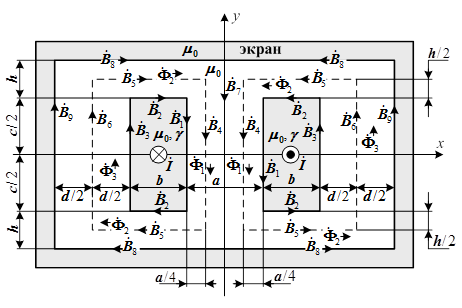
Рисунок. Однофазный шинопровод с металлическим экраном и комплексом действующего значения тока в шинах: (Гн/м) – магнитная проницаемость шин, экрана и изоляции; – удельная проводимость материала шин (1/Ом·м); «» – направление тока «к нам» по оси z; «» – направление тока «от нас»; – комплексы действующих значений индукций; – комплексы действующих значений магнитных потоков; – размеры шинопровода

Допущения

Для получения расчетных формул сделаем следующие допущения.

1. Изоляцией шин служит воздух, другой газ или жидкость, например, трансформаторное масло. Изоляция заполняет пространство между шинами и экраном, причем рассчитываемый коэффициент теплообмена поверхности шин с изоляцией [Вт/(м2·°С)] определяется условиями теплоотвода благодаря естественной или вынужденной конвекции, а также теплоизлучению [5].

2. Вся толща шин характеризуется постоянными значениями температуры (°С) и удельной проводимости (1/Ом·м), причем [5]

, (1)

где – удельная проводимость шин при температуре изоляции (°С);

– постоянный температурный коэффициент (1/°С).

3. Растекание тока вдоль шин (краевой эффект) учитывать не будем, считая при этом, что площадь поперечного сечения шин (м2) и их внешний периметр (м) постоянны.

4. Электромагнитное поле внутри металлического неферромагнитного экрана отсутствует, т.е. экран полностью непроницаем для синусоидального электромагнитного поля, изменяющегося с частотой тока f.

5. Будем исходить из представления о двух одномерных электромагнитных волнах [3, 4], проникающих в шины перпендикулярно их поверхностям вдоль осей x и y согласно рисунку.

Методика расчета

Для внешнего магнитного поля в пространстве между шинами и экраном на основании закона полного тока в интегральной форме [3] запишем уравнения:

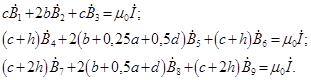(2)

Комплексы действующих значений магнитных потоков (Вб/м), обозначенных на рисунке, определим, используя аппроксимацию магнитных потоков квадратным уравнением:

; ; , (3)

причем из равенств имеем

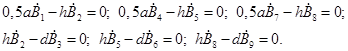(4)

Из решения уравнений (2, 4) находим индукции , а затем, согласно (3), рассчитываем магнитный поток и индуктивность внешнего магнитного поля шинопровода (Гн/м):

. (5)

Составляющие магнитной индукции внутреннего переменного электромагнитного поля и плотность тока в шине () будем рассчитывать в функциях координат x и y согласно рисунку по следующим уравнениям в комплексной форме [3, 4]:

; (6)

; (7)

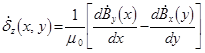, (8)

где – комплексы действующих значений проекций вектора магнитной индукции на оси x и y соответственно; – комплекс действующего значения плотности тока в шине, совпадающий по направлению с осью z и направлен «к нам»; – угловая частота тока и электромагнитного поля; – мнимая единица.

С учетом граничных условий на поверхности шины (), приведенных на рисунке, решением уравнений (6-8) будут следующие функции и константы внутреннего электромагнитного поля:

; (9)

; (10)

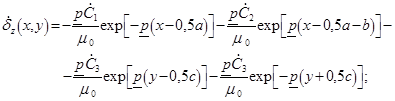(11)

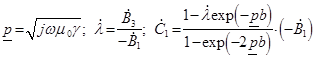; (12)

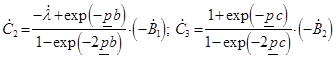; (13)

, (14)

где – модуль действующего значения вектора магнитной индукции внутреннего электромагнитного поля.

Сопротивление шинопровода (Ом/м) найдем на основе закона Джоуля-Ленца в дифференциальной форме [3, 4] и плотности тока (11):

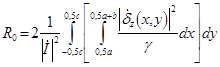, (15)

а индуктивность шин (Гн/м) внутреннего магнитного поля определим, исходя из запасенной энергии в шинах [3, 4] и индукции (14):

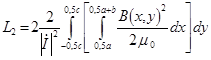, (16)

тогда с учетом (5, 16) запишем индуктивность шинопровода (Гн/м):

. (17)

Для расчета силы воздействия электромагнитного поля на шины представим комплексы действующих значений составляющей магнитной индукции (9) и плотности тока (11) в виде функций времени t и координат x, y [4]:

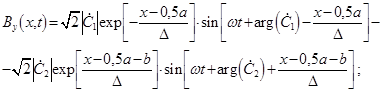(18)

(19)

где

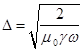(20)

– эквивалентная глубина проникновения синусоидального электромагнитного поля в проводящее полупространство.

В результате сила при максимуме (Н/м), действующая на шину, составит [3]:

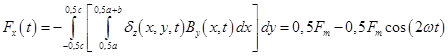. (21)

Для определения необходимого коэффициента теплообмена при заданных температурах шин и изоляции воспользуемся уравнением теплового баланса для шины [5]:

,

тогда

. (22)

Результаты расчета

По запрограммированным в среде Mathcad [1] формулам (1-22) и по программе Elcut [2] были проведены расчеты шинопроводов. В табл. 1-3 приведены результаты этих расчетов

при частотах f=50; 100; 200 (Гц) и токе (кА) для медных шин [5]: (°С); (См/м); (1/°С); (°С); (См/м); b=50 (мм); c=100 (мм).

Таблица 1

Параметры шинопровода с медными шинами при частоте тока f=50 (Гц)

Таблица 2

Параметры шинопровода с медными шинами при частоте тока f=100 (Гц)

Таблица 3

Параметры шинопровода с медными шинами при частоте тока f=200 (Гц)

Заключение

1. Предложенная методика расчета позволяет определять для экранированного однофазного шинопровода в установившемся режиме при синусоидальном токе сопротивление и индуктивность, силу, действующую на шины, коэффициент теплообмена, которые находятся с учетом влияния экрана, поверхностного эффекта и эффекта близости, частоты синусоидального тока, материала шин, их температуры и температуры изоляции.

2. Разработанная методика получена на основе уравнений электромагнитного поля, которые могут быть запрограммированы, например, в среде Mathcad для инженерного расчета параметров однофазных шинопроводов при их автоматизированном проектировании.

3. При определенных размерах шинопровода сила, действующая на шину, равна нулю, причем с увеличение частоты тока сопротивление шинопровода возрастает, а индуктивность уменьшается.

4. При увеличении расстояния между шинами и расстояний между шиной и экраном сопротивление и индуктивность шинопровода возрастают.

5. Достоверность методики подтверждается удовлетворительным совпадением результатов расчета сопротивления и индуктивности с результатами, полученными при помощи программы компьютерного моделирования Elcut.

Работа выполнена в рамках государственного задания «Наука» 7.2826.2011 «Разработка и создание гибридной модели энергоблоков электростанций».

Рецензенты:

Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск.

Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В.Е. Зуева СО РАН, г. Томск.

Библиографическая ссылка