При производстве этаноламинов важной является стадия, в процессе которой осуществляется получение фракций этаноламинов в виде моноэтаноламинов, диэтаноламинов и триэтаноламинов.
Все процессы производства автоматизированы с помощью современных систем управления.
В настоящей работе ставится цель математического исследования управляемости системы автоматизации.
Для анализа свойств системы, а именно управляемости и устойчивости, предпочтительно использовать линейные или линеаризованные модели объектов управления. Математическая модель реактора-смесителя существенно не линейная. При этом линеаризацию модели целесообразно провести в окрестности стационарного состояния объекта: [ОЭ]ст, [МЭА]ст, [ДЭА]ст, [ТЭА]ст, [NH3]ст, произведя замену переменных: [ОЭ] = [ОЭ]ст + [оэ], [МЭА] = [МЭА]ст + [мэа], [ДЭА] = [ДЭА]ст + [дэа], [ТЭА] = [ТЭА]ст + [тэа], где концентрации компонентов представлены как суммы их значений в стационарном состоянии и малых отклонений. Тогда математическая модель реактора-смесителя можно записать в виде
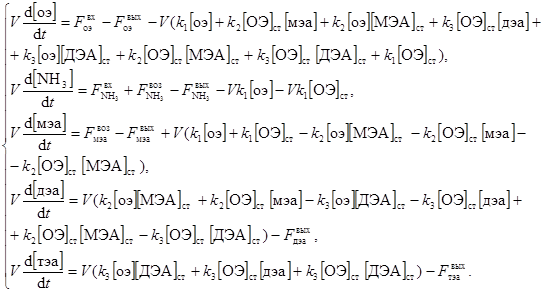
или
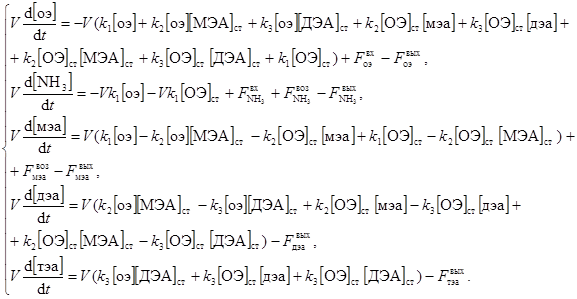
Если ввести следующие обозначения коэффициентов при переменных в системе

то представление модели будет более наглядным, а именно
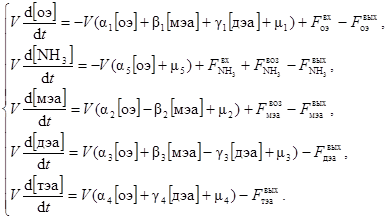
В данной модели представлены параметры состояния системы, входные и выходные факторы. Свойства многомерной системы можно исследовать, если представить ее описание уравнениями состояния и уравнениями выхода. Уравнения выхода можно получить из материального баланса объекта управления. Общий материальный баланс смесителя
![]()
входящий поток в РС, м3/ч,
![]()
выходящий поток из РС, м3/ч.
Отсюда можно получить уравнение выхода

а затем уравнения состояния
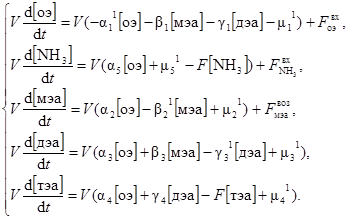
Здесь
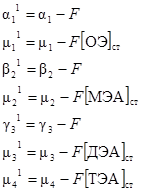
Многомерная система, описываемая уравнениями состояния и уравнениями выхода, полностью характеризуется набором трех матриц – A, B, C
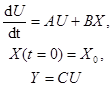
где U – вектор параметров состояния U([оэ], [мэа], [дэа], [тэа], [NH3]);
X – вектор входных параметров (управления) ![]() ;
;
Y – вектор выходных параметров ![]() .
.
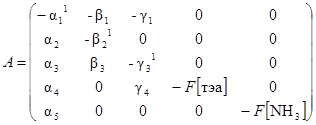
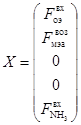
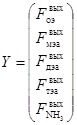
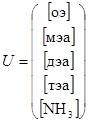
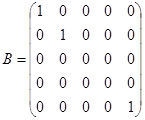
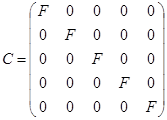
Система называется вполне управляемой по состоянию, если существует управляющее воздействие, которое может за конечный промежуток времени перевести систему из любого начального состояния U0 в любое заданное конечное состояние Uк.
Критерий управляемости по состоянию: для того чтобы система была вполне управляемой по состоянию, необходимо и достаточно, чтобы ранг матрицы управляемости по состоянию
W = [B AB A2B …]
равнялся размерности вектора состояния rangW = n.
Для исследуемой системы n = 5. Матрица W в данном случае может быть получена следующим образом
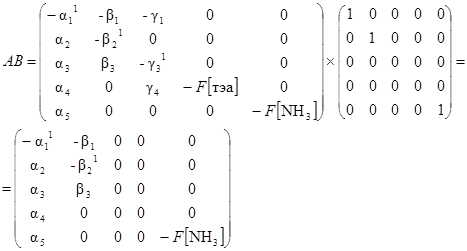
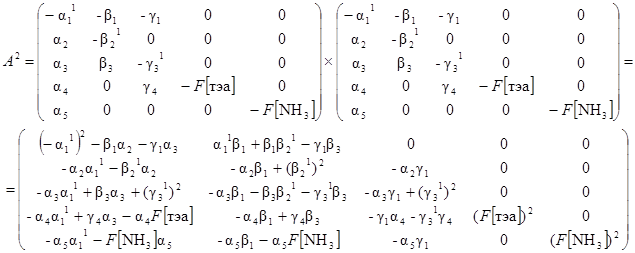
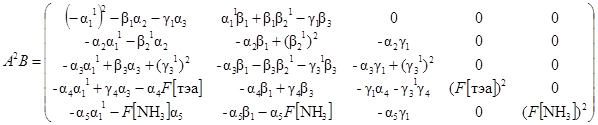
Присоединенная матрица W тогда может быть записана в виде
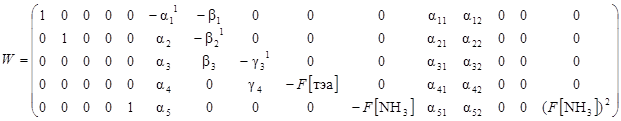
Данная матрица содержит не нулевой минор размера 5 × 5
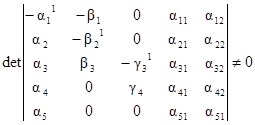
следовательно, ранг данной матрицы rangW = 5, и исследуемый объект является вполне управляемым по состоянию.
Система называется вполне управляемой по выходу, если выбором управляющего воздействия X(t) за конечный промежуток времени можно перевести систему из любого начального состояния в такое конечное состояние, которое обеспечивает заданное значение выхода.
Критерий управляемости по выходу: для того чтобы система была управляемой по выходу, необходимо и достаточно, чтобы ранг матрицы управляемости по выходу
P = [CB CAB …]
равнялся размерности вектора выхода rangP = k.
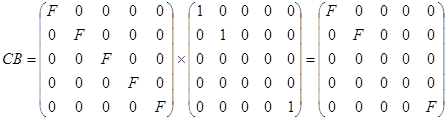
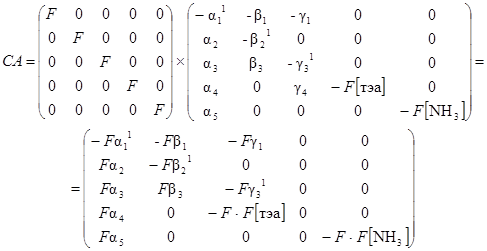
Затем получаем следующую матрицу
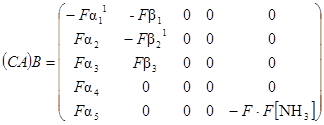
И наконец матрица управляемости по выходу
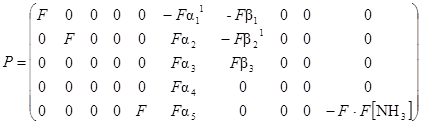
Имеется нулевой минор данной матрицы
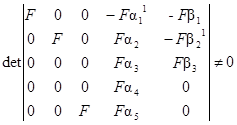
Наибольший ненулевой минор этой матрицы имеет размер 5 × 5, rangP = 5 и размерность вектора выхода равна 5. Следовательно, система является вполне управляемой по выходу.
Доказано, что системы, вполне управляемые по состоянию и выходу, являются и асимптотически устойчивыми.
Таким образом, исследование свойств объекта управления показывает, что система является вполне управляемой по состоянию и по выходу, а также асимптотически устойчивой.
Рецензенты:
Никандров И.С., д.т.н., профессор, профессор кафедры «Автомобильный транспорт и механика» ФГБОУ ВПО «Дзержинский политехнический институт (филиал) Нижегородского государственного технического университета имени Р.Е. Алексеева», Министерство образования РФ, г. Дзержинск.
Сидягин А.А., д.т.н., профессор, профессор кафедры «Машины и аппараты химического и пищевого производств» ФГБОУ ВПО «Дзержинский политехнический институт (филиал) Нижегородского государственного технического университета имени Р.Е. Алексеева», Министерство образования РФ, г. Дзержинск.
Библиографическая ссылка
Пенкин К.В. ИССЛЕДОВАНИЕ УПРАВЛЯЕМОСТИ И УСТОЙЧИВОСТИ СИСТЕМЫ УПРАВЛЕНИЯ СТАДИЕЙ СИНТЕЗА ЭТАНОЛАМИНОВ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11765 (дата обращения: 03.03.2026).



