Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шлычков С.В. 1

---

1 ФБГОУ ВПО «Поволжский Государственный технологический университет»

В работе рассматривается тонкостенная панель, закрепленная на относе от жесткого основания. Исследуется ее динамическое поведение как связанной упруго-акустической системы. Упругая система представляется прямоугольной панелью – шарнирно-опертой конструкцией из древесины. В качестве акустической системы рассматривается воздушный объем, заключенный между панелью и жестким основанием. Математическая модель строится с помощью метода конечных элементов. Для расчета низших собственных частот и форм колебаний используется метод итераций в подпространстве собственных векторов. Определяется и сопоставляется спектр колебаний парциальных и связанной динамических систем в диапазоне низших и средних частот. Установлено, что наличие воздушного промежутка между панелью и жестким основанием увеличивает количество резонансных частот упругой системы и позволяет более эффективно поглощать энергию звуковых колебаний в диапазоне низших и средних частот.

Статья в формате PDF

1112 KB

акустические свойства

метод конечных элементов

спектр собственных частот

акустическая панель

1. Акустика: Справочник/ А.П. Ефимов, А.В. Никонов, М.А. Сапожков, В.И. Шоров; Под ред. М.А. Сапожкова. – М.: Радио и связь, 1989. – 336 с.

2. Ашкенази Е.К., Ганов Э.В. Анизотропия конструкционных материалов. – Л.: Машиностроение, 1980. – 247 с.

3. Борисов Л.А, Градов В.А., Щиржецкий Х.А. Исследование акустических характеристик панелей, изготовленных из резонансной ели// Academia. Архитектура и строительство. – 2010, №3, – С. 85-90.

4. Ковригин С.Д., Крышов С.И. Архитектурно-строительная акустика. – М.: Высшая школа, 1985. – 256 с.

5. Колесников А.Е. Шум и вибрация: Учебник. - Л.: Судостроение, 1988. – 248 с.

6. Кузнецов Л.А. Акустика музыкальных инструментов: Справочник. М.: Легпромбытиздат, 1989. – 368 с.

7. В. Рейхардт. Акустика общественных зданий. – М.: Стройиздат, 1984. – 200 с.

8. Шлычков С.В. Особенности динамического поведения связанных систем/ Проблемы нелинейной механики деформируемого твердого тела: Тр. Второй междунар. конф. Казань, 8-11 декабря 2009 г. – Казань: Казан. Гос. ун-т, 2009. – С. 435-438.

9. Шлычков С.В. Исследование динамических процессов в задачах сопряженного типа// Ansys Advantage. Русская Редакция. – 2011, №2, Вып.16 – С. 43-49.

10. Шлычков С.В. Исследование динамических свойств связанных систем// Вестник Нижегородского университета им. Н.И. Лобачевского. – 2011, №4, часть 4 – С. 1873-1875.

Введение

Известно, что деревянные панели широко используются в отделке помещений. В случае их использования для корректировки тембра издаваемых звуков, подобные конструкции называют акустическими панелями [3]. В работе рассматривается панель, которая крепится к потолку или стенам помещений. Под действием звуковых волн панель начинает вибрировать, при этом максимальная интенсивность этих колебаний будет при совпадении собственных и вынужденных частот (явление резонанса). Вблизи панели, при этом, образуется звуковое поле, в котором происходит перераспределение энергии от одной полуволны колеблющейся конструкции к другой и обратно. В результате энергия звуковых волн не излучается в окружающее пространство, а остается «связанной» с панелью в виде кинетической энергии присоединенной массы некоторого объема воздушной среды, прилегающей к конструкции. Таким образом, осуществляется процесс звукопоглощения в диапазоне низших частот [1, 4]. Однако, начиная с некоторой граничной частоты, может начаться достаточно эффективное звукоизлучение от самой панели, что может негативно повлиять на акустику помещений. Величина этой частоты определяется формулой [5]:

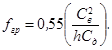(1)

Здесь Св – скорость звука в воздухе, Сд – скорость звука в древесине панели, h – толщина панели. На этой частоте длина изгибной волны становится равной длине звуковой волны и происходит волновое совпадение, при котором интенсивность изгибных колебаний резко увеличивается. Скорость звука в древесине определяется формулой [6]:

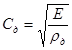, (2)

где E – модуль упругости вдоль волокон древесины, ρд – плотность древесины.

В строительной акустике качество акустических панелей принято оценивать двояко:

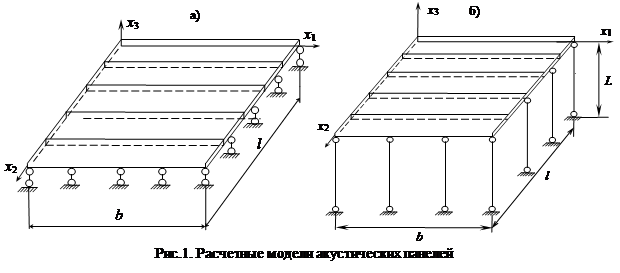
1. Исследование спектра собственных частот панели (рис.1, а).

Известна зависимость, позволяющая определять спектр частот для однородных шарнирно-опертых прямоугольных пластин [3]

(3)

Здесь – m, n = 1, 2, 3, … - числа натурального ряда; b и l - геометрические размеры пластины.

2. Определение низшей частоты упругой системы, состоящей из панели на относе от жесткого основания и упругого акустического объёма, заключенного между панелью и жестким основанием – стена или потолок (рис.2).

Известна эмпирическая зависимость, оценивающая низшую резонансную частоту, упругой системы [5].

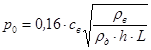(4)

Здесь ρд – плотность древесины, L – расстояние от панели до жесткого основания. При этом формула (4) получена исходя из предположения о геометрической однородности и изотропии конструкционного материала панели. Таким образом, в большинстве случаев, подобная оценка не может являться корректной.

Цель работы

Следовательно, возникает необходимость разработки методики расчета динамического поведения акустической панели, учитывающей влияние анизотропии конструкционных материалов и воздушной полости. Очевидно, для эффективной корректировки акустической характеристики помещения в низкочастотном диапазоне необходимо создание такой конструкции, которая имела бы максимально большое количество собственных частот (плотный спектр), лежащих ниже граничной частоты (1). Это позволило бы наиболее эффективно поглощать энергию звуковых колебаний в диапазоне низших частот.

Расчетные модели упругой и акустической систем

Акустическая панель представляется в виде шарнирно-опертой прямоугольной пластины, изготовленная из дощечек древесины ели, склеенных между собой вдоль волокон. Доски уложены вдоль короткой стороны. Толщина панели составляет h = 28 мм, длина l = 1500 мм, ширина b = 800 мм (рис.1, а). Координата x1 соответствует направлению вдоль волокон древесины, x2 – радиальному направлению, x3 – тангенциальному. Древесина представляется на основании модели ортотропного тела. Физико-механические характеристики древесины выбираются согласно [2]. Задача динамики решается методом конечных элементов (МКЭ) и описывается системой обыкновенных дифференциальных уравнений

[M]{}+ [K]{q}=0. (5)

(6)

Здесь [M], [K] – матрицы масс и жесткости конструкции; [Mf], [Kf] – матрицы масс и жесткости воздушного объема, заключенного между панелью и жесткой стенкой (рис.1, б).

Конечно-элементные соотношения, содержащие аппроксимирующие функции для давления (P) и перемещения (u), записываются в следующем виде

(7)

(8)

Здесь – вектор узловых давлений, – вектор узловых перемещений, и – функции формы для давления и перемещения акустического КЭ соответственно.

Для дискретизации пластины используются шестиузловые оболочечные конечные элементы (КЭ) Shell 93 с 6 степенями свободы в узле. Для дискретизации воздушной полости - объемные акустические КЭ Fluid 30. Рассмотрен режим свободных колебаний шарнирно-опертых по контуру акустических панелей и воздушного объема с размерами bXlXL. Результаты решений уравнений (5) и (6) на собственные значения сведены в табл. 1.

Расчетная модель связанной упруго-акустической системы

В матричной форме с учетом МКЭ волновое уравнение уравнение, составленное для связанной упруго-акустической системы будет иметь вид

. (9)

Здесь ρ – добавленная матрица масс, учитывающая взаимодействие между граничными КЭ акустической полости и КЭ структуры.

При этом

, (10)

где – это вектор направляющих косинусов нормали к поверхности панели, взаимодействующей с акустической средой, A – площадь панели.

Уравнения движения для КЭ модели панели записываются в виде

. (11)

Здесь - вектор нагрузок, инициируемых давлением со стороны акустической полости на поверхность панели, определяется формулой:

, (12)

Учитывая формулировку (12), уравнения динамики акустической полости (6) и структурной модели (11) в связанной постановке запишутся в виде [12]

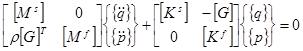. (13)

Динамический анализ связанной упруго-акустической системы

Под связанной будем понимать систему (CC), состоящую из двух или более сопряженных областей. При этом для любого момента времени поведение одной системы оказывает влияние на поведение другой и наоборот [8-10]. Анализ проведенных численных исследований для панели с учетом упругости воздушного объема, находящегося между ней и жестким основанием на расстоянии L = 250 мм (рис.1, б), позволил систематизировать полученные результаты в табл. 1. Здесь представлены частоты, находящиеся в акустически важном диапазоне частот до граничной частоты, определяемой по формуле (1). Для расчета граничной частоты принята Св =340 м/c; согласно данным [2] по формуле (2) скорость звука вдоль волокон древесины ели получается Сд = 5697 м/c. Согласно (1) величина граничной частоты = 403 Гц. Для идентификации форм колебаний используются буквенные обозначения m, n, k – количество полуволн в направлениях x1, x2, x3.

Таблица 1. Спектр колебаний

Видно существенное (15%) повышение величины низшей собственной частоты для СС при повторении структурной моды парциальной системы. Сопоставление низших форм колебаний представлено на рис.2 и рис.3. При этом структурные и акустические моды CC повторяют моды парциальных систем, которые имеют место в данной частотной области: 2, 3 и 4 собственные частоты СС реагируют по первой акустической моде воздушного объема, 5 и 7 – по второй (рис.2). Структурные формы колебаний также накладываются на акустические моды (рис.3). Взаимодействуя друг с другом, они меняют спектр колебаний СС, делают его качественно (p9 на рис.3) и количественно (табл.1) другим.

Заключение

На базе МКЭ разработана расчетная модель акустической панели на относе от жесткого основания, как связанной упруго-акустической системы. Результаты расчета заметно отличаются от данных, полученных посредством известных соотношений (3) и (4). Установлено, что спектр колебаний СС отличается от парциальных в диапазоне низших частот незначительно.

Рис.2. Акустические моды – поля распределений давления на резонансных частотах воздушного объема и СС

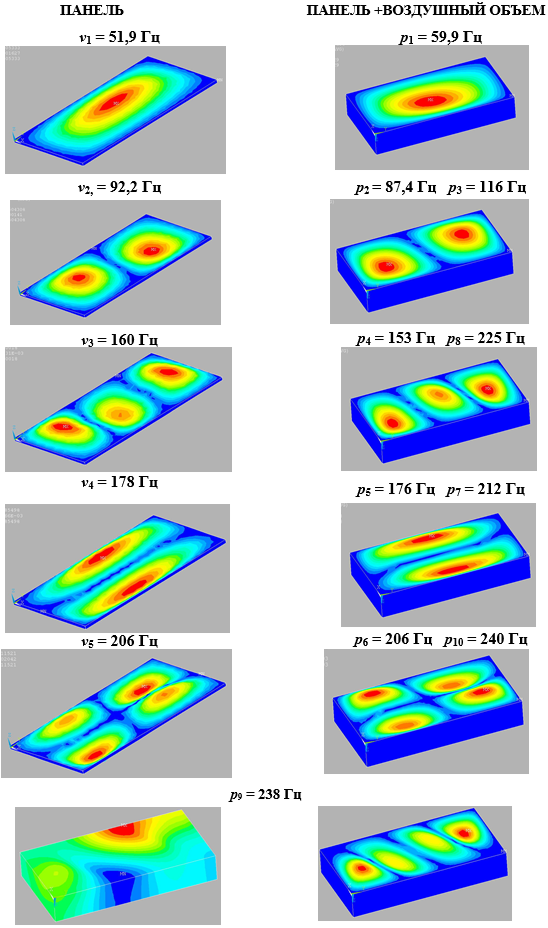
Рис.3. Формы колебаний панели и СС

В диапазоне средних частот выявлены новые устойчивые режимы колебаний для СС и соответственно новые частоты и формы колебаний, существенно отличающиеся от парциальных систем. Структурные моды, находящиеся в этих частотных областях гасятся или видоизменяются. В полосе более высоких частот они вообще перестают реализовываться.

Наличие воздушного промежутка между панелью и жестким основанием увеличивает количество резонансных частот упругой системы и позволяет более эффективно поглощать энергию звуковых колебаний в диапазоне низших и средних частот.

Работа выполнена при поддержке гранта РФФИ №13-01-97045 р_поволжье_а

Рецензенты:

Иванов С.П., д.т.н., профессор, зав. кафедрой «Сопротивления материалов и прикладной механики» ФГБОУ ВПО «ПГТУ», г. Йошкар-Ола.

Куликов Ю.А., д.т.н., профессор кафедры «Сопротивления материалов и прикладной механики» ФГБОУ ВПО «ПГТУ», г. Йошкар-Ола.

Библиографическая ссылка