
В современной химической отрасли промышленности предъявляются повышенные требования к герметичности крупногабаритного оборудования, что связано с наличием в них большого количества взрывопожароопасных и токсичных веществ. Нормативными документами устанавливаются требования по проведению процедуры контроля герметичности, заключающейся в обследовании всех имеющихся в таких изделиях сварных швов, в частности методами течеискания. Однако имеющиеся методы неразрушающего контроля течеисканием являются неэффективными при большой протяжённости швов, так как имеют высокий уровень трудозатрат и плохо поддаются автоматизации [3].
Для повышения эффективности процедуры контроля был предложен вакуумно-камерный способ течеискания, основанный на накоплении утечки пробного газа (ПГ) в пористой среде, размещённой в подвижной вакуумной камере. На основе этого способа было разработано устройство локализации течей (ЛТ) [2], состоящее из накопительной пористой мембраны с газонепроницаемой верхней гранью и датчика потока (давления) пробного газа (рис. 1).
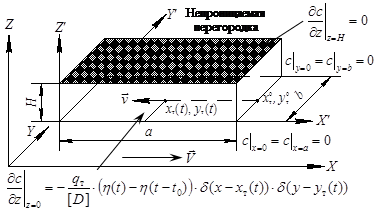
Рис. 2. К выводу математической модели переноса газа в случае подвижной пористой мембраны.
В условиях испытания на герметичность в устройстве происходит нестационарный массоперенос в пористой среде. Для описания данного процесса получена математическая модель:
![]() (1)
(1)
![]() (2)
(2)
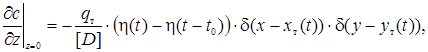
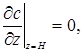 (3)
(3)
![]() (4)
(4)
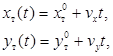 (5)
(5)
где e — пористость материала; ![]() — коэффициент эффективной кнудсеновской диффузии;
— коэффициент эффективной кнудсеновской диффузии; ![]() — концентрация ПГ в пористой мембране;
— концентрация ПГ в пористой мембране; ![]() — фоновая концентрация ПГ в вакуумной камере;
— фоновая концентрация ПГ в вакуумной камере; ![]() — координаты точки в пористом теле; a, b, H — размеры пористого тела;
— координаты точки в пористом теле; a, b, H — размеры пористого тела; ![]() — поток ПГ через течь;
— поток ПГ через течь; ![]() — текущие координаты течи;
— текущие координаты течи; ![]() — дельта-функция Дирака; D — оператор Лапласа;
— дельта-функция Дирака; D — оператор Лапласа; ![]() — единичная функция Хевисайда,
— единичная функция Хевисайда, ![]() — время перемещения ЛТ над течью (или время движения течи непосредственно под пористой мембраной);
— время перемещения ЛТ над течью (или время движения течи непосредственно под пористой мембраной); ![]() — координаты течи в начальный момент времени;
— координаты течи в начальный момент времени; ![]() — проекции вектора скорости ЛТ
— проекции вектора скорости ЛТ ![]() на оси координат
на оси координат ![]() (рис. 2).
(рис. 2).
При выводе модели были сделаны следующие допущения:
- используется квазигомогенное приближение — феноменологический подход, при котором уравнения для массопереноса в сплошной среде переносятся на процессы при свободно-молекулярном режиме течения газа [4];
- вне пористого тела поддерживается постоянное разряжение, а флуктуация фоновой концентрации ПГ мала, и можно считать, что
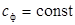 ;
; - функция источника
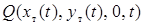 действует в области W;
действует в области W; - движение ЛТ является прямолинейным с постоянной скоростью v;
- коэффициент эффективной диффузии и релаксационный коэффициент эффективной диффузии равны, что позволяет говорить только об одном коэффициенте эффективной кнудсеновской диффузии
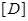 . Дополнительно примем, что в процессе массообмена
. Дополнительно примем, что в процессе массообмена 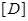 изменяется незначительно;
изменяется незначительно; - используя принцип относительности Галилея, примем за неподвижную систему координат
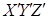 (связанную с вакуумной камерой) и будем считать, что движется течь (источник).
(связанную с вакуумной камерой) и будем считать, что движется течь (источник).
Решение указанной модели было получено методом функций Грина [5]:
![]() (6)
(6)
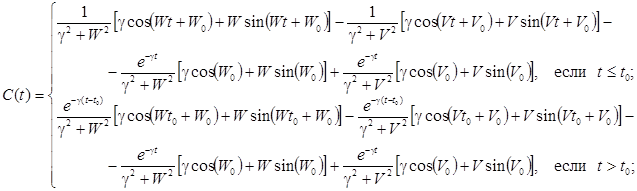
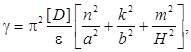 (7)
(7)
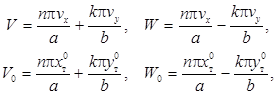
Компьютерное моделирование в среде LabVIEW позволяло получить картину эволюции концентрационного поля утечки пробного газа (рис. 3). На графиках концентрация выражена в единицах давления (Па).
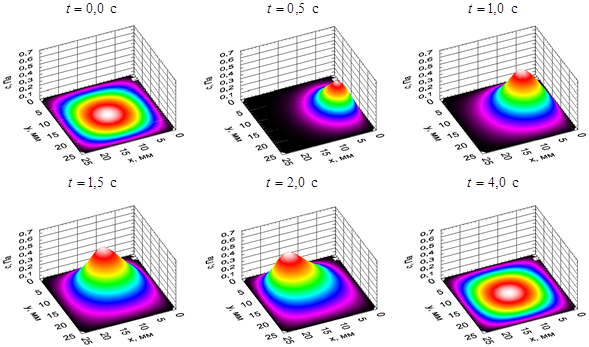
Рис. 3. Эволюция концентрационного поля утечки пробного газа в плоскости ![]() .
.
Параметры моделирования: ![]() м,
м, ![]() м,
м, ![]() м,
м,
![]() м3×Па/с,
м3×Па/с, ![]() м2/с,
м2/с, ![]() м/с.
м/с.
В начальный момент времени распределение ПГ обусловлено фоновой составляющей. При дальнейшем развитии временно́го процесса в распределении КПУПГ можно выделить первоначальную стадию накопления ПГ в поровом пространстве (приблизительно до 2-й секунды) и дальнейший релаксационный процесс, связанный с освобождением пористой структуры от накопленного ПГ (![]() с).
с).
Усреднив концентрацию по всей верхней грани пористого материала (непосредственно под непроницаемым слоем), получим следующий график зависимости средней концентрации ![]() от времени (рис. 4). Данный график является моделью дефектоскопического сигнала, полученного от устройства локализации течей.
от времени (рис. 4). Данный график является моделью дефектоскопического сигнала, полученного от устройства локализации течей.
а)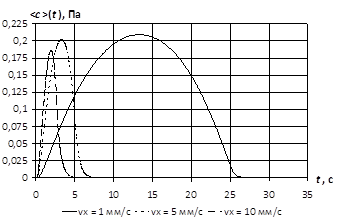
б)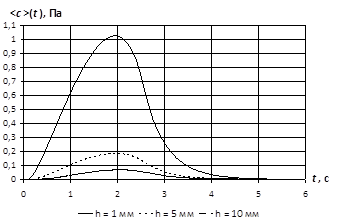
Рис. 4. Зависимость средней концентрации (в ед. давления) на верхней грани пористого материала при зависимости
а) — от скорости перемещения ЛТ;
б) — от толщины пористой мембраны.
Аналитическое решение
(6) — (7) математической модели (1) — (5) позволяет выявить характер влияния конструктивных (геометрические размеры датчика утечки) и режимных параметров (скорость перемещения) на порог чувствительности устройства локализации течей, быстродействие и достоверность контроля.
Для анализа дефектоскопической информации был разработан алгоритм [1], основанный на цифровой обработке сигнала в среде разработки виртуальных приборов NI LabVIEW. Данный алгоритм позволяет с помощью программно-аппаратных средств сделать заключение о достоверности дефектоскопической информации, а проводимый в ходе работы программы анализ параметров дефектоскопического сигнала позволяет определять такие параметры течи, как поток ПГ через нее и ее положение относительно траектории.
Указанное устройство может быть использовано в составе высокоэффективных систем контроля герметичности в автоматизированном (в том числе, дистанционном) режиме.
Рецензенты:
Луконин В.П., д.т.н., профессор, генеральный директор ФГУП «НИИ полимеров им. академика В.А. Каргина», г. Дзержинск.
Добротин С.А., д.т.н., профессор, профессор кафедры математики и естественно-научных дисциплин ФГОУ ВПО «Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации, Дзержинский филиал», г. Дзержинск.
Библиографическая ссылка
Костиков Е.С., Лобаев А.Н., Малыгин А.Л., Мясников В.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УСТРОЙСТВА ЛОКАЛИЗАЦИИ ТЕЧЕЙ В КРУПНОГАБАРИТНЫХ ИЗДЕЛИЯХ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11040 (дата обращения: 13.02.2026).



