Предотвращение разрушения лопаток от многоцикловой усталости – одна из важнейших задач, решаемых при проектировании и доводке газотурбинных двигателей. Традиционный подход к оценке динамической прочности лопаток апробирован многолетней практикой и в целом позволяет обеспечить прочностную надежность лопаток. Тем не менее при доводке и эксплуатации двигателей наблюдаются поломки лопаток, до 70-80% которых, по данным [1; 9], имеют усталостное происхождение. Отчасти они являются следствием неполного учета внешних воздействий и реальных условий эксплуатации, таких как повреждение посторонними предметами, попадающими в проточную часть двигателя [5-8; 10]. В силу случайной природы источников возбуждения колебаний лопаток, рассеяния их размеров, демпфирования, амплитуды колебаний лопатки и вибронапряжения имеют значительный разброс - даже на лопатках одного рабочего колеса он может быть трехкратным и более [1].
Основным направлением обеспечения сопротивления лопаток разрушению от многоцикловой усталости является отстройка от резонансных колебаний. Она обеспечивается, в частности, соответствующим выбором размеров пера лопатки. Рассеяние этих размеров в пределах допусков на изготовление приводит к рассеянию собственных частот колебаний лопаток, что в свою очередь может привести к резонансным явлениям и усталостным поломкам. Допуски назначаются на основании требований аэродинамики, технологических возможностей, опыта доводки и эксплуатации двигателей. Такая практика в целом себя оправдывает, однако имеют место случаи, когда допуски оказываются недостаточными для исключения резонансных колебаний. С другой стороны, в ряде случаев допуски устанавливаются необоснованно жесткими с точки зрения рассеяния собственных частот, что приводит к увеличению себестоимости производства. При назначении допусков необходимо, наряду с другими соображениями, учитывать влияние допусков на рассеяние собственных частот.
В настоящей работе исследование влияния отклонений размеров профильной части на рассеяние низшей собственной частоты изгибных колебаний проведено на примере рабочей лопатки 2-й ступени компрессора низкого давления.
Исследуемая лопатка (рис. 1а) имеет замок типа «ласточкин хвост» и профильную часть, ограниченную криволинейными поверхностями. Геометрия поверхностей спинки и корыта задается в нескольких поперечных сечениях хордой b , толщиной Cmax и кривизной сечения h. Лопатки изготовлены из титанового сплава ВТ8М с модулем упругости E=1,15×![]() МПа, и плотностью r=4480 кг/м3. Рассеяние размеров профильной части лопатки регламентируется допуском D на отклонение от номинала формы контура корыта и спинки в нескольких сечениях. Допуск D состоит из двух составляющих: на утолщение D1 и «в тело» D2 (рис. 1б).
МПа, и плотностью r=4480 кг/м3. Рассеяние размеров профильной части лопатки регламентируется допуском D на отклонение от номинала формы контура корыта и спинки в нескольких сечениях. Допуск D состоит из двух составляющих: на утолщение D1 и «в тело» D2 (рис. 1б).
а)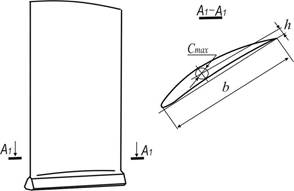 б)
б)
Рисунок 1 – Исследуемая лопатка (а) и схема задания допусков на отклонение от номинала формы контура корыта и спинки (б)
а) 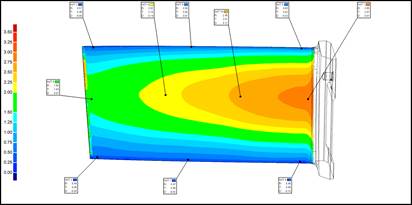 б)
б)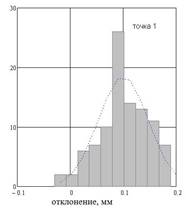
Рисунок 2 - Пример сравнения результатов оцифровки лопаток с твердотельной моделью (а) и гистограмма распределения отклонений от номинала максимальной толщины профиля в корневом сечении (б)
Для определения статистических характеристик рассеяния размеров реальных лопаток была произведена оцифровка партии из 99 лопаток с помощью оптической системы ATOSII. В результате были получены цифровые копии лопаток, которые сравнивались с CAD-моделью в системе Geomagic Qualify. Результатами оцифровки являются цветовые карты отклонений оцифрованной лопатки от CAD-модели (рис. 2а). Проведено сравнение результатов оцифровки с твердотельной моделью, получены результаты измерения толщины профиля в 10 характерных точках. На рис. 2б приведена в качестве примера гистограмма распределения отклонений от номинала значений максимальной толщины профиля в корневом сечении пера лопатки. В этом и других сечениях распределение отличается от нормального, медиана смещена в область положительных отклонений, то есть лопатки в среднем более «толстые», чем предусмотрено чертежом.
Для оценки рассеяния низшей собственной частоты колебаний лопатки использовали простейшую стержневую модель, основанную на предположении об одноосном напряженном состоянии лопатки и гипотезе плоских сечений. Такие модели пригодны для приближенной оценки низшей собственной частоты изгибных колебаний лопатки [2]. Лопатка рассматривается как консольно закрепленный стержень с переменными по длине (координата x) площадью сечения F(x) и моментом инерции I(x), зависящими от геометрических параметров сечения b , Cmax и h (рис. 1а). При заданной приближенно первой изгибной собственной формы колебаний y0(x) собственная частота f1 определяется энергетическим методом как [2]:
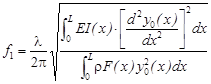 , (1)
, (1)
где l - коэффициент, учитывающий влияние податливости закрепления.
Так как отклонения размеров лопатки от номинальных значений являются случайными величинами, собственная частота колебаний также является случайной величиной. В рамках статистического подхода она описывается законом распределения, а ее статистическими характеристиками являются параметры этого распределения. Для их определения используется метод статистического моделирования (Монте-Карло), суть которого состоит в многократном повторении расчета собственной частоты (1) при случайных сочетаниях размеров лопатки в рамках допусков и последующей статистической обработке полученного множества случайных значений частоты.
Основными параметрами, определяющими разброс низшей собственной частоты колебаний лопатки, являются отклонения от номинала значений толщины и кривизны профиля. Эти отклонения не являются независимыми случайными величинами. Они связаны с отклонениями формы контуров спинки и корыта от теоретического профиля D1 и D2, которые непосредственно регламентируются в конструкторской документации. Конкретными варьируемыми параметрами в каждом сечении являются расстояния от хорды до наиболее удаленной точки контура корыта yк и до наиболее удаленной точки контура спинки yc. Максимальная толщина и кривизна профиля рассчитываются через эти величины как:
Cmax= yc - yк , h=( yc + yк) /2 . (2)
Параметры yc и yк варьируются в пределах одинаковых допусков D=D1+D2
Рассматривались два случая распределения случайных величин yc и yк в пределах допуска D - нормальное и равномерное.
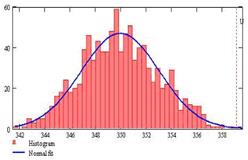
Рисунок 3 - Пример расчетной гистограммы распределения собственной частоты
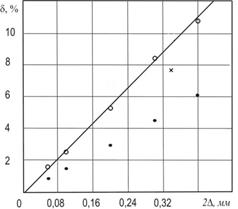
Рисунок 4 - Зависимости параметра рассеяния низшей собственной частоты от суммарного допуска D: о - стержневая модель, метод Монте-Карло, равномерное распределение отклонений размеров, ● - стержневая модель, метод Монте-Карло, нормальное распределение отклонений размеров, х - экспериментальные данные
Расчеты методом статистического моделирования проводили для различных значений допуска D и различных соотношений D1 и D2 при двух различных вариантах законов распределения yc и yк. В результате каждого расчета получена выборка из 1000 случайных значений собственной частоты, которая характеризуется средним значением fср , среднеквадратическим отклонением sf , коэффициентом вариации K=sf /fср. Рассеивание собственной частоты дополнительно оценивали параметром
![]() . (3)
. (3)
Полученные распределения собственной частоты близки к нормальному. На рис. 3 приведен пример полученной методом статистического моделирования гистограммы распределения собственной частоты колебаний для равномерного распределения отклонений толщины при D1/D2= 1,5, D=0,1 мм.
На рис. 4 показаны полученные в результате статистического моделирования зависимости параметра рассеяния частоты d от величины допуска D для двух вариантов распределения размеров в пределах допуска: равномерного и нормального. Оказалось, зависимости d(D) слабо зависят от отношения D1/D2 и описываются линейным соотношением:
d = А.D , (4)
где А - константа, зависящая от формы и размеров лопатки. Для исследованных лопаток она составила 53%/мм для равномерного распределения отклонений размеров лопаток в пределах допуска и 31,5%/мм для нормального распределения.
Проведено экспериментальное исследование рассеяния собственных частот изгибных колебаний исследуемых лопаток, цель которого состояла в проверке полученных статистическим моделированием данных. Исследована партия из 25 лопаток. По результатам оцифровки лопаток с помощью оптической системы ATOSII получено отклонение толщины профильной части от номинала в пределах 2D=0,35 мм.
Частоты и формы колебаний лопаток определялись методом сканирующей лазерной виброметрии с использованием аппаратно-программного комплекса Polytec 400-3D по методике, описанной в [3; 4]. Исследуемые лопатки крепили консольно в замке пружинного типа, который устанавливался в массивное прецизионное зажимное устройство и затягивался заданным усилием. Возбуждение колебаний лопатки при испытаниях осуществлялось акустическим способом с помощью динамической головки 3ГДШ-2. Сетка сканирования состояла из 153 точек, число измерений при осреднении устанавливалось равным 5.
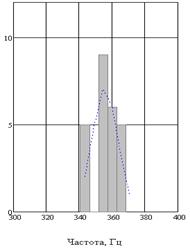
Рисунок 5 - Гистограмма распределения низшей собственной частоты колебаний, построенная по экспериментальным данным
Перед проведением основной группы экспериментов были проведены вспомогательные эксперименты, цель которых состояла в том, чтобы оценить рассеяние собственных частот в связи с вариацией условий контакта в замке при закреплении лопатки. Одна из лопаток закреплялась в зажимном устройстве с заданным усилием, и производилось определение собственных частот. Процедура установки, затяжки и измерения повторялась 6 раз. Рассеяние собственных частот оценивалось параметром d. Его значение для низшей собственной частоты составило 0,6%.
Результаты экспериментального исследования исследуемой партии лопаток приведены в виде гистограммы распределения низшей собственной частоты колебаний на рис. 5. Среднее значение частоты составило 355,5 Гц, среднее квадратическое отклонение 7,7 Гц, коэффициент вариации 2,2%, параметр рассеяния d= 7,7%. Это – значительно больше полученных выше значений, характеризующих воспроизводимость закрепления лопаток.
На рис. 4 приведено сравнение полученного экспериментально значения d с расчетным, полученным методом статистического моделирования. Видно, что расчетные и экспериментальные данные согласуются с результатами расчета для равномерного распределения размеров в пределах допуска, расхождение лежит в пределах 17%. Для расчетов, проведенных в предположении нормального распределения, расхождение с экспериментальными данными существенно больше – в 1,5 раза.
Разработанная методика и полученные результаты могут быть использованы при обосновании допусков на отклонение от номинала размеров профильной части лопаток с точки зрения отстройки от резонансных режимов.
Работа выполнена при финансовой поддержке Минобрнауки РФ (договор № 02.G25.31.0016) в рамках реализации Постановления Правительства РФ № 218 «О мерах государственной поддержки развития кооперации российских высших учебных заведений и организаций, реализующих комплексные проекты по созданию высокотехнологичного производства».
Рецензенты:
Бульбович Р.В., д.т.н., декан аэрокосмического факультета Пермского национального исследовательского политехнического университета, г. Пермь.
Карманов В.В., д.т.н., профессор, зав. кафедрой «Инновационные технологии машиностроения» Пермского национального исследовательского политехнического университета, г. Пермь.
Библиографическая ссылка
Нихамкин М.Ш., Воронов Л.В., Семенова И.В., Болотов Б.П., Головкин А.Ю. ВЛИЯНИЕ РАССЕЯНИЯ РАЗМЕРОВ ЛОПАТОК КОМПРЕССОРА НА РАССЕЯНИЕ СОБСТВЕННОЙ ЧАСТОТЫ ИЗГИБНЫХ КОЛЕБАНИЙ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=10687 (дата обращения: 03.03.2026).



