Введение
В современных условиях назрела необходимость формирования качественно новых методических подходов оценки эффективности инвестиций, учитывающих риски, а также неполноту и/или неточность исходной информации.
В настоящее время существуют различные подходы к оценке рисков. Особый интерес представляет теория нечеткой логики (fuzzy logic), определяющая современный подход к описанию бизнес-процессов, в которых присутствуют неопределенность и неточность исходной информации. В [3] рассмотрено применение формализма нечеткой логики к оценке эффективности инвестиций в информационные системы предприятия. Для описания проекта были выбраны следующие параметры: чистая текущая стоимость (NPV), внутренняя норма рентабельности (IRR), срок окупаемости проекта (РВ), учетная норма рентабельности (ARR), индекс рентабельности инвестиций (PI). Каждому параметру соответствовала нечеткая переменная с заданной функцией принадлежности. Значение выходной переменной определяло вероятность эффективности проекта. В [4] аналогичный алгоритм был применен к оценке эффективности инновационного проекта внедрения передвижных отделений почтовой связи (ПОПС) в Калужской области [1].
Одной из основных проблем применения нечеткой логики является выбор функций принадлежности нечетких переменных. Основными видами функций принадлежности являются треугольные, трапециевидные, кусочно-линейные, гауссовы, сигмоидные и другие функции. Заметим, что выбор функции принадлежности конкретной переменной представляет собой плохо формализованную задачу, решение которой основано на интуиции и опыте.
В настоящей работе рассмотрены примеры выбора функций принадлежности нечетких переменных. В качестве алгоритма нечеткой логики применялся алгоритм Мамдани [2]. В качестве среды реализации алгоритма был выбран пакет прикладных программ Mathcad. Детальное описание реализации алгоритмов нечеткой логики в Mathcad дано в [5, 6].
Примеры вычислений
Рассмотрим два примера выбора функции принадлежности для нечетких переменных срок окупаемости проекта РВ и индекс рентабельности инвестиций PI.
В [3] рассматривались инвестиции в информационные системы предприятия. Известно, что через три года начинается моральное старение информационных продуктов, а через 5 лет происходит смена поколения информационных продуктов. Поэтому можно выбрать следующие характеристики функции принадлежности:
- интервал изменения переменной PB равен 5;
- терм-множество нечеткой переменной {High (приемлемый), Low (неприемлемый)};
- функция принадлежности − трапециевидная с параметрами [0 0 3 5] (на рис. 1 показана реализация вычислений в Mathcad).
Из рис. 1 видно, что трапециевидные функции принадлежности задаются четырьмя точками, характеризующими трапецию. Кроме того, очевидно, что треугольную функцию принадлежности можно рассматривать как частный случай трапециевидной, у которой совпадают средние точки (на рис. 1 это точки с координатами (0, 1) и (3, 1)). Частным случаем трапециевидной функции является также ступенчатая функция принадлежности.
В [3] реализован более простой случай задания ступенчатой функции принадлежности переменной PB, которая имеет логическое значение «yes», если срок окупаемости проекта меньше пяти, и «no» – в противном случае.
В [4] мы рассмотрели два варианта задания базы правил.
В первом варианте считались допустимыми все проекты с положительным значением чистой приведенной стоимости:
- если NPV или IR низкий, то результат низкий;
- если NPV средний, IRR средний, PB = «yes», AR = «yes» и PI – высокий, то результат средний;
- отвергаются проекты со сроком окупаемости более трех лет или учетной нормой рентабельности менее 20 %. Здесь возможны два варианта: 1) данные проекты отвергаются в процессе предварительного анализа и не обрабатываются на основе нечеткой логики; 2) для переменных РВ и ARR задаются «ступенчатые» функции принадлежности, которые равны нулю на соответствующих интервалах;
- если PB и ARR имеют логическое значение «да» и PI – высокий, то результат высокий.
Во втором варианте последнее правило имело вид:
- если NPV высокий, а PB и ARR имеют значение «да» и PI – высокий, то результат высокий.
Очевидно, что первый вариант является более «мягким», а второй - более «жестким». Первый вариант основан на обычно используемом в учебниках по финансовой математике правиле о принятии проекта с положительной NPV. Во втором варианте предъявляются некоторые требования к значению NPV. Далее мы будем рассматривать вычисления именно по этому варианту.
Чтобы продемонстрировать влияние вида функций принадлежности, рассмотрим переменную PB с набором значений лингвистической переменной {«Низкий», «Высокий»} с трапециевидными функциями принадлежности с параметрами [0; 0; 1,5; 3] и [0; 0; 1,5; 3] соответственно. Значения «Низкий» и «Высокий» в данном случае говорят о приемлемости срока проекта для заказчика.
Исходя из результатов моделирования в Project Expert [1], мы выбрали интервал изменения переменной NPV от 0 до 2000 тыс. руб. Срок выполнения проекта менялся в интервале от 0 до 5 лет, значение индекса эффективности инвестиций – от 0 до 10. Зададим следующие значения входных переменных:
NPV = 1900; IRR = 12,5; PB = 2; ARR = 37; PI = 9 .
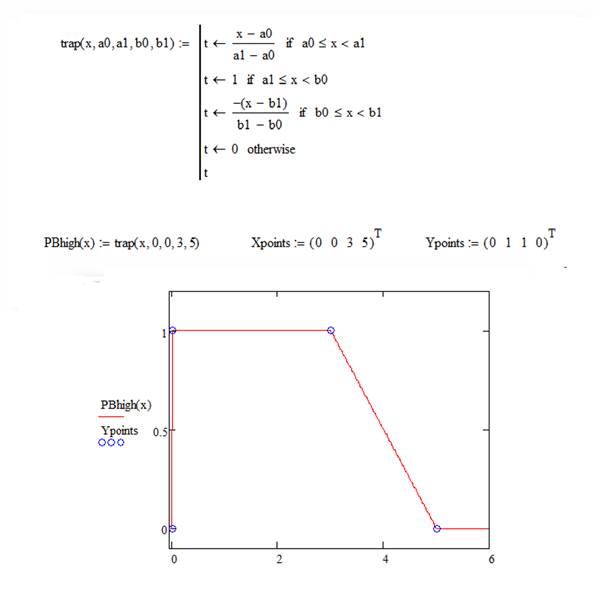
Рис. 1. Пример функции принадлежности для переменной PB
Интуитивно понятно, что данные значения должны соответствовать достаточно высокой эффективности проекта.
Результаты моделирования показаны на рис. 2. В данном случае предполагаемая вероятность эффективности проекта не превысила 60 %. Из рис. 2 видно, что это связано с тем, что при таком выборе функций принадлежности вклад функции «Низкий срок окупаемости» является достаточно весомым.
Заменим трапециевидные функции принадлежности на гауссовы с параметрами [0; 1,5] и [5; 1,5]. При этом область «перекрывания» функций значительно уменьшается, и вероятность эффективности проекта повышается до 70,9%.
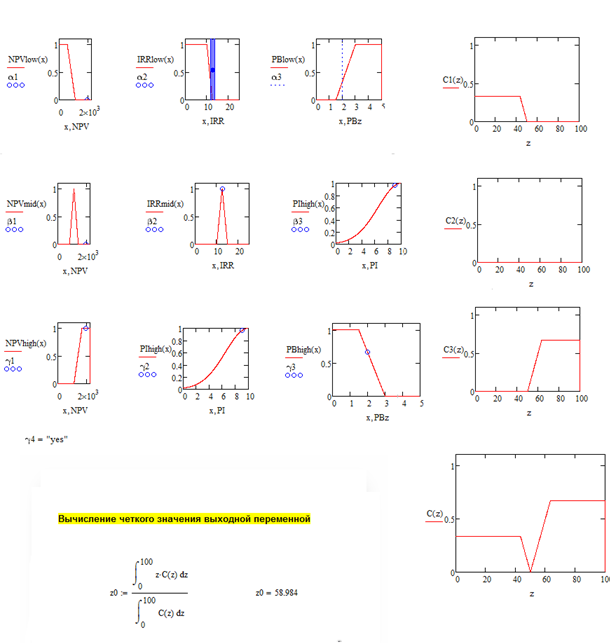
Рис. 2. Пример расчета эффективности инвестиций
Рассмотрим аналогично выбор функции принадлежности для переменной индекс рентабельности инвестиций PI [1, 2]. Предполагалось, что значение переменной изменяется в интервале [0, 10] и описывается терм-множеством {«Низкий», «Высокий»}. В [1] для оценки эффективности инвестиций в информационные системы предприятия предлагалось использовать трапециевидную функцию принадлежности с параметрами [0, 0, 5, 10] для нечеткой переменной «Низкий PI» и с параметрами [0, 5, 10, 10] для нечеткой переменной «Высокий PI». Однако расчеты показывают, что в этом случае значение PI слабо влияет на значение выходной переменной, т. к. трапеция является слишком «массивной» и вносит достаточно большой вклад даже при значении PI, близком к нулю. Например, при PI = 1 значение выходной переменной составляет ~65 %. Более реалистичные результаты получаются, если взять гауссовы функции принадлежности.
Заключение
Показано, что вид функции принадлежности может существенно влиять на результаты вычислений с использованием формализма нечеткой логики.
Методика подбора функций принадлежности рассмотрена на примерах оценки эффективности инвестиций в информационные системы и инновационные проекты.
Рецензенты:
Крутиков В.К., д.э.н., профессор, проректор по научно-методической работе НОУ ВПО «Институт управления, бизнеса и технологий», г. Калуга.
Обрубов Ю.В., д.ф.-м.н., профессор кафедры «Высшая математика» Калужского филиала ФГБОУ ВПО «Московский государственный технический университет имени Н. Э. Баумана», г. Калуга.
Библиографическая ссылка
Семененко М.Г., Князева И.В., Черняев С.И. ПРОБЛЕМЫ ВЫБОРА ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ НЕЧЕТКИХ МНОЖЕСТВ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10303 (дата обращения: 16.02.2026).



