Введение
В середине прошлого века теория транспортных потоков образовала самостоятельную ветвь в прикладной математике. Существует большое количество математических моделей, отличающихся по математическому аппарату и степени детализации, позволяющих решать различные задачи по распределению транспортных потоков внутри сети. Задачи макромоделирования базируются на поиске равновесного распределения потоков, микромоделирование решает проблемы пропускных способностей локальных участков сетей [2]. Из-за различного характера гипотез, закладываемых в макро- и микромодели, задача обмена информацией между ними не решена ни теоретически, ни в виде программных продуктов.
Эффективность решения задачи поиска потокового равновесия во многом зависит от способа аналитического задания функции транспортных затрат. Авторами в работе [3] предложена математическая модель транспортной сети, которая базируется на гипотезе о распределении интервалов по времени по обобщенному закону Эрланга.
Функция распределения обобщенного закона Эрланга
Согласно проведенным авторами исследованиям [5], распределение интервалов по времени между требованиями в транспортном потоке при интенсивности движения по одной полосе до 300 авт/ч хорошо согласуется с законом Эрланга. Однако в более плотных потоках расхождение между теоретическим и эмпирическим распределениями становится существенным. Ряд авторов [1,4] утверждает, что с помощью обобщенного закона Эрланга можно аппроксимировать практически любое распределение случайной величины.
Простым обобщением специального распределения Эрланга порядка ![]() является случай, при котором показательные распределения длительности
является случай, при котором показательные распределения длительности ![]() стадий имеют различные параметры
стадий имеют различные параметры ![]() . Преобразование Лапласа функции плотности такого распределения является рациональной функцией и имеет вид:
. Преобразование Лапласа функции плотности такого распределения является рациональной функцией и имеет вид:
![]() . (1)
. (1)
Для получения самой функции плотности распределения ![]() необходимо разложить (1) на простые дроби с помощью метода неопределенных коэффициентов и найти оригинал по его изображению. В случае, если все параметры
необходимо разложить (1) на простые дроби с помощью метода неопределенных коэффициентов и найти оригинал по его изображению. В случае, если все параметры ![]() различны, функция плотности имеет вид:
различны, функция плотности имеет вид:
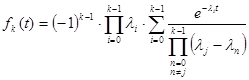 (2)
(2)
Если ввести следующие обозначения: 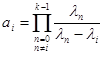 ,
, ![]() ,
,
то функция плотности распределения примет более простой вид:
![]() . (3)
. (3)
При этих условиях нетрудно определить интегральную функцию распределения:
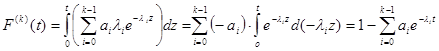 . (4)
. (4)
Математическое ожидание для обобщенного закона Эрланга может быть получено с учетом его свойств и определения потока Эрланга:
![]() . (5)
. (5)
Рассуждая аналогично, получим значение дисперсии для обобщенного закона Эрланга:
![]() . (6)
. (6)
Определение параметров обобщенного закона Эрланга по экспериментальным данным
Параметры обобщенного закона Эрланга авторы предлагают определять с помощью метода моментов, то есть, приравняв теоретические и эмпирические значения математического ожидания и дисперсии.
Пусть ![]() , где
, где ![]() – выборочная средняя случайной величины
– выборочная средняя случайной величины ![]() – интервалов между следующими подряд по одной полосе автомобилями;
– интервалов между следующими подряд по одной полосе автомобилями; ![]() – выборочная дисперсия случайной величины
– выборочная дисперсия случайной величины ![]() . Параметр
. Параметр ![]() – целое число, большее
– целое число, большее ![]() .
.
Экспериментальные исследования авторов показали, что значение ![]() для случайной величины
для случайной величины ![]() не превышает четырех.
не превышает четырех.
Пусть ![]() . В этом случае необходимо определить два неизвестных параметра:
. В этом случае необходимо определить два неизвестных параметра: ![]() и
и ![]() .
.
При ![]() .
.
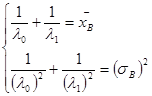
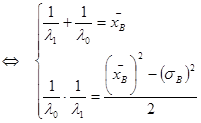 .
.
Обозначим ![]() , тогда
, тогда 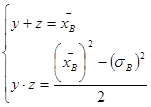 ;
;
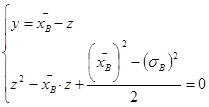
Переменная ![]() является решением квадратного уравнения:
является решением квадратного уравнения:
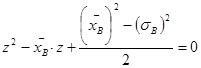 ;
;
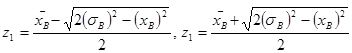 .
.
Таким образом, при условии ![]() значения параметров:
значения параметров:
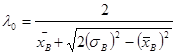 ,
, 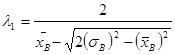 . (7)
. (7)
Найдем отношение ![]() . Введем обозначение:
. Введем обозначение: 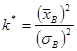 , тогда:
, тогда:
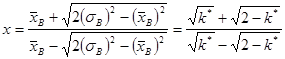 .
.
Неравенство ![]() равносильно следующему:
равносильно следующему: ![]() .
.
Последнее условие как раз и гарантирует наличие действительных значений параметров ![]() .
.
При ![]() . Пусть
. Пусть ![]() , тогда
, тогда
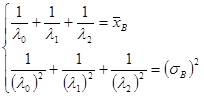
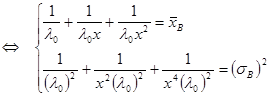
После элементарных преобразований:
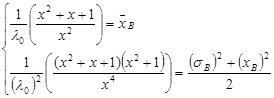 .
.
Возведем первое уравнение в квадрат и разделим первое уравнение на второе. После упрощения получим квадратное уравнение:
![]() .
.
При ![]() корнями уравнения являются:
корнями уравнения являются:
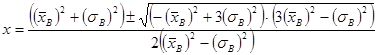 , (8)
, (8)
Учтем обозначение 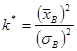 , тогда
, тогда
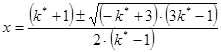 , при
, при ![]() .
.
Условие ![]() гарантирует наличие действительных корней.
гарантирует наличие действительных корней.
После этого находим параметр ![]() :
:
![]() . (9)
. (9)
При ![]() . Пусть
. Пусть ![]() .
.
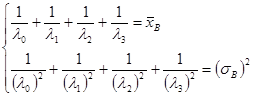
Составим систему уравнений с двумя неизвестными параметрами ![]() и
и ![]() .
.
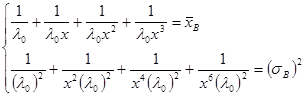
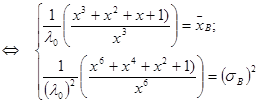
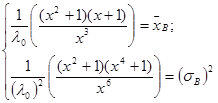
Возведем первое уравнение в квадрат и разделим первое уравнение на второе. После элементарных преобразований получим:
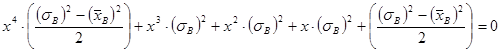 .
.
Это уравнение четвертой степени с симметричными коэффициентами, сводится к квадратному с помощью замены переменной: ![]()
![]() . Следовательно:
. Следовательно:
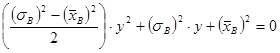
При условии ![]() положительным решением уравнения является:
положительным решением уравнения является:
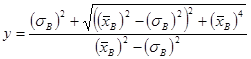 . (10)
. (10)
Тогда:
![]() ;
; ![]() . (11)
. (11)
Учитывая, что ![]() , то есть
, то есть ![]() , найдем условие, гарантирующее наличие действительных значений переменной
, найдем условие, гарантирующее наличие действительных значений переменной ![]() :
:
![]()
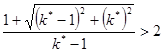 ,
, ![]() .
.
При ![]() неравенство выполнено. При
неравенство выполнено. При ![]() :
:
![]() ,
, ![]() ,
, 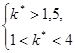 .
.
Таким образом, условие ![]() гарантирует наличие действительных значений переменной
гарантирует наличие действительных значений переменной ![]() .
.
Отметим, что если ![]() – целое число, то для всех
– целое число, то для всех ![]() значение
значение ![]() , а, следовательно, все
, а, следовательно, все ![]() совпадают. Таким образом, получим специальное распределение Эрланга, подробно рассмотренное в работах [5,6].
совпадают. Таким образом, получим специальное распределение Эрланга, подробно рассмотренное в работах [5,6].
Алгоритм проверки гипотезы о виде распределения интервалов по времени по обобщенному закону Эрланга
Адекватность гипотезы о распределении интервалов между автотранспортными средствами по обобщенному закону Эрланга можно проверить по следующему алгоритму:
1) при помощи эксперимента получить зависимость между ![]() – интервалом (по времени) между двумя последовательными прибытиями автомобилей, двигающихся в данном направлении, и количеством ni таких интервалов, появившихся в результате эксперимента;
– интервалом (по времени) между двумя последовательными прибытиями автомобилей, двигающихся в данном направлении, и количеством ni таких интервалов, появившихся в результате эксперимента;
2) вычислить эмпирические моменты:
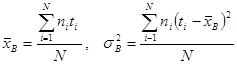 , где
, где ![]() – объем выборки.
– объем выборки.
3) найти вероятность pi попадания случайной величины ![]() в каждый интервал
в каждый интервал ![]() по формуле:
по формуле:
![]() .
.
Тогда теоретическое число значений, попавших в интервал ![]() , рассчитывается по формуле:
, рассчитывается по формуле:
![]() .
.
4) в качестве меры расхождения эмпирических частот и теоретических используется критерий Пирсона:
![]() ( 12)
( 12)
с (L – 3) степенями свободы.
Также можно использовать критерий Романовского:
![]() , (13)
, (13)
где К – число разрядов. Если R < 3, то сходимость считается хорошей.
Заключение
Авторами разработана математическая модель транспортной сети, в которой поток на дугах графа задан как функция плотности распределения интервалов по времени между автотранспортными средствами; выведено аналитическое задание функции транспортных затрат при условии справедливости гипотезы о распределении интервалов по времени по обобщенному закону Эрланга. В данной работе приведен метод определения параметров для работы с вышеуказанной моделью.
Работа выполнена при поддержке РФФИ, проект р-юг-а-13-08-96502.
Рецензенты:
Атрощенко В.А., д.т.н., профессор, декан факультета компьютерных технологий ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.
Видовский Л.А., д.т.н., профессор, заведующий кафедрой вычислительной техники и автоматизированных систем управления ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.
Библиографическая ссылка
Наумова Н.А., Данович Л.М., Данович Ю.И. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ОБОБЩЕННОГО ЗАКОНА ЭРЛАНГА ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ ПРИ ИЗУЧЕНИИ ТРАНСПОРТНЫХ ПОТОКОВ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10045 (дата обращения: 16.02.2026).



