Введение
Необходимость постоянного повышения эффективности радиоэлектронных систем (РЭС) обуславливает требования по обеспечению более высокой стабильности частоты генераторного оборудования [1–7]. Кроме того, постоянный рост требований к стабильности частоты генераторного оборудования связан с непрерывным увеличением количества работающих в пределах одного диапазона РЭС.
Наиболее широкое распространение в современных РЭС находит использование высокостабильных генераторов или методов стабилизации частоты на основе измерения с последующей компенсацией уходов частоты и фазы стабилизируемых колебаний (ЧАПЧ и ФАПЧ) [2, 8, 15]. В то же время в [6] рассматривается принципиально отличающийся статистический метод стабилизации частот генераторов. Однако полученные для этого метода оценки, определяющие повышение стабильности частот генераторного оборудования, относятся к наиболее простому случаю, когда отклонение частоты генератора на интервале измерений является постоянным. Однако в реальных РЭС отклонение частот генераторов даже на малых интервалах времени может изменяться, что связано с рядом факторов и проявляется в виде фазовых шумов. В связи с этим стабилизацию частоты генераторов необходимо рассматривать как нестационарный процесс даже в пределах измерительного интервала.
Цель статьи
Определение оптимальной длительности временного интервала измерений с учетом нестационарности процесса отклонения частот генераторов, обеспечивающей минимум среднеквадратического отклонения частоты генератора от заданной на интервале измерений.
Постановка задачи
Пусть имеется, как предложено в [3], система 
независимо функционирующих генераторов. С учетом нестационарности процесса опишем частоты генераторов на интервале измерений следующими зависимостями:
,
. (1)
В соотношении (1) 
– частота 
-го генератора в середине интервала измерений, 
– длительность интервала измерений. Коэффициенты представленного ряда (1) принимают случайные значения, имеющие нормальный характер распределения. При этом можно считать, что 
, 
, а дисперсии данных коэффициентов 
, 
являются известными.
Оценка отклонения частот
Введем понятие среднего отклонения частоты -го генератора на интервале измерений, определяемого как:
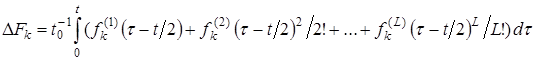, (2)
где 
– номинальная длительность интервала измерений.
Повторяя выкладки, выполненные в [3, 4], получим значение среднего отклонения частоты -го генератора от номинального значения в виде:
. (3)
Несложно заметить, что если в ряде (1) ограничиться только первым членом , то при условии постоянного значения частоты 
соотношение (3) полностью совпадает с выражением (2) из работ [3, 4]. Оценка нестабильности временного интервала 
, полученная там же, определяется следующим образом:
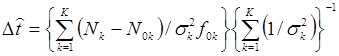. (4)
Таким образом, оценка отклонения частоты -го генератора от среднего значения частоты на интервале измерений может быть записана с использованием соотношения:
. (5)
Данное выражение показывает, что предположение о постоянной величине отклонения частоты на интервале измерений приводит к методической ошибке, равной разности действительного отклонения частоты от номинального значения в конце временного интервала измерений и полученной оценке среднего отклонения частоты. Величина данной ошибки равна:
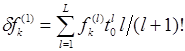. (6)
Минимизация составляющей 
, как следует из физических соображений и формулы (6), связана с уменьшением длительности временного интервала измерений. Однако в то же время из-за ошибок округления при подсчете числа импульсов 
, формируемых -м генератором в течение интервала измерений, возникает вторая составляющая методической ошибки. Величина данной составляющей ошибки равна:
. (7)
Таким образом, с учетом соотношений (6) и (7) полное значение методической ошибки определения отклонения частоты генератора равно:
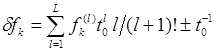. (8)
Проанализируем статистические характеристики получаемых значений методической ошибки 
. С учетом результатов работы [2, 13] можно, опуская промежуточные выкладки, сразу записать:
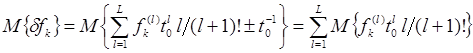. (9)
При сделанных ранее предположениях о значениях математических ожиданий коэффициентов ряда (1) и их некоррелированности из выражения (4) следует, что 
. Таким образом, среднее значение методической ошибки равно нулю. Дисперсия случайных значений методической ошибки определяется выражением:
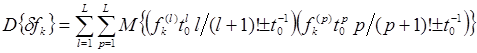. (10)
В случае статистической независимости коэффициентов из ряда (1) выражение (10) упрощается и принимает вид:
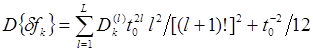. (11)
Минимальное значение дисперсии методической ошибки определяется условием:
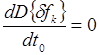. (12)
Опуская несложные преобразования, получаем уравнение для определения длительности временного интервала измерений, обеспечивающего минимум методической ошибки измерений:
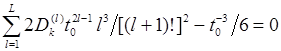. (13)
Единственность решения данного уравнения определяется положительностью всех коэффициентов, стоящих под знаком суммы. Решение данного уравнения может быть легко получено с использованием известных численных методов, например, методом Ньютона [7]. В качестве начального приближения с учетом монотонности функции из (13) можно выбрать значение 
.
Заключение
Приведенные в статье результаты являются дальнейшим развитием метода определения отклонений частот генераторов от номинальных значений, с использованием статистической взаимосвязи параметров одновременно измеряемых отклонений фаз колебаний в совокупности генераторов. Получено уравнение для выбора длительности временного интервала измерений, при котором величина среднеквадратического отклонения частоты каждого генератора минимальна.
Рецензенты:
Костоглотов Андрей Александрович, доктор технических наук, профессор, ведущий научный сотрудник ФГУП «Ростовский-на-Дону научно-исследовательский институт радиосвязи» Федеральный научно-производственный центр, г. Ростов-на-Дону.
Погорелов Вадим Алексеевич, доктор технических наук, доцент, ведущий научный сотрудник ФГУП «Ростовский-на-Дону научно-исследовательский институт радиосвязи» Федеральный научно-производственный центр, г. Ростов-на-Дону.