В процессе рудоподготовки горные породы проходят несколько стадий: предварительное обогащение крупных кусков, дробление, измельчение и классификацию.
Классификация материала по крупности производится с помощью грохотов, в которых разделение частиц горных пород на классы происходит благодаря просеиванию через одно или несколько сит. По характеру движения просеивающей поверхности грохоты могут быть: неподвижными (колосниковыми), плоскими качающимися, вращающимися (барабанными), полувибрационными и вибрационными. Наиболее распространенными на сегодняшний день являются вибрационные грохоты, эффективность которых может достигать 97% [1]. На эффективность разделения влияют, прежде всего, конструктивные и технологические особенности грохота: угол наклона рабочей поверхности, амплитуда, частота и направление вибраций, высота подачи материала, а также нагрузка на просеивающую поверхность. Опытным путем подобрать данные параметры довольно сложно и дорого, поэтому необходима разработка математической модели процесса разделения на основе анализа движения частиц горных пород относительно вибрирующей поверхности.
В работе [3] приведены уравнения движения частицы горной породы относительно пассивного грохота, позволяющие выбрать наилучший угол наклона неподвижной просеивающей поверхности. Показано, что вероятность просеивания при повторных ударах с увеличением угла наклона уменьшается, а наиболее эффективным расположением просеивающей поверхности является такое, при котором этот угол соответствует углу трения пары материал прутка сита – горная порода. С этой точки зрения пассивный грохот должен быть слабонаклонным (угол наклона 6-8°).
Сито активного грохота, как правило, совершает колебания определенной амплитуды и частоты, направления которых составляют с ним некоторый угол. На рис. 1 показано расположение подвижной системы координат, связанной с вибрирующим ситом (ось x направлена вдоль плоскости сита, ось y – перпендикулярно к нему).
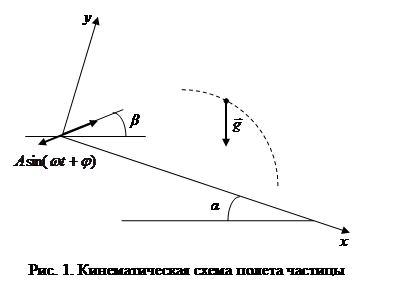
Пренебрегая сопротивлением движению, считаем, что абсолютное ускорение падающей частицы равно 
, а сито совершает свободные гармонические колебания по закону 
(A – амплитуда колебаний, ω – частота, φ – начальная фаза).
В соответствии с кинематической схемой, приведенной на рис. 1, уравнения относительного движения частицы горной породы в дифференциальной форме имеют вид:
|
|
(1) |
где α – угол наклона сита грохота, угол β определяет направление его колебаний.
Интегрируя уравнения (1), получим:
|
|
(2) |
|
|
(3) |
Траектория относительного движения частицы рассчитывается согласно формулам (3) для нулевой начальной скорости при 
. Расчет ведется с небольшим шагом по времени 
до момента времени 
, при котором 
. В точке с абсциссой 
происходит удар о поверхность сита. Проекции скорости 
частицы горной породы в этот момент времени определяются по формулам (2), как 
. Для определения скорости частицы 
непосредственно после удара о сито в векторном виде применяется основная теорема динамики при ударе – теорема об изменении количества движения [2]:
 ,
|
(4) |
где 
– масса частицы, 
и 
– нормальная и касательная составляющие ударного импульса. В проекциях на оси подвижной системы координат это уравнение имеет вид:
|
|
(5) |
При этом касательная составляющая направлена вдоль оси 
противоположно проекции относительной скорости 
. В соответствии с гипотезами Ньютона и Рауса [2] величина проекции составляющей ударного импульса может быть определена в виде
|
|
(6) |
,
где 
– коэффициент трения скольжения при ударе, а проекция скорости частицы после удара на нормаль (ось 
) равна
|
|
(7) |
,
где 
– коэффициент восстановления.
После подстановки выражений (6) и (7) в уравнения (5) получим величины проекций скорости частицы после удара:
|
|
(8) |
,
Дальнейшее движение частицы вновь подчиняется уравнениям (1)-(3), в которых 
Чередование периодов свободного полета частиц и ударов о поверхность сита происходит до момента просеивания частицы через его ячейки при соответствующих размерах частицы или до вылета частицы из рабочей зоны грохота.
Для численного и графического моделирования движения частицы относительно просеивающей поверхности активного грохота, а также статистического анализа результатов многократного моделирования полёта частицы при различных параметрах закона колебаний и случайных значениях фрикционных характеристик частицы в момент удара (моделирование неоднородности породы) разрабатывается вычислительная программа. В программе предусматривается возможность включения режима колебания частицы без просеивания сквозь рабочую поверхность грохота. Этот режим позволит для каждого набора значений параметров закона колебаний рабочей поверхности выполнить наперёд заданное количество численных экспериментов (исход каждого из которых не является детерминированным в силу случайности параметров самой просеиваемой частицы). Задавшись критерием оптимальности – минимальный разброс точек удара частицы вокруг центра просеивающей поверхности – можем отобрать такую совокупность параметров колебаний, которая обеспечит наибольшее число ударов вблизи центра решётки, что в свою очередь увеличивает вероятность просеивания частицы сквозь прутья решётки и снижает риск ухода частицы за просеивающую поверхность рабочего органа.
На рис. 2 приведён пример траектории полёта частицы на подвижной поверхности грохота, полученной с помощью описанной программы.
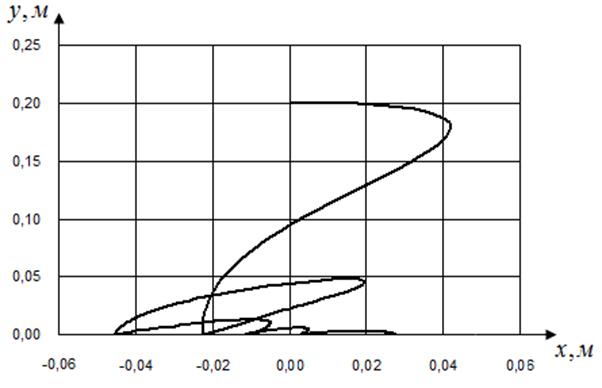
Рис. 2. Траектория полёта частицы в активном грохоте
Частица была свободно отпущена над центром просеивающей поверхности на высоте 0,2 м. Рабочая поверхность грохота наклонена на 5° к горизонтали. Угол между направлением колебаний и положением просеивающей поверхности принят равным нулю. Круговая частота рабочего органа – 23 Гц, амплитуда колебаний – 0,04 м, начальная фаза – 0°. Моделирование 5 ударов частицы о рабочую поверхность выполнено для фиксированных усреднённых параметров: коэффициент трения при ударе 0,1; коэффициент восстановления при ударе 0,46.
Рецензенты:
Герц Эдуард Федорович, доктор технических наук, профессор, декан лесоинженерного факультета ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург.
Готлиб Борис Михайлович, доктор технических наук, профессор, заведующий кафедрой мехатроники ФГБОУ ВПО «Уральский государственный университет путей сообщения», г. Екатеринбург.
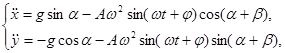
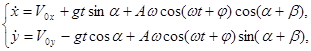
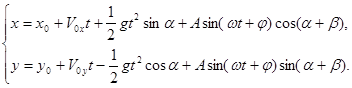
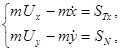
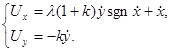