Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Для банков важным вопросом является оптимизация стоимости владения сетями самообслуживания. Одной из больших статей расходов являются затраты на инкассацию. Для оптимизации надо уметь моделировать процесс движения наличности в банкомате, что даст возможность прогнозировать дневной расход, необходимый для обеспечения банкоматных операций. Ежедневный расход наличности можно рассматривать как временной ряд. Метод прогнозирования для временного ряда зависит, в том числе, от персистентности ряда. Целью настоящей работы являлась попытка применения показателя Хёрста для оценки персистентности ряда среднедневных снятий наличности в банкоматах.

Прогнозирование объема инкассации

В литературе отмечены самые разнообразные подходы к решению задачи моделирования процесса инкассации [1, 2, 3, 5]. Следует отметить, что почти все подходы опираются на исследование вероятностной природы процесса расхода и прихода денежных средств, необходимо уметь их прогнозировать.

В работе [2] для того чтобы производить оптимальное планирование инкассации, необходимо для каждого банкомата определить характерные для этого банкомата особенности, такие как:

· Среднесуточный расход денежных средств для данного банкомата.

· Разницу между максимальным суточным расходом и среднесуточным расходом.

· Наличие дней с нулевым расходом.

На основании данных характеристик можно классифицировать банкоматы и на основе данной классификации производить наиболее точное планирование инкассаций. В [2] выделяются 3 основных типа банкоматов: зарплатные, уличные банкоматы и банкоматы с ограниченным доступом.

· Зарплатный. На банкоматах такого типа снятие основных денежных средств происходит примерно за 1–2 дня, в момент получения зарплаты сотрудниками. На основании статистики банкомата можно определить необходимую сумму для инкассации, путем расчета среднемесячного съема денежных средств.

· Уличные банкоматы. Данный тип банкоматов располагают в местах скопления людей, например, входы/выходы метро, гипермаркеты, и просто на оживленной улице. Учитывая характер спроса, можно рассчитать среднесуточный объем снятия наличности.

· Банкоматы, с ограниченным доступом по дням недели. Такой тип банкоматов может использоваться в магазинах розничной торговли, офисах и любых объектах, доступ к которым ограничен, например, в выходные и праздничные дни. Расчетная сумма инкассации будет складываться из среднесуточного съема средств с банкомата, а дата благоприятной инкассации определяется днями низкой активности банкоматов.

Одна из важнейших задач анализа и прогнозирования движения денег в банкоматных системах состоит в определении объема инкассации.

Обоснование средств, оптимальных для инкассации в заданный период, определяется исходя из положений теории запасов и вычисляется по формуле [2]:

Sk= ,

где Sk – сумма инкассации, s – сумма, запрашиваемая с k-ого банкомата за сутки, К – банковский процент (процент, под который банк мог бы заложить средства, пролеживающие в банкомате), V – стоимость одной инкассации, T – число дней в году. Заметим, что итоговая сумма инкассации не зависит от величины времени, на которую происходит расчет, на квартал или на год, это значит, что сумма инкассации для фиксированного банкомата, при условии довольно большой статистики, не зависит от временного промежутка расчета. Таким образом, полученная формула будет показывать оптимальное значение инкассации для заданного периода, с максимальной экономией средств для банка.

Моделирование временного ряда снятий наличности

В работе [1] для проверки и уточнения полученных теоретических выражений было осуществлено статистическое моделирование процесса функционирования банкомата. Моделировались как поток клиентов, так и денежный поток. Статистическое моделирование проводилось также для того, чтобы учесть особенности реальных стохастических характеристик потока клиентов и денежного потока, которые, в общем случае, как было показано в первой главе, существенно зависят как от времени суток, так и от дня недели и месяца. Поэтому при моделировании потока клиентов предполагалось, что поток пуассоновский, но его интенсивность зависит от времени. Длительность обслуживания клиентов моделировалась логнормальным распределением, а величина денежной суммы операции – гамма-распределением.

В статистических моделях ежедневный расход наличности можно рассматривать как временной ряд. Дискретный временной ряд Z1, Z2, Z3..., ZN-1, ZN может быть моделирован различными методами.

На практике применяются методы, основанные на сглаживании (методы Хольта, Винтерса) [3] и авторегрессионные методики Бокса – Дженкинса (модели ARIMA, SARIMA) [6]. При этом прогнозирование временного ряда выполняется на основании информации, которая содержится в исторических данных конкретного ряда.

Для представления модели SARIMA используется сезонные и несезонные параметры авторегрессии, разностных операторов и операторов скользящего среднего [6].

Дискретный временной ряд также может быть моделирован методом Хольта –Винтерса на основе экспоненциального сглаживания [3]. Метод использует параметр сезонности и параметры экспоненциального сглаживания.

Эти модели также хорошо подходят для анализа временных рядов, которые по своему характеру являются персистентными (трендовыми), однако персистентность ряда требует проверки.

Персистентность – долгосрочное статистическое свойство расхода наличных, согласно которому за периодами значительного расхода, как правило, следуют другие периоды высокого расхода и аналогично после периодов незначительного расхода следуют периоды незначительного расхода..

Для определения персистентности временного ряда используется показатель Хёрста, связывающий объем ряда N, его размах R и среднеквадратичное отклонение S.

Показатель Херста

В начале ХХ века британский гидролог Гарольд Эдвин Херст (1880–1978) решал задачу контроля уровня воды в водохранилище. Для калибровки этих временных измерений Херст ввел безразмерное отношение посредством деления размаха на стандартное отклонение наблюдений. Этот способ анализа стал называться методом нормированного размаха (R/S-анализ). Показатель Херста был использован в других областях, таких как финансы и кардиология.

Вычисление показателя Хёрста производится по следующей схеме. Рассмотрим временной ряд снятия наличности Zt, t = 1, ..., N и подвыборки Z1, … , Zn с n ≤ N, следуя [4, 6] сначала вычисляются отклонения от среднего значения по подвыборке и накопленные частичные суммы отклонений от среднего

Si*=S(i-1)*+(Zi-n) )

где S0* = 0 и n является выборочным средним значением. Размах R и нормированный размах R** зададим формулами:

Rn*=max(0,S1*,S2*,…,Sn*)-min(0,S1*,S2*,…,Sn*)

Далее мы нормируем размах делением на стандартное отклонение sn, которое вычисляется по n значениям.

Rn**=(Rn*)⁄sn

в которых sn это выборочное стандартное отклонение.

Хёрст показал, что Rn**=(k×nH), где k константа.

Усредним Rn** по всем подвыборкам длины n и логарифмируем. Строим на основании полученных данных график путём линейной регрессии. По графику прямой аппроксимирующей зависимость log(Rn**) от log(n/2) находим наклон. Тангенс угла наклона и является показателем Хёрста H.

Для случайных блужданий согласно статистической механике H = 0,5. Для большого числа природных временных рядов, 0,5 < H < 1 .Тот факт, что показатель, H в уравнении не согласуются с теорией, основанной на чисто случайном процессе, было названо явление Хёрста.

Результаты Хёрста означают, что для данной величины n размер суммы должен был бы быть больше, чем сумма чисто случайных последовательных слагаемых [4,6].

Имеется три диапазона значений показателя Хёрста:

H=0,5; 0≤H<0,5; 0,5<H≤1.

H=0,5 – указывает на случайный ряд. События случайны и не коррелированы. Настоящее не влияет на будущее. В курсах статистики говорится, что природа следует нормальному распределению. Открытие Хёрста это положение опровергает. Показатель Н, как правило, бывает больше 0,5, а вероятностные распределения не являются нормальными.

0≤H<0,5 – данный диапазон соответствует антиперсистентным, или эргодическим, рядам. Такой тип системы часто называют «возврат к среднему». Если система демонстрирует рост в предыдущий период, то, скорее всего в следующем периоде начнется спад. И наоборот, если шло снижение, то вероятен близкий подъем.

0,5<H≤1 – наблюдаем персистентные, или трендоустойчивые ряды. Если ряд возрастает (убывает) в предыдущий период, то, вероятно, что он будет сохранять эту тенденцию какое-то время в будущем. Чем ближе Н к 0,5 – тем более зашумлен ряд и тем менее выражен его тренд. Персистентный ряд – это обобщенное броуновское движение, или смещенные случайные блуждания. Сила этого смещения зависит от того, насколько Н больше 0,5.

Модель зависимости log(Rn**) от log(n/2)

Microsoft Excel позволяет строить модели, в которых используются весьма сложные вычисления, деловая графика, запросы к базам данных, и всё это может управляться программой, написанной на VisualBasic.

Данные по каждому банкомату могут быть помещены диапазон на лист Microsoft Excel.

В рамках моделирования на Microsoft Excel достаточно просто построить модель, в которой это среднее будет считаться для всего диапазона, его половин, четвертей и т. д. Для этого достаточно воспользоваться присутствием в Microsoft Excel возможности строить переменные ссылки. Переменные ссылки можно, например, строить с использованием функции ИНДЕКС. Аналогично, вырезать скользящее окно шириной F$1 из столбца С позволит выражение, использующее функцию ДВССЫЛ.

Однако подобная методика требует, чтобы размерность вектора исходных данных составляла степень двойки, что не всегда возможно в реальном эксперименте. Кроме того, слишком короткие интервалы (<10) приводят к завышению значений коэффициента Хёрста. Разбиение же вектора исходных данных на интервалы, длина которых не является делителем размерности вектора, приводит к появлению остаточных данных, которые приходится отбрасывать.

Результаты эксперимента

Основную сложность в исследовании составляет сложность получения исходных данных. Банки неохотно предоставляют данные по функционированию сетей банкоматов. В нашем распоряжении были данные по снятиям наличности из банкоматов, использованные для типизации банкоматов [2,3].

Для каждого банкомата были построены зависимости log(Rn**) от log(n/2) в двойном логарифмическом масштабе, см. рисунок 1.

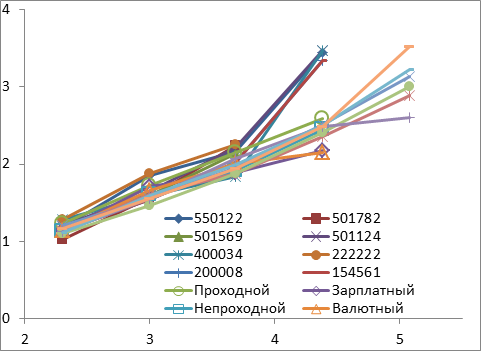
Рисунок 1. Зависимости log(Rn**) от log(n/2) в двойном логарифмическом масштабе

Затем для каждого банкомата построено уравнение линейной регрессии y=ax+b. Силу зависимости оценим, используя коэффициент детерминированности r2. Параметры линеаризации каждого графика представлены в таблице 1.

Таблица 1. Параметры линеаризации

Для банкомата, для которого известно, что он является зарплатным банкоматом, полученное значение показателя Хёрста выходит за 95 % доверительный интервал. Аналогичный результат получен и для валютного банкомата.

Выводы

Проведенный эксперимент показывает, что показатель Хёрста позволяет классифицировать банкоматы. Ряд снятий является чисто случайным для банкоматов зарплатного и валютного вида и является персистентным для остальных банкоматов. Для того чтобы получить статистически значимые значения показателя Хёрста для банкоматов различных типов, необходимо провести расчёты с увеличенным количеством банкоматов.

Рецензенты:

Загребаев А. М., д.ф.-м.н., профессор, заведующий кафедрой «Кибернетика» № 22, Министерство образования и науки Российской Федерации, Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ» (НИЯУ МИФИ), г. Москва.

Гусева А. И., д.т.н., профессор, профессор кафедры «Экономика и менеджмент в промышленности», Министерство образования и науки Российской Федерации, Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет «МИФИ» (НИЯУ МИФИ), г. Москва.